- Programming Example: Moving to a DL Framework
- The Problem of Saturated Neurons and Vanishing Gradients
- Initialization and Normalization Techniques to Avoid Saturated Neurons
- Cross-Entropy Loss Function to Mitigate Effect of Saturated Output Neurons
- Different Activation Functions to Avoid Vanishing Gradient in Hidden Layers
- Variations on Gradient Descent to Improve Learning
- Experiment: Tweaking Network and Learning Parameters
- Hyperparameter Tuning and Cross-Validation
- Concluding Remarks on the Path Toward Deep Learning
Different Activation Functions to Avoid Vanishing Gradient in Hidden Layers
The previous section showed how we can solve the problem of saturated neurons in the output layer by choosing a different loss function. However, this does not help for the hidden layers. The hidden neurons can still be saturated, resulting in derivatives close to 0 and vanishing gradients. At this point, you may wonder if we are solving the problem or just fighting symptoms. We have modified (standardized) the input data, used elaborate techniques to initialize the weights based on the number of inputs and outputs, and changed our loss function to accommodate the behavior of our activation function. Could it be that the activation function itself is the cause of the problem?
How did we end up with the tanh and logistic sigmoid functions as activation functions anyway? We started with early neuron models from McCulloch and Pitts (1943) and Rosenblatt (1958) that were both binary in nature. Then Rumelhart, Hinton, and Williams (1986) added the constraint that the activation function needs to be differentiable, and we switched to the tanh and logistic sigmoid functions. These functions kind of look like the sign function yet are still differentiable, but what good is a differentiable function in our algorithm if its derivative is 0 anyway?
Based on this discussion, it makes sense to explore alternative activation functions. One such attempt is shown in Figure 5-8, where we have complicated the activation function further by adding a linear term 0.2*x to the output to prevent the derivative from approaching 0.
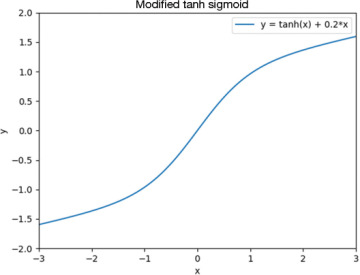
FIGURE 5-8 Modified tanh function with an added linear term
Although this function might well do the trick, it turns out that there is no good reason to overcomplicate things, so we do not need to use this function. We remember from the charts in the previous section that a derivative of 0 was a problem only in one direction because, in the other direction, the output value already matched the ground truth anyway. In other words, it is fine with a derivative of 0 on one side of the chart. Based on this reasoning, we can consider the rectified linear unit (ReLU) activation function in Figure 5-9, which has been shown to work for neural networks (Glorot, Bordes, and Bengio, 2011).
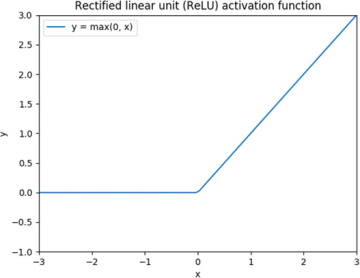
FIGURE 5-9 Rectified linear unit (ReLU) activation function
Now, a fair question is how this function can possibly be used after our entire obsession with differentiable functions. The function in Figure 5-9 is not differentiable at x = 0. However, this does not present a big problem. It is true that from a mathematical point of view, the function is not differentiable in that one point, but nothing prevents us from just defining the derivative as 1 in that point and then trivially using it in our backpropagation algorithm implementation. The key issue to avoid is a function with a discontinuity, like the sign function. Can we simply remove the kink in the line altogether and use y = x as an activation function? The answer is that this does not work. If you do the calculations, you will discover that this will let you collapse the entire network into a linear function and, as we saw in Chapter 1, “The Rosenblatt Perceptron,” a linear function (like the perceptron) has severe limitations. It is even common to refer to the activation function as a nonlinearity, which stresses how important it is to not pick a linear function as an activation function.
An obvious benefit with the ReLU function is that it is cheap to compute. The implementation involves testing only whether the input value is less than 0, and if so, it is set to 0. A potential problem with the ReLU function is when a neuron starts off as being saturated in one direction due to a combination of how the weights and inputs happen to interact. Then that neuron will not participate in the network at all because its derivative is 0. In this situation, the neuron is said to be dead. One way to look at this is that using ReLUs gives the network the ability to remove certain connections altogether, and it thereby builds its own network topology, but it could also be that it accidentally kills neurons that could be useful if they had not happened to die. Figure 5-10 shows a variation of the ReLU function known as leaky ReLU, which is defined so its derivative is never 0.
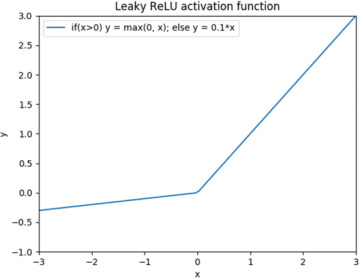
FIGURE 5-10 Leaky rectified linear unit (ReLU) activation function
All in all, the number of activation functions we can think of is close to unlimited, and many of them work equally well. Figure 5-11 shows a number of important activation functions that we should add to our toolbox. We have already seen tanh, ReLU, and leaky ReLU (Xu, Wang, et al., 2015). We now add the softplus function (Dugas et al., 2001), the exponential linear unit also known as elu (Shah et al., 2016), and the maxout function (Goodfellow et al., 2013). The maxout function is a generalization of the ReLU function in which, instead of taking the max value of just two lines (a horizontal line and a line with positive slope), it takes the max value of an arbitrary number of lines. In our example, we use three lines, one with a negative slope, one that is horizontal, and one with a positive slope.
All of these activation functions except for tanh should be effective at fighting vanishing gradients when used as hidden units. There are also some alternatives to the logistic sigmoid function for the output units, but we save that for Chapter 6.
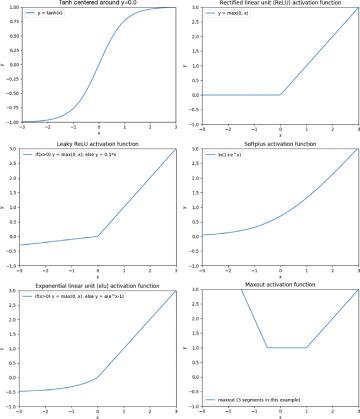
FIGURE 5-11 Important activation functions for hidden neurons. Top row: tanh, ReLU. Middle row: leaky ReLU, softplut. Bottom row: elu, maxout.
We saw previously how we can choose tanh as an activation function for the neurons in a layer in TensorFlow, also shown in Code Snippet 5-10.
Code Snippet 5-10 Setting the Activation Function for a Layer
keras.layers.Dense(25, activation='tanh',
kernel_initializer=initializer,
bias_initializer='zeros'),
If we want a different activation function, we simply replace 'tanh' with one of the other supported functions (e.g., 'sigmoid', 'relu', or 'elu'). We can also omit the activation argument altogether, which results in a layer without an activation function; that is, it will just output the weighted sum of the inputs. We will see an example of this in Chapter 6.
