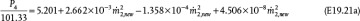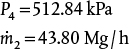- 19.1 Basic Relationships in Fluid Mechanics
- 19.2 Fluid Flow Equipment
- 19.3 Frictional Pipe Flow
- 19.4 Other Flow Situations
- 19.5 Performance of Fluid Flow Equipment
- References
- Short Answer Questions
- Problems
19.5 Performance of Fluid Flow Equipment
In addition to equipment design, the chemical engineer must deal with the performance of existing equipment. The differences between the design problem (also called a rating problem) (a) and the performance problem (b) are illustrated in Figure 19.17. The use of italics indicates the unknowns in the particular problem. In the design problem, the input and the desired output are specified, and the equipment is designed to satisfy those constraints. In the performance problem, the input and equipment are specified, and the output is determined. The performance problem is what is involved in dealing with day-to-day operations in a chemical plant.
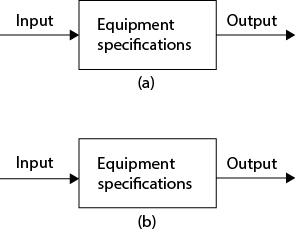
Figure 19.17 Illustrations of (a) Design Problem and (b) Performance Problem (Unknowns Are Indicated by Italics for Each Case)
Several different types of problems in frictional fluid flow using the mechanical energy balance were discussed in Section 19.3. Determining the pump power needed for a given situation is a design problem. Similarly, determining the required pipe diameter is a design problem. On the other hand, determining the flowrate when all equipment is specified is a performance problem, as is determining the pressure change for an existing system.
Suppose it is necessary to increase the capacity of a process without adding new equipment. Logically, all flowrates must increase. This is a performance problem, since the input and equipment are specified, and the output must be determined for each unit in the process. Somewhere in the process, the amount of scale-up needed will be limited due to equipment constraints, and this limiting unit is called a bottleneck. The process of finding a solution that removes the bottleneck is called debottlenecking, which is a performance problem. Similarly, if there is a problem with the output of a process (purity or temperature, for example), the cause of the problem must be determined, which is called troubleshooting.
Returning to the situation in which process capacity must be increased, for the fluid flow component, initially, it may appear that problems similar to those in Section 19.3 must be solved from scratch. However, for many situations, not just in fluid flow, very good approximations can be made with a much simpler analysis.
19.5.1 Base-Case Ratios
The ability to predict changes in a process design or in plant operations is improved by anchoring an analysis to a base case. This calculation tool combines use of fundamental relationships with plant operating data to form a basis for predicting changes in system behavior. As will be seen, it is applicable to problems involving all chemical process units when analytical expressions are available.
For design changes, it is desirable to identify a design proven in practice as the base case. For operating plants, actual data are available and are chosen as the base case. It is important to put this base case into perspective. Assuming that there are no instrument malfunctions and these operating data are correct, then these data represent a real operating point at the time the data were taken. As the plant ages, the effectiveness of process units changes and operations are altered to account for these changes. As a consequence, recent data on plant operations should be used in setting up the base case.
The base-case ratio integrates the “best available” information from the operating plant with design relationships to predict the effect of process changes. It is an important and powerful technique with a wide range of applications. The base-case ratio, X, is defined as the ratio of a new-case system characteristic, x2, to the base-case system characteristic, x1:
Using a base-case ratio often reduces the need for knowing actual values of physical properties (physical properties refer to thermodynamic and transport properties of fluids), equipment, and equipment characteristics. The values identified in the ratios fall into three major groups. They are defined below and applied in Examples 19.15 and 19.16.
Ratios Related to Equipment Sizes (equivalent length, Leq; diameter, D; surface area, A): Assuming that the equipment is not modified, these values are constant, the ratios are unity, and these terms cancel out.
Ratios Related to Physical Properties (such as density, ρ; viscosity, μ): These values can be functions of material composition, temperature, and pressure. Only the functional relationships, not absolute values, are needed. For small changes in composition, temperature, or pressure, the properties often are unchanged, and the ratio is unity and cancels out. An exception to this is gas-phase density.
Ratios Related to Stream Properties: These ratios usually involve velocity, flowrate, concentration, temperature, and pressure.
Using the base-case ratio eliminates the need to know equipment characteristics and reduces the amount of physical property data needed to predict changes in operating systems.
The base-case ratio is a powerful and straightforward tool to analyze and predict process changes. This is illustrated in Example 19.15.
19.5.2 Net Positive Suction Head
There is a significant limitation on pump operation called net positive suction head (NPSH). This is the head that is needed on the pump feed (suction) side to ensure that liquid does not vaporize upon entering the pump. Its origin is as follows. Although the effect of a pump is to raise the pressure of a liquid, frictional losses at the entrance to the pump, between the suction pipe and the internal pump mechanism, cause the liquid pressure to drop upon entering the pump. This means that a minimum pressure exists somewhere within the pump. If the feed liquid is saturated or nearly saturated, the liquid can vaporize upon entering due to this internal pressure drop. This causes formation of vapor bubbles. These bubbles rapidly collapse when exposed to the forces created by the pump mechanism, called cavitation. This process usually results in noisy pump operation and, if it occurs for a period of time, will damage the pump. As a consequence, regulating valves, which lower fluid pressure, are not normally placed in the suction line to a pump.
Pump manufacturers supply NPSH data with a pump, usually in head units. In this book, both head and pressure units are used. The required NPSH, denoted NPSHR, is a function of the square of velocity because it is a frictional loss and because most applications involve turbulent flow. Figure 19.18(a) shows NPSHR and NPSHA curves, which define a region of acceptable pump operation. This is specific to a given liquid. Typical NPSHR values are in the range of 15 to 30 kPa (2-4 psi) for small pumps and can reach 150 kPa (22 psi) for larger pumps. Figure 19.18 also shows curves for NPSHA, the available NPSH, along with the NPSHR curve.
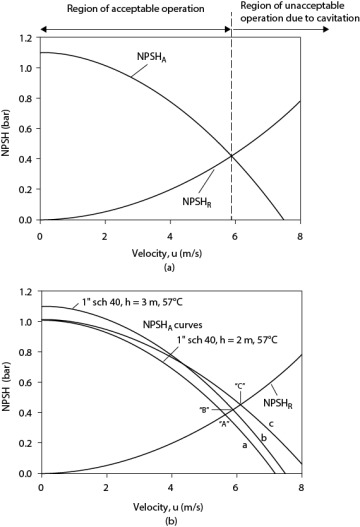
Figure 19.18 (a) NPSHA and NPSHR Curves Showing Region of Feasible Operation; (b) How Physical Parameters Affect Shape of NPSHA Curve
The available NPSHA is defined as
Equation (19.66) means that the available NPSH (NPSHA) is the difference between the inlet pressure, Pinlet, and P*, which is the vapor pressure (bubble-point pressure for a mixture). It is required that NPSHA ≥ NPSHR to avoid cavitation. Cavitation is avoided if operation is to the left of the intersection of the two curves. It is physically possible to operate to the right of the intersection of the two curves, but doing so is not recommended because the pump will be damaged.
All that remains is to calculate or know the pump inlet conditions in order to determine whether sufficient NPSH (NPSHA) is available to equal or exceed the required NPSH (NPSHR). For example, consider the exit stream from a distillation column reboiler, which is saturated liquid. If it is necessary to pump this liquid, cavitation could be a problem. A common solution to this problem is to elevate the column above the pump so that the static pressure increase minus any frictional losses between the column and the pump provides the necessary NPSH to avoid cavitation. This can be done either by elevating the column above ground level using a metal skirt or by placing the pump in a pit below ground level, although pump pits are usually avoided due to safety concerns arising from accumulation of heavier-than-air gases in the pit.
In order to quantify NPSH, consider Figure 19.19, in which material in a storage tank is pumped downstream in a chemical process. This scenario is a very common application of the NPSH concept. For NPSH analysis, the only portion of Figure 19.19 under consideration is between the tank and pump inlet.
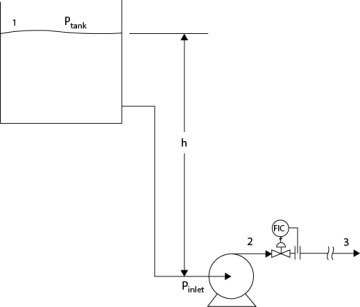
Figure 19.19 Typical Situation for Application of NPSH Principles
From the mechanical energy balance, the pressure at the pump inlet can be calculated to be
which means that the pump inlet pressure is the tank pressure plus the static pressure minus the frictional losses in the suction-side piping. Therefore, by substituting Equation (19.67) into Equation (19.66), the resulting expression for NPSHA is
This is an equation of a concave downward parabola, of the form 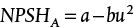 , as illustrated in Figure 19.18(b), Curve a. The intercept is a = Ptank + pgh − P* and b = 2ρfLeq/D. This analysis does not include the kinetic energy term due to the acceleration of the fluid from the tank into the pipe. Rigorously, this term should also be included in the analysis.
, as illustrated in Figure 19.18(b), Curve a. The intercept is a = Ptank + pgh − P* and b = 2ρfLeq/D. This analysis does not include the kinetic energy term due to the acceleration of the fluid from the tank into the pipe. Rigorously, this term should also be included in the analysis.
If NPSHA is insufficient for a particular situation, Equation (19.68) suggests methods to increase the NPSHA:
Decrease the temperature of the liquid at the pump inlet. This decreases the value of the vapor pressure, P*, thereby increasing NPSHA. This increases the intercept of the NPSHA curve while maintaining constant curvature, as illustrated in Figure 19.18(b), Curve b.
Increase the static head. This is accomplished by increasing the value of h in Equation (19.64), thereby increasing NPSHA. As was said earlier, pumps are most often found at lower elevations than the source of the material they are pumping. This increases the intercept of the NPSHA curve while maintaining constant curvature, as illustrated in Figure 19.18(b), Curve b.
Increase the tank pressure. This increases the intercept of the NPSHA curve while maintaining constant curvature, as illustrated in Figure 19.18(b), Curve b.
Increase the diameter of the suction line (feed pipe to pump). This reduces the velocity and the frictional loss term, thereby increasing NPSHA. This decreases the curvature of the NPSHA curve, as illustrated in Figure 19.18(b), Curve c. It is standard practice to have larger-diameter pipes on the suction side of a pump than on the discharge side.
Example 19.17 illustrates how to do NPSH calculations and one of the preceding methods for increasing NPSHA. The other methods are illustrated in problems at the end of the chapter.
19.5.3 Pump and System Curves
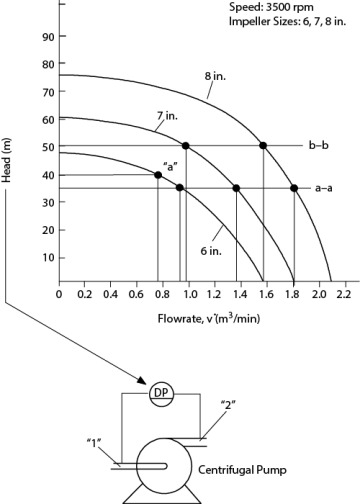
Pumps also have characteristic performance curves, called pump curves. Figure 19.20 illustrates a pump curve for a centrifugal pump. Centrifugal pumps are often called constant head pumps because, over a wide range of volumetric flowrates, the head produced by the pump is approximately constant. Pump manufacturers provide the characteristic curve, usually in head units. For centrifugal pumps, the shape of the curve indicates that although the head remains constant over quite a wide range of flowrates, eventually, as the flowrate continues to increase, the head produced decreases. Pump curves also include power and efficiency curves, both of which change with flowrate and head; however, these are not shown here.
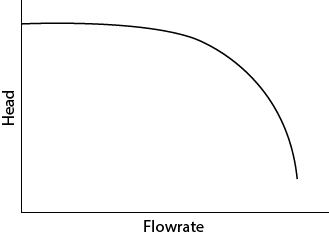
Figure 19.20 Typical Shape of Pump Curve for Centrifugal Pump
For a piping system, a system curve can also be defined. Consider the system as illustrated in Figure 19.21. Location 1 is called the source, and Location 2 is the destination. Location 2 may be distant from Location 1, perhaps at the opposite end of a chemical process and at a different elevation from Location 1. Typical processes have only one pump upstream to supply all pressure needed to overcome pressure losses throughout the process. Therefore, the pressure increase across the pump must be sufficient to overcome all of the losses associated with piping and fittings plus the indicated pressure loss across the control valve. The orifice plate is present to illustrate some type of flowrate measurement, and the flow indicator controller (FIC) illustrates that the measured flowrate is compared to a set point, and deviations from the set point are compensated by adjusting the valve, usually pneumatically. If the flowrate is too large, the valve is partially closed, restricting the flowrate. However, this also increases the frictional pressure loss across the valve, as discussed in Section 19.3.2.
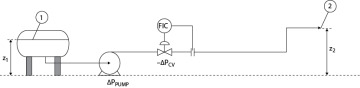
Figure 19.21 Physical Situation for System Curve
The behavior of the system can be quantified by a system curve. The general equation for a chemical process, in terms of pressure, is given by the mechanical energy balance between Points 1 and 2 in Figure 19.21:
where
Equation (19.70) is derived from the mechanical energy balance with only the pressure and friction terms. It is important to remember that Δ represents out-in; therefore, the frictional loss term and the pressure loss across the valve are negative numbers before the included negative sign. The system curve is the right-hand side of Equation (19.69) without the term for the control valve:
Equation (19.71) is a parabola, concave upward, on a plot of pressure increase versus flowrate. It is of the form 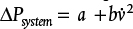 , where a = (P2 − P1) + ρ g(z2 −z1) and
, where a = (P2 − P1) + ρ g(z2 −z1) and 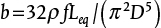 . Since the manufacturer pump curve is usually provided in head units, Equation (19.69) can be rewritten in head units as
. Since the manufacturer pump curve is usually provided in head units, Equation (19.69) can be rewritten in head units as
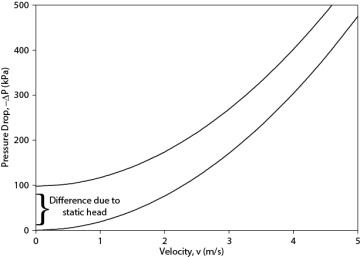
Figure 19.22 illustrates the result if the pump curve and the system curve are plotted on the same graph. The indicated pressure changes demonstrate how the head provided by the pump must equal the desired head increase from source to destination, plus the frictional pressure loss, plus the pressure loss across the control valve, as quantified in Equation (19.69). The process of flowrate regulation is also illustrated in Figure 19.22. If the flowrate is to be reduced, the valve is closed, and the operating point moves to the left. At this lower flowrate, the frictional losses are lower, but the pressure loss across the valve is larger. The opposite is true for a higher flowrate. At the intersection of the two curves, the valve is wide open, and the maximum possible flowrate has been reached. This analysis assumes that the pump is operating at constant speed. For a variable speed pump, the pump curve moves up or down as the speed of rotation of the impeller changes. (Note that this simplified explanation omits the very small pressure drop across a wide-open control valve.) Operation to the right of this point is impossible. It is important not to confuse the meanings of the intersection points on the pump-system curve plot and the NPSH plot.
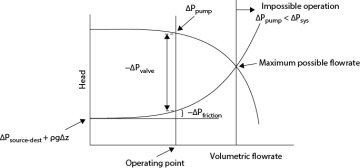
Figure 19.22 Pump (Constant Speed Centrifugal Pump) and System Curve Components
The pump and system curve plot also illustrates the cost of flowrate regulation. The pump must provide sufficient pressure to overcome the losses across the valve over a wide range of flowrates. Additional pump power is required for the possibility of operating at lower flowrates with a very large pressure drop across the valve. In general, this is a small cost for a pump, because the liquid density is high. Variable speed pumps are also available with different pump curves for different speeds. For these, the flowrate is regulated by the rotation speed of the impeller, not by a valve. It is not usually worth the extra cost for small pumps given the low cost of pumping liquids but may be worth considering for larger pumps and flowrates. Pumps with different impeller sizes have different pump curves for each impeller size. However, changing an impeller is not something that can be done while a process is operating.
Pumps (and compressors) are about the only pieces of equipment in a chemical plant with moving parts. Moving parts can fail. Therefore, since pumps are often inexpensive (on the order of $10,000), a backup pump is typically installed in parallel so the plant can continue operating while the primary pump is maintained. Since shutdown and start-up can take days, it makes sense not to shut down a process that generates profit at a rate of thousands of dollars per minute to avoid purchasing a relatively inexpensive backup pump.
The presence of a backup pump can also be exploited if is necessary to scale-up a process. The piping system can be constructed such that the two pumps can operate simultaneously, either in series or in parallel. If the pumps are in series, the head increase doubles at the same flowrate. If the pumps are in parallel, the flowrate doubles at the same head increase. The pump curves for these situations are illustrated in Figure 19.23. The two system curves illustrate the maximum possible scale-up for two different system curves, indicated by the dots. In one case, the parallel configuration provides more scale-up potential, and in the other case, the series configuration provides more scale-up potential. This demonstrates that it is not possible to make any generalizations about which configuration can produce more scale-up. It all depends on the particular system.
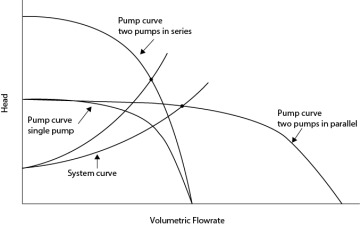
Figure 19.23 Pump and System Curves for Series and Parallel Pumps
Positive-displacement pumps perform differently from centrifugal pumps. They are usually used to produce higher pressure increases than are obtained with centrifugal pumps. The performance characteristics are represented on Figure 19.24(a), and these are sometimes referred to as constant-volume pumps. It can be observed that the flowrate through the pump is almost constant over a wide range of pressure increases, which makes flowrate control using the pressure increase impractical. One method to regulate the flow through a positive-displacement pump is illustrated in Figure 19.24(b). The strategy is to maintain constant flowrate through the pump. By regulating the flow of the recycle stream to maintain constant flowrate through the pump, the downstream flowrate can be regulated independently of the flow through the pump. Therefore, if a higher flow to the process is needed, then the bypass control valve is closed, and vice versa.
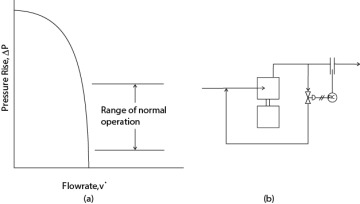
Figure 19.24 (a) Typical Pump Curve for Positive−Displacement Pump and (b) Method for Flowrate Regulation
It is observed from Figure 19.21 and Figure 19.24 that, in both cases, flowrate regulation occurs by adjusting a valve. For regulation of temperature, a valve on a cooling or heating fluid is adjusted. For regulation of concentration, valves on mixing streams are adjusted. This emphasizes the concept that about the only way to regulate anything in a chemical process is to adjust a valve position.
19.5.4 Compressors
19.5.4.1 Compressor Curves
The performance of centrifugal compressors is somewhat analogous to that of centrifugal pumps. A characteristic performance curve, supplied by the manufacturer, defines how the outlet pressure varies with flowrate. However, compressor behavior is far more complex than that for pumps because the fluid is compressible.
Figure 19.25 shows the performance curves for a centrifugal compressor. It is immediately observed that the y-axis is the ratio of the outlet pressure to inlet pressure. This is in contrast to pump curves, which have the difference between these two values on the y-axis. Curves for two different rotation speeds are shown. As with pump curves, curves for power and efficiency are often included but are not shown here. Unlike most pumps, the speed is often varied continuously to control the flowrate because the higher power required in a compressor makes it economical to avoid throttling the outlet as in a centrifugal pump.
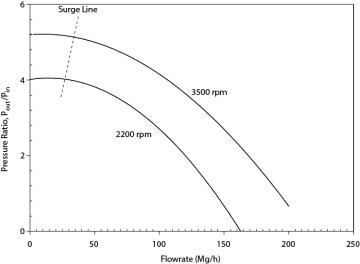
Figure 19.25 Performance Curves for a Centrifugal Compressor
Centrifugal compressor curves are read just like pump curves. At a given flowrate and revolutions per minute, there is one pressure ratio. The pressure ratio decreases as flowrate increases. A unique feature of compressor behavior occurs at low flowrates. It is observed that the pressure ratio increases with decreasing flowrate, reaches a maximum, and then decreases with decreasing flowrate. The locus of maxima is called the surge line. For safety reasons, compressors are operated to the right of the surge line. The surge line is significant for the following reason. Imagine the compressor is operating at a high flowrate and the flowrate is lowered continuously, causing a higher outlet pressure. At some point, the surge line is crossed, lowering the pressure ratio. This means that downstream fluid is at a higher pressure than upstream fluid, causing a backflow. These flow irregularities can severely damage the compressor mechanism, even causing the compressor to vibrate or surge (hence the origin of the term). Severe surging has been known to cause compressors to become detached from the supports keeping them stationary and literally to fly apart, causing great damage. Therefore, the surge line is considered a limiting operating condition below which operation is prohibited. Surge control on compressors is usually achieved by opening a bypass valve on a line connecting the outlet to the inlet of the compressor. When the surge point is approached, the bypass valve is opened, and gas flows from the outlet to the inlet, thereby increasing the flow through the compressor and moving it away from the surge condition.
Positive-displacement compressors also exist and are used to compress low volumes to high pressures. Centrifugal compressors are used to compress higher volumes to moderate pressures and are often staged to obtain higher pressures. Figure 19.5 illustrates the inner workings of a compressor.
19.5.4.2 Compressor Staging
There are two limiting cases for compressor behavior: isothermal and isentropic. An actual compressor is neither isothermal nor isentropic; however, the behavior lies between these two limiting cases. From the general mechanical energy balance, compressor work is
where subscripts 1 and 2 denote compressor inlet and outlet, respectively. For the isothermal case, assuming ideal gas behavior (which will fail as the pressure increases but is sufficient to illustrate the basic concepts),
For isentropic compression, the relationship from thermodynamics for adiabatic, reversible, compression is
where γ = Cp/Cv, the ratio of the constant pressure and constant volume heat capacities. Using the compressor inlet as a reference point,
Solving Equation (19.76) for ρ, using that value in Equation (19.73), and integrating yields a well-known expression from thermodynamics for adiabatic, reversible, compression of an ideal gas:
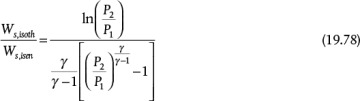
Taking the ratio of Equations (19.74) and (19.77), and realizing that T = T1 in Equation (19.74), since the temperature is constant at the inlet value in the isothermal case, yields
Figure 19.26 is a plot of Equation (19.78), with the dependent variable as the compression ratio, P2/P1. Figure 19.26 demonstrates that the reversible, adiabatic work for isothermal compression is always less than that for isentropic compression. As the compression ratio exceeds 3 to 4, the isothermal work is significantly less than the isentropic work, making isothermal compression desirable. Of course, since compressing a gas always increases the gas temperature, isothermal compression cannot be accomplished. However, isothermal compression can be approached by staging compressors with intercooling, as illustrated in Figure 19.27 for a two-stage configuration. Isothermal compression can be reached theoretically with an infinite number of compressors each with an infinitesimal temperature rise, hardly a practical situation. From thermodynamics, it can be shown that the minimum compressor work for staged adiabatic compressors, with interstage cooling to the feed temperature to the first compressor, is accomplished with an equal compression ratio in each compressor stage. This is not necessarily the economic optimum, which would require analysis of the capital cost of the compressor stages and heat exchangers, the operating cost of the compressor, and the utility cost of the cooling medium. However, the preceding analysis explains why compressors are usually staged when the compression ratio exceeds 3 to 4.
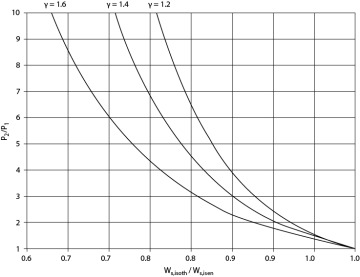
Figure 19.26 Comparison of Isothermal and Isentropic Work for Compressors

Figure 19.27 Example of Two−Stage Compressor Configuration
19.5.5 Performance of the Feed Section to a Process
A common feature of chemical processes is the mixing of reactant feeds before they enter a reactor. When two streams mix, they are at the same pressure. The consequences of this are illustrated by the following scenario.
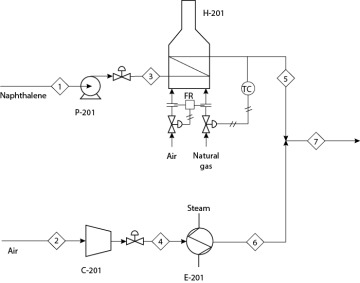
Phthalic anhydride can be produced by reacting naphthalene and oxygen. The feed section to a phthalic anhydride process is shown in Figure 19.28. The mixed feed enters a fluidized bed reactor operating at five times the minimum fluidization velocity. A stream table is given in Table 19.4. It is assumed that all frictional pressure losses are associated with equipment and that frictional losses in the piping are negligible. It is temporarily necessary to scale down production by 50%. The engineer must determine how to scale down the process and to determine the new flows and pressures.
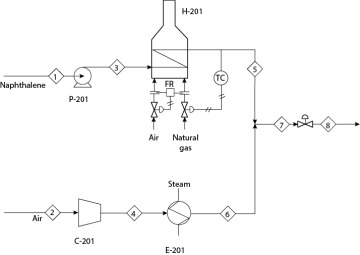
Figure 19.28 Feed Section to Phthalic Anhydride Process
Table 19.4 Partial Stream Table for Feed Section in Figure 19.27
Stream |
||||||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
P (kPa) |
80.00 |
101.33 |
343.0 |
268.0 |
243.0 |
243.0 |
243.0 |
200.0 |
Phase |
L |
V |
L |
V |
V |
V |
V |
V |
Naphthalene (Mg/h) |
12.82 |
— |
12.82 |
— |
12.82 |
— |
12.82 |
12.82 |
Air (Mg/h) |
— |
151.47 |
— |
151.47 |
— |
151.47 |
151.47 |
151.47 |
It is necessary to have pump and compressor curves in order to do the required calculations. In this example, equations for the pump curves are used. These equations can be obtained by fitting a polynomial to the curves provided by pump manufacturers. As discussed in Section 19.5.3, pump curves are usually expressed as pressure head versus volumetric flowrate so that they can be used for a liquid of any density. In this example, pressure head and volumetric flowrate have been converted to absolute pressure and mass flowrate using the density of the fluids involved. Pump P-201 operates at only one speed, and an equation for the pump curve is
Compressor C-201 operates at only one speed, and the equation for the compressor curve is
From Figure 19.27, it is seen that there is only one valve in the feed section, after the mixing point. Therefore, the only way to reduce the production of phthalic anhydride is to close the valve to the point at which the naphthalene feed is reduced by 50%. Example 19.21 illustrates the consequences of reducing the naphthalene feed rate by 50%.




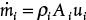 , canceling the ratio of densities for the same reason as above, and canceling the ratio of cross-sectional areas because the pipe has remained unchanged. Therefore, by assigning the base-case mass flow to have a value of 1, for a 25% scale-up, the new case has a mass flow of 1.25, and the ratio of pressure drops becomes
, canceling the ratio of densities for the same reason as above, and canceling the ratio of cross-sectional areas because the pipe has remained unchanged. Therefore, by assigning the base-case mass flow to have a value of 1, for a 25% scale-up, the new case has a mass flow of 1.25, and the ratio of pressure drops becomes
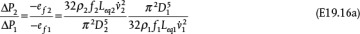



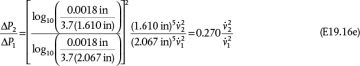



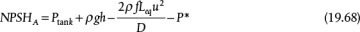
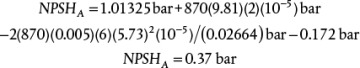
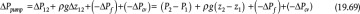

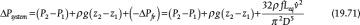
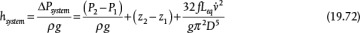



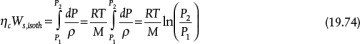


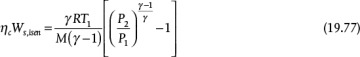
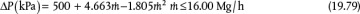
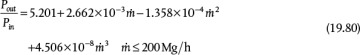
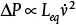 . Therefore, P5 = 510.73 kPa. Consequently, the pressure of Stream 6 must be 510.73 kPa. The flowrate of air can now be calculated from the compressor curve equation.
. Therefore, P5 = 510.73 kPa. Consequently, the pressure of Stream 6 must be 510.73 kPa. The flowrate of air can now be calculated from the compressor curve equation.