Process Fluid Mechanics
- 19.1 Basic Relationships in Fluid Mechanics
- 19.2 Fluid Flow Equipment
- 19.3 Frictional Pipe Flow
- 19.4 Other Flow Situations
- 19.5 Performance of Fluid Flow Equipment
- References
- Short Answer Questions
- Problems
This excerpt provides a more logical pedagogy for the design of basic process equipment including pipes, pumps, and compressors.
Save 35% off the list price* of the related book or multi-format eBook (EPUB + MOBI + PDF) with discount code ARTICLE.
* See informit.com/terms
The purpose of this chapter is to introduce the concepts needed to design piping systems, including pumps, compressors, turbines, valves, and other components, and to evaluate the performance of these systems once designed and implemented. The scope is limited to steady-state situations. Derivations are minimized, and the emphasis is on providing a set of useful, working equations that can be used to design and evaluate the performance of piping systems.
19.1 Basic Relationships in Fluid Mechanics
In expressing the basic relationships for fluid flow, a general control volume is used, as illustrated in Figure 19.1. This control volume can be the fluid inside the pipes and equipment connected by the pipes, with the possibility of multiple inputs and multiple outputs. For the simple case of one input and one output, the subscript 1 refers to the upstream side and the subscript 2 refers to the downstream side.
Figure 19.1 General Control Volume
19.1.1 Mass Balance
At steady state, mass is conserved, so the total mass flowrate (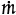 , mass/time) in must equal the total mass flowrate out. For a device with m inputs and n outputs, the appropriate relationship is given by Equation (19.1). For a single input and single output, Equation (19.2) is used.
, mass/time) in must equal the total mass flowrate out. For a device with m inputs and n outputs, the appropriate relationship is given by Equation (19.1). For a single input and single output, Equation (19.2) is used.
In describing fluid flow, it is necessary to write the mass flowrate in terms of both volumetric flowrate (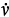 , volume/time) and velocity (u, length/time). These relationships are
, volume/time) and velocity (u, length/time). These relationships are
where ρ is the density (mass/volume) and A is the cross-sectional area for flow (length2). From Equation (19.3), for an incompressible fluid (constant density) at steady state, the volumetric flowrate is constant, and the velocity is constant for a constant cross-sectional area for flow. However, for a compressible fluid flowing with constant cross-sectional area, if the density changes, the volumetric flowrate and velocity both change in the opposite direction, since the mass flowrate is constant. Accordingly, if the density decreases, the volumetric flowrate and velocity both increase. For problems involving compressible flow, it is useful to define the superficial mass velocity, G (mass/area/time), as
The advantage of defining a superficial mass velocity is that it is constant for steady-state flow in a constant cross-sectional area, unlike density and velocity, and it shows that the product of density and velocity remains constant.
For a system with multiple inputs and/or multiple outputs at steady state, as is illustrated in Figure 19.2, the total mass flowrate into the system must equal the total mass flowrate out, Equation (19.1). However, the output mass flowrate in each section differs depending on the size, length, and elevation of the piping involved. These problems are discussed later.
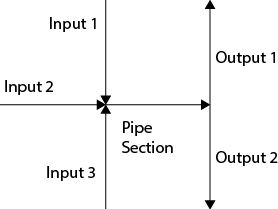
Figure 19.2 System with Multiple Inputs and Outputs
19.1.2 Mechanical Energy Balance
The mechanical energy balance represents the conversion between different forms of energy in piping systems. With the exception of temperature changes for a gas undergoing compression or expansion with no phase change, temperature is assumed to be constant. The mechanical energy balance is
In Equation (19.5) and throughout this chapter, the difference, Δ, represents the value at Point 2 minus the value at Point 1, that is, out − in. The units in Equation (19.5) are energy/mass or length2/time2. In SI units, since 1 J =1 kg m2/s2, it is clear that 1 J/kg = 1 m2/s2. In American Engineering units, since 1 lbf = 32.2 ft lbm/sec2, this conversion factor (often called gc) must be used to reconcile the units. The notation < > represents the appropriate average quantity.
The first term in Equation (19.5) is the enthalpy of the system. On the basis of the constant temperature assumption, only pressure is involved. For incompressible fluids, such as liquids, density is constant, and the term reduces to
For compressible fluids, the integral must be evaluated using an equation of state.
The second term in Equation (19.5) is the kinetic energy term. For turbulent flow, a reasonable assumption is that
For laminar flow,
For simplicity, < u2 > is hereafter represented as < u>2, which is shortened to u2.
The third term in Equation (19.5) is the potential energy term. Based on the general control volume, Δz is positive if Point 2 is at a higher elevation than Point 1.
The fourth term in Equation (19.5) is often called the energy “loss” due to friction. Of course, energy is not lost—it is just expended to overcome friction, and it manifests as a change in temperature. The procedures for calculating frictional losses are discussed later.
The last term in Equation (19.5) represents the shaft work, that is, the work done on the system (fluid) by a pump or compressor or the work done by the system on a turbine. These devices are not 100% efficient. For example, more work must be applied to the pump than is transferred to the fluid, and less work is generated by the turbine than is expended by the fluid. In this book, work is defined as positive if done on the system (pump, compressor) and negative if done by the fluid (turbine). This convention is consistent with the flow of energy in or out of the system; however, many textbooks use the reverse sign convention. Equipment such as pumps, compressors, and turbines are described in terms of their power, where power is the rate of doing work. Therefore, a device power (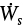 , energy/time) is defined as the product of the mass flowrate (mass/time) and the shaft work (energy/mass):
, energy/time) is defined as the product of the mass flowrate (mass/time) and the shaft work (energy/mass):
When efficiencies are included, the last term in Equation (19.5) becomes
19.1.3 Force Balance
The force balance is essentially a statement of Newton’s law. A common form for flow in pipes is
where F are the forces on the system. The underlined parameters indicate vectors, since there are three spatial components of a force balance. For steady-state flow and the typical forces involved in fluid flow, Equation (19.12) reduces to
where Fp is the pressure force on the system, Fd is the drag force on the system, Fg is the gravitational force on the system, and R is the restoring force on the system, that is, the force necessary to keep the system stationary. The term on the left side of Equation (19.12) is acceleration, confirming that Equation (19.12) is a statement of Newton’s law. The most common application of Equation (19.13) is to determine the restoring forces on an elbow. These problems are not discussed here.




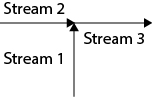
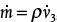 , so
, so 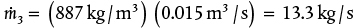 . Alternatively, the mass flowrate of Streams 1 and 2 could be calculated and added to get the same result.
. Alternatively, the mass flowrate of Streams 1 and 2 could be calculated and added to get the same result.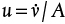 . Therefore,
. Therefore,
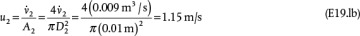


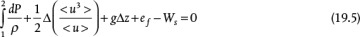




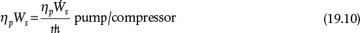

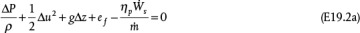
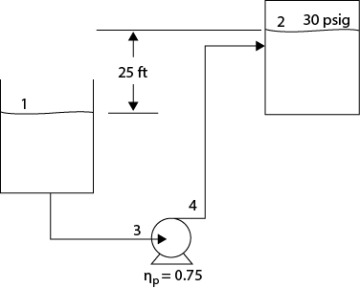

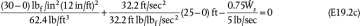
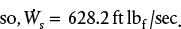


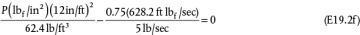
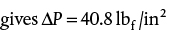 .
.



