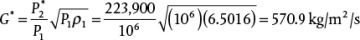19.3 Frictional Pipe Flow
19.3.1 Calculating Frictional Losses
The fourth term in Equation (19.5) must be evaluated to include friction in the mechanical energy balance. There are different expressions for this term depending on the type of flow and the system involved. In general, the friction term is
where L is the pipe length, D is the pipe diameter, and f is the Fanning friction factor. (The Fanning friction factor is typically used by chemical engineers. There is also the Moody friction factor, which is four times the Fanning friction factor. Care must be used when obtaining friction factor values from different sources. It is even more confusing, since the plot of friction factor versus Reynolds number is called a Moody plot for both friction factors.) The friction factor is a function of the Reynolds number (Re = Du ρ/μ, where μ is the fluid viscosity), and its form depends on the flow regime (laminar or turbulent), and for turbulent flow, f is also a function of the pipe roughness factor (e, a length that represents small asperities on the pipe wall; values are given at the top of Figure 19.6), which is a tabulated value. Historically, the friction factor was measured and the data were plotted in graphical form. Figure 19.6 is such a plot. A key observation from Figure 19.6 is that, with the exception of smooth pipes, the friction factor asymptotically approaches a constant value above a Reynolds number of approximately 105. This is called fully developed turbulent flow, and the friction factor becomes constant and can be used to simplify certain calculations, examples of which are presented later. Typical values for the pipe roughness for some common materials are shown at the top of Figure 19.6.
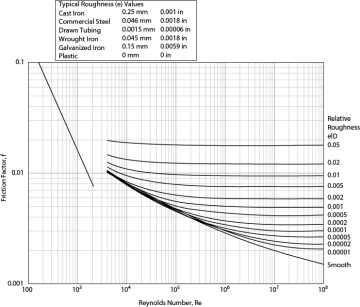
Figure 19.6 Moody Plot for the Fanning Friction Factor in Pipes
The friction factor for laminar flow is a theoretical result derivable from the Hagen-Poiseuille equation [6] and is valid for Re < 2100.
For turbulent flow, the data have been fit to equations. One such equation is the Pavlov equation ([7] [cited in Levenspiel [8]]):
The Pavlov equation provides results within a few percent of the measured data. There are more accurate equations; however, they are not explicit in the friction factor. Any of these curve fits provides significantly more accuracy than reading a graph.
For flow in pipes containing valves, elbows, and other pipe fittings, there are two common methods for including the additional frictional losses created by this equipment. One is the equivalent length method, whereby additional pipe length is added to the value of L in Equation (19.14). The other method is the velocity head method, in which a value (Ki) is assigned to each valve, fitting, and so on, and an additional frictional loss term is added to the frictional loss term in Equation (19.14). These terms are of the form
where the index i indicates a sum over all valves, elbows, and similar components in the system. If there are different pipe diameters within the system, the velocity in Equation (19.17) is specific to each section of pipe, and a term for each section of pipe must be included. It should be noted that the equivalent Ki value for straight pipe (Kpipe) is given by
Tables 19.2 and 19.3 show equivalent lengths and Ki values for some common items found in pipe networks, for turbulent flow and for laminar flow, respectively. The values are different for laminar and turbulent flow. Darby [9] presents analytical expressions for the K values that can be used for more exact calculations.
Table 19.2 Frictional Losses for Turbulent Flow
Type of Fitting or Valve |
Frictional Loss, Number of Velocity Heads, Kf |
Frictional Loss, Equivalent Length of Straight Pipe, in Pipe Diameters, L eq /D |
45° elbow |
0.35 |
17 |
90° elbow |
0.75 |
35 |
Tee |
1 |
50 |
Return bend |
1.5 |
75 |
Coupling |
0.04 |
2 |
Union |
0.04 |
2 |
Gate valve, wide open |
0.17 |
9 |
Gate valve, half open |
4.5 |
225 |
Globe valve, wide open |
6.0 |
300 |
Globe valve, half open |
9.5 |
475 |
Angle valve, wide open |
2.0 |
100 |
Check valve, ball |
70.0 |
3500 |
Check valve, swing |
2.0 |
100 |
Contraction |
0.55(1 – A2/A1) |
27.5(1 – A2/A1) |
Contraction A2 << A1 |
0.55 |
27.5 |
Expansion |
(1 – A1/A2)2 |
50(1 – A1/A2)2 |
Expansion A1 << A2 |
1 |
50 |
Source: From Geankoplis, C., Transport Processes and Separation Process Principles, 4th ed., (Upper Saddle River, NJ: Prentice Hall, 2003); Perry, R. H., and D. Green, Perry’s Chemical Engineers’ Handbook, 6th ed. (New York: McGraw-Hill, 1984), Section 5. |
||
Table 19.3 Frictional Loss for Laminar Flow
Frictional Loss, Number of Velocity Heads, Kf |
||||||
Reynolds number |
50 |
100 |
200 |
400 |
1000 |
Turbulent |
90° elbow |
17 |
7 |
2.5 |
1.2 |
0.85 |
0.75 |
Tee |
9 |
4.8 |
3.0 |
2.0 |
1.4 |
1.0 |
Globe valve |
28 |
22 |
17 |
14 |
10 |
6.0 |
Check valve, swing |
55 |
17 |
9 |
5.8 |
3.2 |
2.0 |
Source: From Geankoplis, C., Transport Processes and Separation Process Principles, 4th ed. (Upper Saddle River, NJ: Prentice Hall, 2003), 99–100, citing Kittredge, C. P., and D. S. Rowley, “Resistance Coefficients for Laminar and Turbulent Flow Through One-Half-Inch Valves and Fittings,” Trans. ASME, 79 (1957): 1759–1766. |
||||||
Another common situation involves frictional loss in a packed bed, that is, a vessel packed with solids. One application is if the solids are catalysts, making the packed bed a reactor. The frictional loss term for packed beds is obtained from the Ergun equation, which yields a friction term for a packed bed as
where us is the superficial velocity (based on pipe diameter, not particle diameter), Dp is the particle diameter (assumed spherical here; corrections are available for nonspherical shape), and ε is the packing void fraction, which is the volume fraction in the packed bed not occupied by solids. When Equation (19.19) is used in the mechanical energy balance, one unknown parameter, such as velocity, pressure drop, or particle diameter, can be obtained.
For incompressible flow in packed beds, the Ergun equation, Equation (19.19), is used for the friction term in the mechanical energy balance.
For the expansion and contraction losses, Ai is the cross-sectional area of the pipe, subscript 1 is the upstream area, and subscript 2 is the downstream area.
19.3.2 Incompressible Flow
19.3.2.1 Single-Pipe Systems
Incompressible flow problems fall into three categories:
Any parameter unknown in the mechanical energy balance other than velocity (flowrate) or diameter
Unknown velocity (flowrate)
Unknown diameter
For turbulent flow problems with any unknown other than velocity (or flowrate) or diameter, in the mechanical energy balance, Equation (19.5), there is a second unknown: the friction factor. The friction factor can be calculated from Equation (19.15). The solution method can use a sequential calculation, solving Equation (19.5) for the unknown once the friction factor is calculated. If there are valves, elbows, and so on, the length term in Equation (19.15) can be adjusted appropriately or Equation (19.17) can be used. Alternatively, Equations (19.14) and (19.16) can be solved simultaneously to yield all the unknowns. Example 19.5 shows both of these calculation methods. For laminar flow problems, Equation (19.15) can be combined with Equation (19.14) in the mechanical energy balance to solve any problem analytically.
For turbulent flow, if the velocity is unknown, Equations (19.5) and (19.15) must be solved simultaneously for the velocity or flowrate and the friction factor. When solving for a velocity directly, if the pump work term must be included, it is necessary to express the mass flowrate in terms of velocity. If solving for the volumetric flowrate, the second equality in Equation (19.13) must be used, and if a kinetic energy term is required in the mechanical energy balance, the velocities must be expressed in terms of volumetric flowrate. In the friction factor equation, the Reynolds number also needs to be expressed in terms of the volumetric flowrate as follows:
For laminar flow, an analytical solution is possible simply by using Equation (19.14) for the friction factor in the mechanical energy balance.
For turbulent flow, if the diameter is unknown, Equations (19.5) and (19.13) (second equality involving flowrate and diameter to the fifth power) must be solved simultaneously, using Equation (19.20) for the Reynolds number. For laminar flow, an analytical solution may once again be possible by using Equation (19.12) for the friction factor in the mechanical energy balance. If kinetic energy terms are involved, an unknown diameter will appear when expressing velocity in terms of flowrate. If minor losses are involved, the equivalent length will include a diameter term, and the K-value method will include a diameter in the conversion between flowrate and velocity.
Examples 19.4 and 19.5 illustrate the methods for solving these types of problems.
19.3.2.2 Multiple-Pipe Systems
For complex, multiple-pipe systems, including branching or mixing pipe systems, as illustrated in Figure 19.7, there are two sets of key relationships.
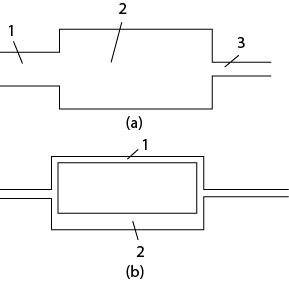
Figure 19.7 Multiple Pipe Systems: (a) Pipes of Different Diameters in Series, (b) Pipes of Different Diameters in Parallel
For pipes in series, the mass flowrate is constant and the pressure differences are additive:
For pipes in parallel, the mass flowrates are additive and the pressure differences are equal:
Equation (19.21) is just the mass balance; the mass flowrate through each section must be constant. Equation (19.22) just means that the pressure drops in all sections in series are additive.
In the case of parallel flow, Equation (19.23) means that the mass flowrates in and out of the parallel section are additive, since mass must be conserved. Equation (19.24) means that the pressure drops in parallel sections are equal. This is because mixing streams must be designed to be at the same pressure, or the flowrates will readjust so the pressures at the mixing point are identical. This concept is discussed in more detail later.
The solution method is to write all of the relevant equations, including the mechanical energy balance, friction factor expression, and mass balance, along with the appropriate constraints from Equations (19.21) through (19.24), and solve the equations simultaneously. It is understood that this method applies to any number of pipes in series or parallel.
When streams mix, the pressure will be the same. If a pipe system is designed such that the pressures at a mixing point are not the same, the flowrates will adjust (as illustrated in Example 19.9) to make the mixing-point pressures identical, and the flowrates will not be as designed. This is important because steady-state process simulators allow streams to be mixed at different pressures, and the lowest pressure is taken as the outlet pressure unless an outlet pressure or a mixing-point pressure drop is specified. Just because steady-state process simulators allow this to be done does not make it physically correct. Valves are used to reduce higher pressures to make the pressures equal at a mixing point. When using simulators, it is the user’s responsibility to include appropriate devices to make the simulation correspond to reality.
19.3.3 Compressible Flow
For compressible flow, the integral in the mechanical energy balance in Equation (19.5) must be evaluated, since the density is not constant. There are two limiting cases for frictional flow through a pipe section: isothermal flow and adiabatic flow. For isothermal flow of an ideal gas, the density is expressed as
where M is the molecular weight, and the integral can be evaluated. For adiabatic, reversible flow of an ideal gas, the temperature in Equation (19.25) is expressed in terms of pressure to evaluate the integral in Equation (19.5) using a relationship obtained from thermodynamics:
where
where Cp and Cv are the constant pressure and constant volume heat capacities, respectively. The results are expressed in terms of the superficial mass velocity, G. For isothermal, turbulent flow, the result, presented without derivation, is
which can be solved for an unknown pressure, superficial mass velocity (G), diameter (by expressing superficial mass velocity in terms of diameter), or length. For isothermal, laminar flow, the result is
Equation (19.29) is a quadratic in G, or if G is known, any other variable can be found. For adiabatic, turbulent flow, the result is
For compressible flow in packed beds, the Ergun equation, Equation (19.19), is used for the friction term, and the pressure term in the mechanical energy balance is integrated assuming either isothermal or adiabatic flow. For isothermal flow, the result is
where subscript 1 is upstream and subscript 2 is downstream. Quite often, it is stated that the mechanical energy balance for packed beds, which is the Ergun equation in Equation (19.19), can be used for gases as long as the pressure drop is less than 10% of the average pressure. However, with the computational tools now available, there is really no need for that approximation.
In Equations (19.28) through (19.33), it is assumed that the flow is in a pipe; therefore, there is no work term. The potential energy term is neglected because it is generally negligible for gases due to their low density.
19.3.4 Choked Flow
In evaluating the flow of compressible fluids, there exists a limit for the maximum velocity of the fluid (gas), that is, the speed of sound in the fluid. As an example, consider a pressurized gas in a supply tank (Tank 1) that is connected to a destination tank (Tank 2) via a pipe. Initially, Tank 1 and Tank 2 are at the same pressure, so no gas flows between them. Gradually, the pressure in Tank 2 is reduced and gas starts to flow from Tank 1 to Tank 2. It seems logical that the lower the pressure in Tank 2, the higher the gas flow rate is and the higher is the velocity of gas entering Tank 2. However, at some critical pressure for Tank 2, 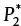 , the flow of gas into Tank 2, reaches sonic velocity (the speed of sound). Decreasing the tank pressure below this critical pressure has no effect on the exit velocity of the gas entering Tank 2; that is, it remains constant at the speed of sound. This phenomenon of choked flow occurs because the change in downstream pressure must propagate upstream for the change in flow to occur. The speed at which this propagation occurs is the speed of sound. Thus, when the gas velocity is at the speed of sound, any further decrease in downstream pressure cannot be propagated upstream, and the flow cannot increase further. Therefore, there is a critical (maximum) superficial mass velocity of gas, G*, that can be transferred from Tank 1 to Tank 2 through the pipe. The relationships for critical flow in pipes under turbulent flow conditions are as follows:
, the flow of gas into Tank 2, reaches sonic velocity (the speed of sound). Decreasing the tank pressure below this critical pressure has no effect on the exit velocity of the gas entering Tank 2; that is, it remains constant at the speed of sound. This phenomenon of choked flow occurs because the change in downstream pressure must propagate upstream for the change in flow to occur. The speed at which this propagation occurs is the speed of sound. Thus, when the gas velocity is at the speed of sound, any further decrease in downstream pressure cannot be propagated upstream, and the flow cannot increase further. Therefore, there is a critical (maximum) superficial mass velocity of gas, G*, that can be transferred from Tank 1 to Tank 2 through the pipe. The relationships for critical flow in pipes under turbulent flow conditions are as follows:
Isothermal flow:
and
Adiabatic flow:
and
When evaluating compressible flows, a check for critical flow conditions in the system should always be done. Usually, critical flow is not an issue when P2 > 0.5P1, but it is always a good idea to check. The use of Equations (19.32) through (19.35) is illustrated in Example 19.10.


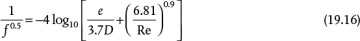


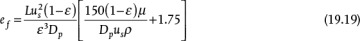
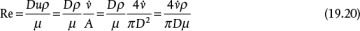
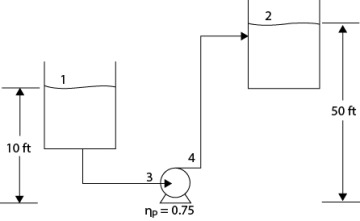

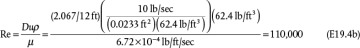
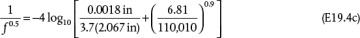

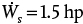 . If the contribution of each term is enumerated, 0.97 hp is to overcome the potential energy and 0.48 hp is to overcome the discharge line friction, with 0.056 hp to overcome the suction line friction. Generally, potential energy differences and pressure differences are more significant than frictional losses.
. If the contribution of each term is enumerated, 0.97 hp is to overcome the potential energy and 0.48 hp is to overcome the discharge line friction, with 0.056 hp to overcome the suction line friction. Generally, potential energy differences and pressure differences are more significant than frictional losses.

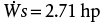 .
.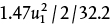 is added to the mechanical energy balance. For the discharge side, K = 2(0.75) + 0.17 + 9.5 + 1 = 12.17, so a term of
is added to the mechanical energy balance. For the discharge side, K = 2(0.75) + 0.17 + 9.5 + 1 = 12.17, so a term of 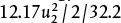 is added to the mechanical energy balance. The result is 2.12 hp, which illustrates that the two methods do not give exactly the same results. The difference is because both methods are empirical and are subject to uncertainties. Either method is within the typical tolerance of a design specification. To provide flexibility and since pumps are typically available at fixed values, at least a 3 hp pump would probably be used here, and valves would be used to adjust the flowrate to the desired value.
is added to the mechanical energy balance. The result is 2.12 hp, which illustrates that the two methods do not give exactly the same results. The difference is because both methods are empirical and are subject to uncertainties. Either method is within the typical tolerance of a design specification. To provide flexibility and since pumps are typically available at fixed values, at least a 3 hp pump would probably be used here, and valves would be used to adjust the flowrate to the desired value.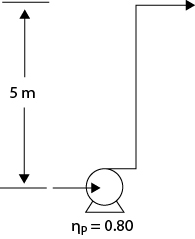



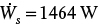 .
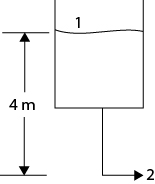
.
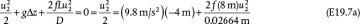
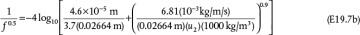
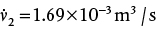 and
and 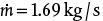 . Now, the Reynolds number must be checked using the calculated velocity, and Re = 80,960, so the turbulent flow assumption is valid.
. Now, the Reynolds number must be checked using the calculated velocity, and Re = 80,960, so the turbulent flow assumption is valid.

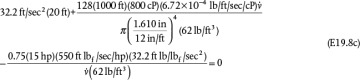
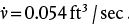 . Checking the Reynolds number,
. Checking the Reynolds number,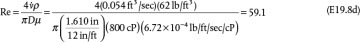







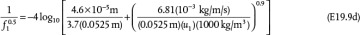
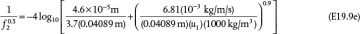
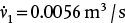 and
and 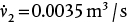 . While Branch 2 is shorter, the smaller diameter has a stronger effect on the friction, as seen by the fifth-power dependence in Equation (19.14), so Branch 2 has a smaller flowrate.
. While Branch 2 is shorter, the smaller diameter has a stronger effect on the friction, as seen by the fifth-power dependence in Equation (19.14), so Branch 2 has a smaller flowrate.



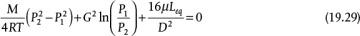
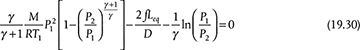
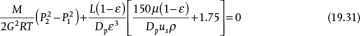



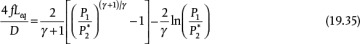
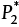 . An approximation can be made by assuming that the flow is fully developed turbulent and then checking this assumption. For fully developed turbulent flow, from Equation (19.16),
. An approximation can be made by assuming that the flow is fully developed turbulent and then checking this assumption. For fully developed turbulent flow, from Equation (19.16),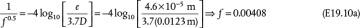
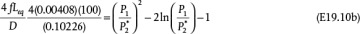
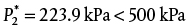 ; therefore, the flow is not choked. The actual friction factor is within a few percent of that calculated in Equation (E19.10a), and this difference does not affect the result regarding whether the flow is choked.
; therefore, the flow is not choked. The actual friction factor is within a few percent of that calculated in Equation (E19.10a), and this difference does not affect the result regarding whether the flow is choked.
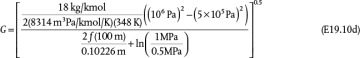
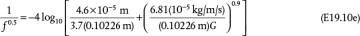
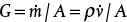 , using the exact solution, with the density calculated using the ideal gas law ρ = PM/RT,
, using the exact solution, with the density calculated using the ideal gas law ρ = PM/RT,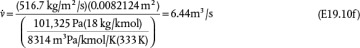
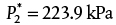 or less, then the superficial mass velocity would be at its maximum value, given by Equation (19.32) (where ρ1 = 6.5016 kg/m3):
or less, then the superficial mass velocity would be at its maximum value, given by Equation (19.32) (where ρ1 = 6.5016 kg/m3):