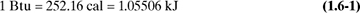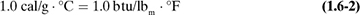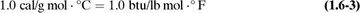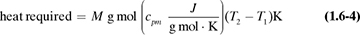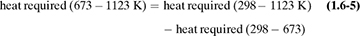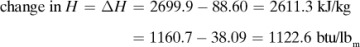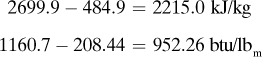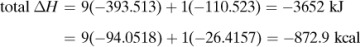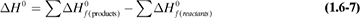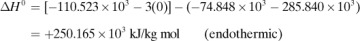Introduction to Engineering Principles and Units

Jun 12, 2018

📄 Contents

␡

⎙ Print

< Back Page 7 of 13 Next >

This chapter is from the book 

Transport Processes and Separation Process Principles, 5th Edition

Learn More Buy

1.6 Energy and Heat Units

1.6A Joule, Calorie, and Btu

In a manner similar to that used in making material balances on chemical and biological processes, we can also make energy balances on a process. Often, a large portion of the energy entering or leaving a system is in the form of heat. Before such energy or heat balances are made, we must understand the various types of energy and heat units.

In the SI system, energy is given in joules (J) or kilojoules (kJ). Energy is also expressed in btu (British thermal units) or cal (calories). The calorie (abbreviated as cal) is defined as the amount of heat needed to heat 1.0 g water 1.0°C (from 14.5°C to 15.5°C). Also, 1 kcal (kilocalorie) = 1000 cal. The btu is defined as the amount of heat needed to raise 1.0 lb water 1°F. Hence, from Appendix A.1,

Click to view larger image

1.6B Heat Capacity

The heat capacity of a substance is defined as the amount of heat necessary to increase the temperature by 1 degree. It can be expressed for 1 g, 1 lb, 1 g mol, 1 kg mol, or 1 lb mol of the substance. For example, a heat capacity is expressed in SI units as J/kg mol · K; in other units as cal/g · °C, cal/g mol · °C, kcal/kg mol · °C, Btu/lb_m · °F, or btu/lb mol · °F.

It can be shown that the actual numerical value of a heat capacity is the same in mass units or in molar units. That is,

Click to view larger image

Click to view larger image

For example, to prove this, suppose that a substance has a heat capacity of 0.8 btu/lb_m · °F. The conversion is made using 1.8°F for 1°C or 1 K, 252.16 cal for 1 btu, and 453.6 g for 1 lb_m, as follows:

Click to view larger image

The heat capacities of gases (also called specific heat) at constant pressure c_p are functions of temperature and, for engineering purposes, can often be assumed to be independent of pressure up to several atmospheres. In most process-engineering calculations, one is usually interested in the amount of heat needed to heat a gas from one temperature t₁ to another at t₂. Since the c_p varies with temperature, an integration must be performed or a suitable mean c_pm used. These mean values for gases have been obtained for T₁ of 298 K or 25°C (77°F) and various T₂ values, and are tabulated in Table 1.6-1 at 101.325 kPa pressure or less as c_pm in kJ/kg mol · K at various values of T₂ in K or °C.

Table 1.6-1. Mean Molar Heat Capacities of Gases Between 298 and TK (25 and T°C) at 101.325 kPa or Less (SI Units: c_p = kJ/kg mol · K)

T(K)	T(°C)	H₂	N₂	CO	Air	O₂	H₂O	CO₂	CH₄	SO₂
298	25	28.86	29.14	29.16	29.19	29.38	33.59	37.20	35.8	39.9
373	100	28.99	29.19	29.24	29.29	29.66	33.85	38.73	37.6	41.2
473	200	29.13	29.29	29.38	29.40	30.07	34.24	40.62	40.3	42.9
573	300	29.18	29.46	29.60	29.61	30.53	34.39	42.32	43.1	44.5
673	400	29.23	29.68	29.88	29.94	31.01	35.21	43.80	45.9	45.8
773	500	29.29	29.97	30.19	30.25	31.46	35.75	45.12	48.8	47.0
873	600	29.35	30.27	30.52	30.56	31.89	36.33	46.28	51.4	47.9
973	700	29.44	30.56	30.84	30.87	32.26	36.91	47.32	54.0	48.8
1073	800	29.56	30.85	31.16	31.18	32.62	37.53	48.27	56.4	49.6
1173	900	29.63	31.16	31.49	31.48	32.97	38.14	49.15	58.8	50.3
1273	1000	29.84	31.43	31.77	31.79	33.25	38.71	49.91	61.0	50.9
1473	1200	30.18	31.97	32.30	32.32	33.78	39.88	51.29	64.9	51.9
1673	1400	30.51	32.40	32.73	32.76	34.19	40.90	52.34

Mean Molar Heat Capacities of Gases Between 25 and T°C at 1 atm Pressure or Less (English Units: cp = btu/lb mol · °F)

T(°C)	H₂	N₂	CO	Air	O₂	NO	H₂O	CO₂	HCl	Cl₂	CH₄	SO₂	C₂H₄	SO₃	C₂H₆
25	6.894	6.961	6.965	6.972	7.017	7.134	8.024	8.884	6.96	8.12	8.55	9.54	10.45	12.11	12.63
100	6.924	6.972	6.983	6.996	7.083	7.144	8.084	9.251	6.97	8.24	8.98	9.85	11.35	12.84	13.76
200	6.957	6.996	7.017	7.021	7.181	7.224	8.177	9.701	6.98	8.37	9.62	10.25	12.53	13.74	15.27
300	6.970	7.036	7.070	7.073	7.293	7.252	8.215	10.108	7.00	8.48	10.29	10.62	13.65	14.54	16.72
400	6.982	7.089	7.136	7.152	7.406	7.301	8.409	10.462	7.02	8.55	10.97	10.94	14.67	15.22	18.11
500	6.995	7.159	7.210	7.225	7.515	7.389	8.539	10.776	7.06	8.61	11.65	11.22	15.60	15.82	19.39
600	7.011	7.229	7.289	7.299	7.616	7.470	8.678	11.053	7.10	8.66	12.27	11.45	16.45	16.33	20.58
700	7.032	7.298	7.365	7.374	7.706	7.549	8.816	11.303	7.15	8.70	12.90	11.66	17.22	16.77	21.68
800	7.060	7.369	7.443	7.447	7.792	7.630	8.963	11.53	7.21	8.73	13.48	11.84	17.95	17.17	22.72
900	7.076	7.443	7.521	7.520	7.874	7.708	9.109	11.74	7.27	8.77	14.04	12.01	18.63	17.52	23.69
1000	7.128	7.507	7.587	7.593	7.941	7.773	9.246	11.92	7.33	8.80	14.56	12.15	19.23	17.86	24.56
1100	7.169	7.574	7.653	7.660	8.009	7.839	9.389	12.10	7.39	8.82	15.04	12.28	19.81	18.17	25.40
1200	7.209	7.635	7.714	7.719	8.068	7.898	9.524	12.25	7.45	8.94	15.49	12.39	20.33	18.44	26.15
1300	7.252	7.692	7.772	7.778	8.123	7.952	9.66	12.39
1400	7.288	7.738	7.818	7.824	8.166	7.994	9.77	12.50
1500	7.326	7.786	7.866	7.873	8.203	8.039	9.89	12.69
1600	7.386	7.844	7.922	7.929	8.269	8.092	9.95	12.75
1700	7.421	7.879	7.958	7.965	8.305	8.124	10.13	12.70
1800	7.467	7.924	8.001	8.010	8.349	8.164	10.24	12.94
1900	7.505	7.957	8.033	8.043	8.383	8.192	10.34	13.01
2000	7.548	7.994	8.069	8.081	8.423	8.225	10.43	13.10
2100	7.588	8.028	8.101	8.115	8.460	8.255	10.52	13.17
2200	7.624	8.054	8.127	8.144	8.491	8.277	10.61	13.24

Source: O. A. Hougen, K. W. Watson, and R. A. Ragatz, Chemical Process Principles, Part I, 2nd ed. New York: John Wiley & Sons, Inc., 1954.

EXAMPLE 1.6-1. Heating of N₂ Gas

The gas N₂ at 1 atm pressure absolute is being heated in a heat exchanger. Calculate the amount of heat needed in J to heat 3.0 g mol N₂ in the following temperature ranges:

298–673 K (25–400°C)
298–1123 K (25–850°C)
673–1123 K (400–850°C)

Solution: For case (a), Table 1.6-1 gives c_pm values at 1 atm pressure or less, which can be used up to several atm pressures. For N₂ at 673 K, c_pm = 29.68 kJ/kg mol · K or 29.68 J/g mol · K. This is the mean heat capacity for the range 298–673 K:

Click to view larger image

Substituting the known values,

heat required = (3.0)(29.68)(673 – 298) = 33 390 J

For case (b), the c_pm at 1123 K (obtained by linear interpolation between 1073 and 1173 K) is 31.00 J/g mol · K:

heat required = (3.0)(31.00)(1123 – 298) = 76 725 J

For case (c), there is no mean heat capacity for the interval 673–1123 K. However, we can use the heat required to heat the gas from 298 to 673 K in case (a) and subtract it from case (b), which includes the heat required to go from 298 to 673 K plus 673 to 1123 K:

Click to view larger image

Substituting the proper values into Eq. (1.6-5),

heat required = 76 725 – 33 390 = 43 335 J

When heating a gas mixture, the total heat required is determined by first calculating the heat required for each individual component and then adding the results to obtain the total.

The heat capacities of solids and liquids are also functions of temperature and independent of pressure. Data are given in Appendix A.2, Physical Properties of Water; A.3, Physical Properties of Inorganic and Organic Compounds; and A.4, Physical Properties of Foods and Biological Materials. More data are available in (P1) in the References section at the end of this chapter.

The enthalpy, H, of a substance in J/kg represents the sum of the internal energy plus the pressure–volume term. For no reaction and a constant-pressure process with a change in temperature, the heat change as computed from Eq. (1.6-4) is the difference in enthalpy, ΔH, of the substance relative to a given temperature or base point. In other units, H = btu/lb_m or cal/g.

1.6C Latent Heat and Steam Tables

Whenever a substance undergoes a change of phase, relatively large amounts of heat change are involved at a constant temperature. For example, ice at 0°C and 1 atm pressure can absorb 6013.4 kJ/kg mol. This enthalpy change is called the latent heat of fusion. Data for other compounds are available in various handbooks (P1, W1).

When a liquid phase vaporizes to a vapor phase under its vapor pressure at constant temperature, an amount of heat called the latent heat of vaporization must be added. For water at 25°C and a pressure of 23.75 mmHg, the latent heat is 44 020 kJ/kg mol, and at 25°C and 760 mmHg, 44 045 kJ/kg mol. Hence, the effect of pressure can be neglected in these types of engineering calculations. However, there is a large effect of temperature on the latent heat of water. Also, the effect of pressure on the heat capacity of liquid water is small and can be neglected.

Since water is a very common chemical, the thermodynamic properties of it have been compiled in steam tables and are given in Appendix A.2 in SI and in English units.

EXAMPLE 1.6-3. Use of Steam Tables

Find the enthalpy change (i.e., how much heat must be added) for each of the following cases using SI and English units:

Heating 1 kg (lb_m) water from 21.11°C (70°F) to 60°C (140°F) at 101.325 kPa (1 atm) pressure
Heating 1 kg (lb_m) water from 21.11°C (70°F) to 115.6°C (240°F) and vaporizing at 172.2 kPa (24.97 psia)
Vaporizing 1 kg (lb_m) water at 115.6°C (240°F) and 172.2 kPa (24.97 psia)

Solution: For part (a), the effect of pressure on the enthalpy of liquid water is negligible. From Appendix A.2,

Click to view larger image

In part (b), the enthalpy at 115.6°C (240°F) and 172.2 kPa (24.97 psia) of the saturated vapor is 2699.9 kJ/kg or 1160.7 btu/lb_m.

Click to view larger image

The latent heat of water at 115.6°C (240°F) in part (c) is

1.6D Heat of Reaction

When chemical reactions occur, heat effects always accompany these reactions. This area where energy changes occur is often called thermochemistry. For example, when HCl is neutralized with NaOH, heat is given off and the reaction is exothermic. Heat is absorbed in an endothermic reaction. This heat of reaction is dependent on the chemical nature of each reacting material and product, and on their physical states.

For purposes of organizing data, we define a standard heat of reaction ΔH⁰ as the change in enthalpy when 1 kg mol reacts under a pressure of 101.325 kPa at a temperature of 298 K (25°C). For example, for the reaction

Click to view larger image

the ΔH⁰ is –285.840 × 10³ kJ/kg mol or –68.317 kcal/g mol. The reaction is exothermic and the value is negative since the reaction loses enthalpy. In this case, the H₂ gas reacts with the O₂ gas to give liquid water, all at 298 K (25°C).

Special names are given to ΔH⁰ depending upon the type of reaction. When the product is formed from the elements, as in Eq. (1.6-6), we call ΔH⁰ the heat of formation of the product water, 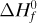. For the combustion of CH₄ to form CO₂ and H₂O, we call it heat of combustion, 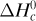. Data are given in Appendix A.3 for various values of .

EXAMPLE 1.6-4. Combustion of Carbon

A total of 10.0 g mol of carbon graphite is burned in a calorimeter held at 298 K and 1 atm. The combustion is incomplete and 90% of the C goes to CO₂ and 10% to CO. What is the total enthalpy change in kJ and kcal?

Solution: From Appendix A.3, the for carbon going to CO₂ is –393.513 × 10³ kJ/kg mol or –94.0518 kcal/g mol, and for carbon going to CO it is –110.523 × 10³ kJ/kg mol or –26.4157 kcal/g mol. Since 9 mol CO₂ and 1 mol CO are formed,

Click to view larger image

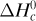If a table of heats of formation, 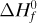, of compounds is available, the standard heat of the reaction, ΔH⁰, can be calculated by

Click to view larger image

In Appendix A.3, a short table of some values of ΔH_f is given. Other data are also available (H1, P1, S1).

EXAMPLE 1.6-5. Reaction of Methane

For the following reaction of 1 kg mol of CH₄ at 101.32 kPa and 298 K,

CH₄(g) + H₂O(l) → CO(g) + 3H₂(g)

calculate the standard heat of reaction ΔH⁰ at 298 K in kJ.

Solution: From Appendix A.3, the following standard heats of formation are obtained at 298 K:

	(kJ/kg mol)
CH₄(g)	–74.848 × 10³
H₂O(l)	–285.840 × 10³
CO(g)	–110.523 × 10³
H₂(g)	0

Note that the of all elements is, by definition, zero. Substituting into Eq. (1.6-7),

Click to view larger image

< Back Page 7 of 13 Next >

🔖 Save To Your Account

InformIT Promotional Mailings & Special Offers

I would like to receive exclusive offers and hear about products from InformIT and its family of brands. I can unsubscribe at any time.

Privacy Notice

Overview

Pearson Education, Inc., 221 River Street, Hoboken, New Jersey 07030, (Pearson) presents this site to provide information about products and services that can be purchased through this site.

This privacy notice provides an overview of our commitment to privacy and describes how we collect, protect, use and share personal information collected through this site. Please note that other Pearson websites and online products and services have their own separate privacy policies.

Collection and Use of Information

To conduct business and deliver products and services, Pearson collects and uses personal information in several ways in connection with this site, including:

Questions and Inquiries

For inquiries and questions, we collect the inquiry or question, together with name, contact details (email address, phone number and mailing address) and any other additional information voluntarily submitted to us through a Contact Us form or an email. We use this information to address the inquiry and respond to the question.

Online Store

For orders and purchases placed through our online store on this site, we collect order details, name, institution name and address (if applicable), email address, phone number, shipping and billing addresses, credit/debit card information, shipping options and any instructions. We use this information to complete transactions, fulfill orders, communicate with individuals placing orders or visiting the online store, and for related purposes.

Surveys

Pearson may offer opportunities to provide feedback or participate in surveys, including surveys evaluating Pearson products, services or sites. Participation is voluntary. Pearson collects information requested in the survey questions and uses the information to evaluate, support, maintain and improve products, services or sites, develop new products and services, conduct educational research and for other purposes specified in the survey.

Contests and Drawings

Occasionally, we may sponsor a contest or drawing. Participation is optional. Pearson collects name, contact information and other information specified on the entry form for the contest or drawing to conduct the contest or drawing. Pearson may collect additional personal information from the winners of a contest or drawing in order to award the prize and for tax reporting purposes, as required by law.

Newsletters

If you have elected to receive email newsletters or promotional mailings and special offers but want to unsubscribe, simply email information@informit.com.

Service Announcements

On rare occasions it is necessary to send out a strictly service related announcement. For instance, if our service is temporarily suspended for maintenance we might send users an email. Generally, users may not opt-out of these communications, though they can deactivate their account information. However, these communications are not promotional in nature.

Customer Service

We communicate with users on a regular basis to provide requested services and in regard to issues relating to their account we reply via email or phone in accordance with the users' wishes when a user submits their information through our Contact Us form.

Other Collection and Use of Information

Application and System Logs

Pearson automatically collects log data to help ensure the delivery, availability and security of this site. Log data may include technical information about how a user or visitor connected to this site, such as browser type, type of computer/device, operating system, internet service provider and IP address. We use this information for support purposes and to monitor the health of the site, identify problems, improve service, detect unauthorized access and fraudulent activity, prevent and respond to security incidents and appropriately scale computing resources.

Web Analytics

Pearson may use third party web trend analytical services, including Google Analytics, to collect visitor information, such as IP addresses, browser types, referring pages, pages visited and time spent on a particular site. While these analytical services collect and report information on an anonymous basis, they may use cookies to gather web trend information. The information gathered may enable Pearson (but not the third party web trend services) to link information with application and system log data. Pearson uses this information for system administration and to identify problems, improve service, detect unauthorized access and fraudulent activity, prevent and respond to security incidents, appropriately scale computing resources and otherwise support and deliver this site and its services.

Cookies and Related Technologies

This site uses cookies and similar technologies to personalize content, measure traffic patterns, control security, track use and access of information on this site, and provide interest-based messages and advertising. Users can manage and block the use of cookies through their browser. Disabling or blocking certain cookies may limit the functionality of this site.

Do Not Track

This site currently does not respond to Do Not Track signals.

Security

Pearson uses appropriate physical, administrative and technical security measures to protect personal information from unauthorized access, use and disclosure.

Children

This site is not directed to children under the age of 13.

Marketing

Pearson may send or direct marketing communications to users, provided that

Pearson will not use personal information collected or processed as a K-12 school service provider for the purpose of directed or targeted advertising.
Such marketing is consistent with applicable law and Pearson's legal obligations.
Pearson will not knowingly direct or send marketing communications to an individual who has expressed a preference not to receive marketing.
Where required by applicable law, express or implied consent to marketing exists and has not been withdrawn.

Pearson may provide personal information to a third party service provider on a restricted basis to provide marketing solely on behalf of Pearson or an affiliate or customer for whom Pearson is a service provider. Marketing preferences may be changed at any time.

Correcting/Updating Personal Information

If a user's personally identifiable information changes (such as your postal address or email address), we provide a way to correct or update that user's personal data provided to us. This can be done on the Account page. If a user no longer desires our service and desires to delete his or her account, please contact us at customer-service@informit.com and we will process the deletion of a user's account.

Choice/Opt-out

Users can always make an informed choice as to whether they should proceed with certain services offered by InformIT. If you choose to remove yourself from our mailing list(s) simply visit the following page and uncheck any communication you no longer want to receive: www.informit.com/u.aspx.

Sale of Personal Information

Pearson does not rent or sell personal information in exchange for any payment of money.

While Pearson does not sell personal information, as defined in Nevada law, Nevada residents may email a request for no sale of their personal information to NevadaDesignatedRequest@pearson.com.

Supplemental Privacy Statement for California Residents

California residents should read our Supplemental privacy statement for California residents in conjunction with this Privacy Notice. The Supplemental privacy statement for California residents explains Pearson's commitment to comply with California law and applies to personal information of California residents collected in connection with this site and the Services.

Sharing and Disclosure

Pearson may disclose personal information, as follows:

As required by law.
With the consent of the individual (or their parent, if the individual is a minor)
In response to a subpoena, court order or legal process, to the extent permitted or required by law
To protect the security and safety of individuals, data, assets and systems, consistent with applicable law
In connection the sale, joint venture or other transfer of some or all of its company or assets, subject to the provisions of this Privacy Notice
To investigate or address actual or suspected fraud or other illegal activities
To exercise its legal rights, including enforcement of the Terms of Use for this site or another contract
To affiliated Pearson companies and other companies and organizations who perform work for Pearson and are obligated to protect the privacy of personal information consistent with this Privacy Notice
To a school, organization, company or government agency, where Pearson collects or processes the personal information in a school setting or on behalf of such organization, company or government agency.

Links

This web site contains links to other sites. Please be aware that we are not responsible for the privacy practices of such other sites. We encourage our users to be aware when they leave our site and to read the privacy statements of each and every web site that collects Personal Information. This privacy statement applies solely to information collected by this web site.

Requests and Contact

Please contact us about this Privacy Notice or if you have any requests or questions relating to the privacy of your personal information.

Changes to this Privacy Notice

We may revise this Privacy Notice through an updated posting. We will identify the effective date of the revision in the posting. Often, updates are made to provide greater clarity or to comply with changes in regulatory requirements. If the updates involve material changes to the collection, protection, use or disclosure of Personal Information, Pearson will provide notice of the change through a conspicuous notice on this site or other appropriate way. Continued use of the site after the effective date of a posted revision evidences acceptance. Please contact us if you have questions or concerns about the Privacy Notice or any objection to any revisions.

Last Update: November 17, 2020

Email Address

Introduction to Engineering Principles and Units

This chapter is from the book

This chapter is from the book

This chapter is from the book 

1.6 Energy and Heat Units

1.6A Joule, Calorie, and Btu

1.6B Heat Capacity

Table 1.6-1. Mean Molar Heat Capacities of Gases Between 298 and TK (25 and T°C) at 101.325 kPa or Less (SI Units: cp = kJ/kg mol · K)

Mean Molar Heat Capacities of Gases Between 25 and T°C at 1 atm Pressure or Less (English Units: cp = btu/lb mol · °F)

1.6C Latent Heat and Steam Tables

1.6D Heat of Reaction

InformIT Promotional Mailings & Special Offers

Overview

Collection and Use of Information

Questions and Inquiries

Online Store

Surveys

Contests and Drawings

Newsletters

Service Announcements

Customer Service

Other Collection and Use of Information

Application and System Logs

Web Analytics

Cookies and Related Technologies

Do Not Track

Security

Children

Marketing

Correcting/Updating Personal Information

Choice/Opt-out

Sale of Personal Information

Supplemental Privacy Statement for California Residents

Sharing and Disclosure

Links

Requests and Contact

Changes to this Privacy Notice

Table 1.6-1. Mean Molar Heat Capacities of Gases Between 298 and TK (25 and T°C) at 101.325 kPa or Less (SI Units: c_p = kJ/kg mol · K)