- Random Numbers and Probability Distributions
- Casino Royale: Roll the Dice
- Normal Distribution
- The Student Who Taught Everyone Else
- Statistical Distributions in Action
- Hypothetically Yours
- The Mean and Kind Differences
- Worked-Out Examples of Hypothesis Testing
- Exercises for Comparison of Means
- Regression for Hypothesis Testing
- Analysis of Variance
- Significantly Correlated
- Summary
This chapter is from the book
This chapter is from the book
This chapter is from the book
Regression for Hypothesis Testing
So far, I have relied on the traditional tools for hypothesis testing that are prescribed in texts for statistical analysis and data science. I would argue that regression analysis, which I explain in detail in Chapter 7, “Why Tall Parents Don’t Have Even Taller Children,” could also be used to compare means of two or more groups. I favor regression analysis over other techniques primarily because of the simplicity in its application, which is a desired feature for most data scientists.
Let us focus on the teaching ratings example where we determine whether the average teaching evaluation differed for males and females. I have noted earlier that the average teaching evaluation for female instructors was 3.90 and for males 4.07.
Assuming equal variances, I conducted a t-test and concluded that a statistically significant difference in teaching evaluations existed for males and females (see Figure 6.35).
)
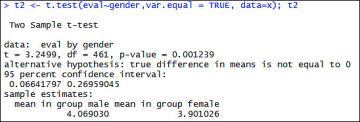
Figure 6.35 Equal variances two-tailed t-test to determine gender-based differences in teaching evaluations
The p-value of 0.0012 suggests that I can reject the null hypothesis of equal means and conclude that the average teaching evaluations between male and female instructors differ. Now let us attempt the same problem using a regression model. Figure 6.36 presents the output from the regression model.
)
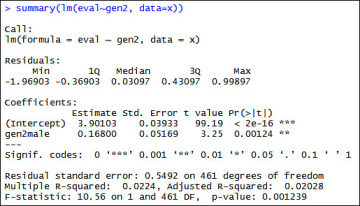
Figure 6.36 Regression model output for gender differences in teaching evaluations
Note that the column tvalue under Coefficients reports 3.25 for the row labelled as gen2male. This statistic is identical to the t-value obtained in the traditional t-test assuming equal variances. Furthermore, the column labelled Pr(>|t|) reports 0.00124 as the p-value for gen2male, which is again identical to the p-value reported in the t-test. Thus, we can see that when we assume equal variances, a regression model generates identical results.
The real benefit of the regression model emerges when we compare the means for more than two groups. t-tests are restricted to comparison of two groups. Regression models are useful when the null hypothesis states that the average values are the same for multiple groups.
To illustrate this point, I have categorized the age variable into a factor variable with three categories namely young, mid-age, and old. I would like to know whether a statistically significant difference exists between the teaching evaluation scores for young, mid-age, and old instructors. Again, I estimate a simple regression model (see Figure 6.37) to test the hypothesis. Figure 6.37 shows the results, and the R code follows.
x$f.age <- cut(x$age, breaks = 3)
x$f.age <- factor(x$f.age,labels=c("young", "mid age", "old"))
cbind(mean.eval=tapply(x$eval,x$f.age,mean),observations=table(x$f.age))
plot(x$age,x$eval,pch=20)
summary(lm(eval~f.age, data=x))
)
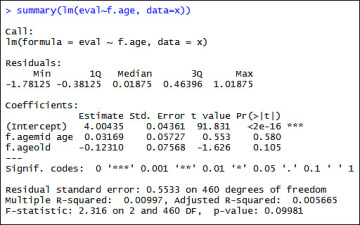
Figure 6.37 Regression model output for teaching evaluations based on age differences
I see that the values reported under the column labelled Pr(>|t|) in Figure 6.37 for the two categories of age; namely f.age mid age and f.age old are greater than .05. I therefore fail to reject the null hypothesis and conclude that average teaching evaluations do not differ by age in our sample.
Note that mid-age and old-age are represented in the model, whereas the category young is missing from the model. In regression models, when factor variables are used as explanatory variables, one arbitrarily chosen category, in this case young, is omitted from the output, and is used as the base against which other categories are compared.
The purpose here is not to explain the intricacies of regression models. Instead, my intent is to indicate a possible use of regression models for hypothesis testing. I do, however, explain the workings of regression models in Chapter 7.