- Random Numbers and Probability Distributions
- Casino Royale: Roll the Dice
- Normal Distribution
- The Student Who Taught Everyone Else
- Statistical Distributions in Action
- Hypothetically Yours
- The Mean and Kind Differences
- Worked-Out Examples of Hypothesis Testing
- Exercises for Comparison of Means
- Regression for Hypothesis Testing
- Analysis of Variance
- Significantly Correlated
- Summary
The Great Recession in 2008 wiped clean the savings portfolios of hundreds of millions in North America and Europe. Before the recession, people like columnist Margaret Wente, who were fast approaching retirement, had a 10-year plan. But then a “black swan pooped all over it.”1
Nassim Nicholas Taleb, a New York-based professor of finance and a former finance practitioner, used the black swan analogy in his book of the same title to explain how past events are limited in forecasting the future.2 He mentions the surprise of the European settlers when they first arrived in Western Australia and spotted a black swan. Until then, Europeans believed all swans to be white. However, a single sighting of a black swan changed that conclusion forever. This is why Professor Taleb uses the black swan metaphor to highlight the importance of extremely rare events, which the data about the past might not be able to forecast. The same phenomenon is referred to as the “fat tails” of probability distributions that explain the odds of the occurrence of rare events.
The fat tails of probability distributions resulted in trillions of dollars of financial losses during the 2007–08 financial crisis. In a world where almost nothing looks and feels normal, the empirical analysis is rooted in a statistical model commonly referred as the Normal distribution. Because of the ease it affords, the Normal distribution and its variants serve as the backbone of statistical analysis in engineering, economics, finance, medicine, and social sciences. Most readers of this book are likely to be familiar with the bell-shaped symmetrical curve that stars in every text on statistics and econometrics.
Simply stated, the Normal distribution assigns a probability to a particular outcome from a range of possible outcomes. For instance, when meteorologists advise of a 30% chance of rainfall, they are relying on a statistical model to forecast the likelihood of rain based on past data. Such models are usually good in forecasting the likelihood of events that have occurred more frequently in the past. For instance, the models usually perform well in forecasting the likelihood of a small change in a stock market’s value. However, the models fail miserably in forecasting large swings in the stock market value. The rarer an event, the poorer will be the model’s ability to forecast its likelihood to occur. This phenomenon is referred to as the fat tail where the model assigns a very low, sometimes infinitely low, possibility of an event to occur. However, in the real world, such extreme events occur more frequently.
In Financial Risk Forecasting, Professor Jon Danielsson illustrates fat tails using the Great Recession as an example.3 He focuses on the S&P 500 index returns, which are often assumed to follow Normal distribution. He illustrates that during 1929 and 2009, the biggest one-day drop in S&P 500 returns was 23% in 1987. If returns were indeed Normally distributed, the probability of such an extreme crash would be 2.23 × 10–97 Professor Danielsson explains that the model predicts such an extreme crash to occur only once in 1095 years. Here lies the problem. The earth is believed to be roughly 107 years old and the universe is believed to be 1013 years old. Professor Danielsson explains that if we were to believe in Normal distribution, the 1987 single day-crash of 23% would happen in “once out of every 12 universes.”
The reality is that the extreme fluctuations in stock markets occur much more frequently than what the models based on Normal distribution suggest. Still, it continues to serve as the backbone of empirical work in finance and other disciplines.
With these caveats, I introduce the concepts discussed in this chapter. Most empirical research is concerned with comparisons of outcomes for different circumstances or groups. For instance, we are interested in determining whether male instructors receive higher teaching evaluations than female instructors. Such analysis falls under the umbrella of hypothesis testing, which happens to be the focus of this chapter.
I begin by introducing the very basic concepts of random numbers and probability distributions. I use the example of rolling two dice to introduce the fundamental concepts of probability distribution functions. I then proceed to a formal introduction of Normal and t-distributions, which are commonly used for statistical models. Finally, I explore hypothesis testing for the comparison of means and correlations.
I use data for high-performing basketball players to compare their career performances using statistical models. I also use the teaching evaluations data, which I have introduced in earlier chapters, to compare means for two or more groups.
Random Numbers and Probability Distributions
Hypothesis testing has a lot to do with probability distributions. Two such distributions, known as the normal or Gaussian distribution and the t-distribution, are frequently used. I restrict the discussion about probability distributions to these frequently used distributions.
Probability is a measure between zero and one of the likelihood that an event might occur. An event could be the likelihood of a stock market falling below or rising above a certain threshold. You are familiar with the weather forecast that often describes the likelihood of rainfall in terms of probability or chance. Thus, you often hear the meteorologists explain that the likelihood of rainfall is, for instance, 45%. Thus, 0.45 is the probability that the event, rainfall, might occur.
The subjective definitions of probability might be expressed as the probability of one’s favorite team winning the World Series or the probability that a particular stock market will fall by 10% in a given time period. Probability is also described as outcomes of experiments. For instance, if one were to flip a fair coin, the outcome of head or tail can be explained in probabilities. Similarly, the quality control division of a manufacturing firm often defines the probability of a defective product as the number of defective units produced for a certain predetermined production level.
I explain here some basic rules about probability calculations. The probability associated with any outcome or event must fall in the zero and one (0–1) interval. The probability of all possible outcomes must equate to one.
Tied with probability is the concept of randomness. A random variable is a numerical description of the outcome of an experiment. Random variables could be discrete or continuous. Discrete random variables assume a finite or infinite countable number of outcomes. For instance, the imperfections on a car that passes through the assembly line or the number of incorrectly filled orders at a grocery store are examples of random variables.
A continuous random variable could assume any real value possible within some limited range. For instance, if a factory produces and ships cereal in boxes, the average weight of a cereal box will be a continuous random variable. In finance, the daily return of a stock is a continuous variable.
Let us build on the definition of probability and random variables to describe probability distributions. A probability distribution is essentially a theoretical model depicting the possible values a random variable may assume along with the probability of occurrence. We can define probability distributions for both discrete and continuous random variables.
Consider the stock for Apple computers for the period covering January 2011 and December 2013. During this time, the average daily returns equaled 0.000706 with a standard deviation of 0.01774. I have plotted a histogram of daily return for the Apple stock and I have overlaid a normal distribution curve on top of the histogram shown in Figure 6.1. The bars in the histogram depict the actual distribution of the data and the theoretical probability distribution is depicted by the curve. I can see from the figure that the daily returns equaled zero or close to zero more frequently than depicted by the Normal distribution. Also, note that some negative daily returns were unusually large in magnitude, which are reflected by the values to the very left of the histogram beyond –0.05. I can conclude that while the Normal distribution curve assigns very low probability to very large negative values, the actual data set suggests that despite the low theoretical probability, such values have realized more frequently.
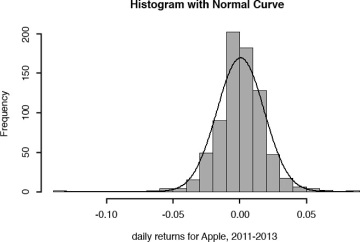
Figure 6.1 Histogram of daily Apple returns with a normal curve
