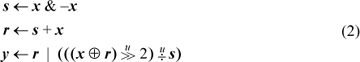Hacker's Delight: The Basics
- 2-1 Manipulating Rightmost Bits
- 2-2 Addition Combined with Logical Operations
- 2-3 Inequalities among Logical and Arithmetic Expressions
- 2-4 Absolute Value Function
- 2-5 Average of Two Integers
- 2-6 Sign Extension
- 2-7 Shift Right Signed from Unsigned
- 2-8 Sign Function
- 2-9 Three-Valued Compare Function
- 2-10 Transfer of Sign Function
- 2-11 Decoding a "Zero Means 2 **n" Field
- 2-12 Comparison Predicates
- 2-13 Overflow Detection
- 2-14 Condition Code Result of Add, Subtract, and Multiply
- 2-15 Rotate Shifts
- 2-16 Double-Length Add/Subtract
- 2-17 Double-Length Shifts
- 2-18 Multibyte Add, Subtract, Absolute Value
- 2-19 Doz, Max, Min
- 2-20 Exchanging Registers
- 2-21 Alternating among Two or More Values
- 2-22 A Boolean Decomposition Formula
- 2-23 Implementing Instructions for All 16 Binary Boolean Operations
2–1 Manipulating Rightmost Bits
Some of the formulas in this section find application in later chapters.
Use the following formula to turn off the rightmost 1-bit in a word, producing 0 if none (e.g., 01011000 ⇒ 01010000):
x & (x – 1)
This can be used to determine if an unsigned integer is a power of 2 or is 0: apply the formula followed by a 0-test on the result.
Use the following formula to turn on the rightmost 0-bit in a word, producing all 1’s if none (e.g., 10100111 ⇒ 10101111):
x | (x+ 1)
Use the following formula to turn off the trailing 1’s in a word, producing x if none (e.g., 10100111 ⇒ 10100000):
x & (x + 1)
This can be used to determine if an unsigned integer is of the form 2n– 1, 0, or all 1’s: apply the formula followed by a 0-test on the result.
Use the following formula to turn on the trailing 0’s in a word, producing x if none (e.g., 10101000 ⇒ 10101111):
x | (x– 1)
Use the following formula to create a word with a single 1-bit at the position of the rightmost 0-bit in x, producing 0 if none (e.g., 10100111 ⇒ 00001000):
¬x & (x + 1)
Use the following formula to create a word with a single 0-bit at the position of the rightmost 1-bit in x, producing all 1’s if none (e.g., 10101000 ⇒ 1111 0111):
¬x | (x – 1)
Use one of the following formulas to create a word with 1’s at the positions of the trailing 0’s in x, and 0’s elsewhere, producing 0 if none (e.g., 01011000 ⇒ 00000111):
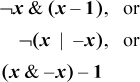
The first formula has some instruction-level parallelism.
Use the following formula to create a word with 0’s at the positions of the trailing 1’s in x, and 0’s elsewhere, producing all 1’s if none (e.g., 10100111 ⇒ 11111000):
¬x | (x + 1)
Use the following formula to isolate the rightmost 1-bit, producing 0 if none (e.g., 01011000 ⇒ 00001000):
x & (−x)
Use the following formula to create a word with 1’s at the positions of the rightmost 1-bit and the trailing 0’s in x, producing all 1’s if no 1-bit, and the integer 1 if no trailing 0’s (e.g., 01011000 ⇒ 00001111):
x ⊕ (x−1)
Use the following formula to create a word with 1’s at the positions of the rightmost 0-bit and the trailing 1’s in x, producing all 1’s if no 0-bit, and the integer 1 if no trailing 1’s (e.g., 01010111 ⇒ 00001111):
x ⊕ (x + 1)
Use either of the following formulas to turn off the rightmost contiguous string of 1’s (e.g., 01011100 ==> 01000000) [Wood]:
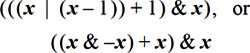
These can be used to determine if a nonnegative integer is of the form 2j − 2k for some j ≥ k≥ 0: apply the formula followed by a 0-test on the result.
De Morgan’s Laws Extended
The logical identities known as De Morgan’s laws can be thought of as distributing, or “multiplying in,” the not sign. This idea can be extended to apply to the expressions of this section, and a few more, as shown here. (The first two are De Morgan’s laws.)
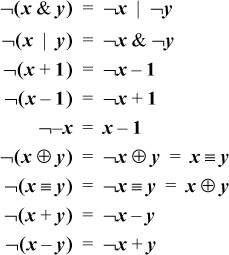
As an example of the application of these formulas, ¬(x | –(x + 1)) = ¬x &¬–(x + 1) = ¬x & ((x + 1) – 1) = ¬x & x = 0.
Right-to-Left Computability Test
There is a simple test to determine whether or not a given function can be implemented with a sequence of add’s, subtract’s, and’s, or’s, and not’s [War]. We can, of course, expand the list with other instructions that can be composed from the basic list, such as shift left by a fixed amount (which is equivalent to a sequence of add’s), or multiply. However, we exclude instructions that cannot be composed from the list. The test is contained in the following theorem.
THEOREM. A function mapping words to words can be implemented with word-parallel add, subtract, and, or, and not instructions if and only if each bit of the result depends only on bits at and to the right of each input operand.
That is, imagine trying to compute the rightmost bit of the result by looking only at the rightmost bit of each input operand. Then, try to compute the next bit to the left by looking only at the rightmost two bits of each input operand, and continue in this way. If you are successful in this, then the function can be computed with a sequence of add’s, and’s, and so on. If the function cannot be computed in this right-to-left manner, then it cannot be implemented with a sequence of such instructions.
The interesting part of this is the latter statement, and it is simply the contra-positive of the observation that the functions add, subtract, and, or, and not can all be computed in the right-to-left manner, so any combination of them must have this property.
To see the “if” part of the theorem, we need a construction that is a little awkward to explain. We illustrate it with a specific example. Suppose that a function of two variables x and y has the right-to-left computability property, and suppose that bit 2 of the result r is given by
We number bits from right to left, 0 to 31. Because bit 2 of the result is a function of bits at and to the right of bit 2 of the input operands, bit 2 of the result is “right-to-left computable.”
Arrange the computer words x, x shifted left two, and y shifted left one, as shown below. Also, add a mask that isolates bit 2.
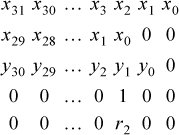
Now, form the word-parallel and of lines 2 and 3, or the result with row 1 (following Equation (1)), and and the result with the mask (row 4 above). The result is a word of all 0’s except for the desired result bit in position 2. Perform similar computations for the other bits of the result, or the 32 resulting words together, and the result is the desired function.
This construction does not yield an efficient program; rather, it merely shows that it can be done with instructions in the basic list.
Using the theorem, we immediately see that there is no sequence of such instructions that turns off the leftmost 1-bit in a word, because to see if a certain 1-bit should be turned off, we must look to the left to see if it is the leftmost one. Similarly, there can be no such sequence for performing a right shift, or a rotate shift, or a left shift by a variable amount, or for counting the number of trailing 0’s in a word (to count trailing 0’s, the rightmost bit of the result will be 1 if there are an odd number of trailing 0’s, and we must look to the left of the rightmost position to determine that).
A Novel Application
An application of the sort of bit twiddling discussed above is the problem of finding the next higher number after a given number that has the same number of 1-bits. You might very well wonder why anyone would want to compute that. It has application where bit strings are used to represent subsets. The possible members of a set are listed in a linear array, and a subset is represented by a word or sequence of words in which bit i is on if member i is in the subset. Set unions are computed by the logical or of the bit strings, intersections by and’s, and so on.
You might want to iterate through all the subsets of a given size. This is easily done if you have a function that maps a given subset to the next higher number (interpreting the subset string as an integer) with the same number of 1-bits.
A concise algorithm for this operation was devised by R. W. Gosper [HAK, item 175].1 Given a word x that represents a subset, the idea is to find the rightmost contiguous group of 1’s in x and the following 0’s, and “increment” that quantity to the next value that has the same number of 1’s. For example, the string xxx0 1111 0000, where xxx represents arbitrary bits, becomes xxx1 0000 0111. The algorithm first identifies the “smallest” 1-bit in x, with s = x &–x, giving 0000 0001 0000. This is added to x, giving r = xxx1 0000 0000. The 1-bit here is one bit of the result. For the other bits, we need to produce a right-adjusted string of n–1 1’s, where n is the size of the rightmost group of 1’s in x. This can be done by first forming the exclusive or of r and x, which gives 0001 1111 0000 in our example.
This has two too many 1’s and needs to be right-adjusted. This can be accomplished by dividing it by s, which right-adjusts it (s is a power of 2), and shifting it right two more positions to discard the two unwanted bits. The final result is the or of this and r.
In computer algebra notation, the result is y in
A complete C procedure is given in Figure 2–1. It executes in seven basic RISC instructions, one of which is division. (Do not use this procedure with x = 0; that causes division by 0.)
If division is slow but you have a fast way to compute the number of trailing zeros function ntz(x), the number of leading zeros function nlz(x), or population count (pop(x) is the number of 1-bits in x), then the last line of Equation (2) can be replaced with one of the following formulas. (The first two methods can fail on a machine that has modulo 32 shifts.)

Figure 2-1. Next higher number with same number of 1-bits.