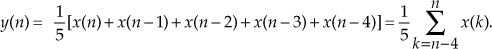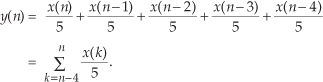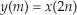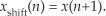Understanding Digital Signal Processing: Discrete Sequences and Systems

This chapter is from the book

Understanding Digital Signal Processing, 3rd Edition

Learn More Buy

This chapter is from the book

This chapter is from the book 

Understanding Digital Signal Processing, 3rd Edition

Learn More Buy

Chapter 1 Problems

• 1.1 This problem gives us practice in thinking about sequences of numbers. For centuries mathematicians have developed clever ways of computing p. In 1671 the Scottish mathematician James Gregory proposed the following very simple series for calculating p:

  

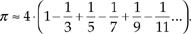
  Thinking of the terms inside the parentheses as a sequence indexed by the variable n, where n = 0, 1, 2, 3, . . ., 100, write Gregory's algorithm in the form

  

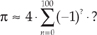
  replacing the "?" characters with expressions in terms of index n.

• 1.2 One of the ways to obtain discrete sequences, for follow-on processing, is to digitize a continuous (analog) signal with an analog-to-digital (A/D) converter. A 6-bit A/D converter's output words (6-bit binary words) can only represent 2⁶ = 64 different numbers. (We cover this digitization, sampling, and A/D converters in detail in upcoming chapters.) Thus we say the A/D converter's "digital" output can only represent a finite number of amplitude values. Can you think of a continuous time-domain electrical signal that only has a finite number of amplitude values? If so, draw a graph of that continuous-time signal.

• 1.3 On the Internet, the author once encountered the following line of C-language code

  PI = 2*asin(1.0);

  whose purpose was to define the constant p. In standard mathematical notation, that line of code can be described by

  p = 2 · sin^–1(1).

  Under what assumption does the above expression correctly define the constant p?

• 1.4 Many times in the literature of signal processing you will encounter the identity

  x⁰ = 1.

  That is, x raised to the zero power is equal to one. Using the Laws of Exponents, prove the above expression to be true.

• 1.5 Recall that for discrete sequences the t_s sample period (the time period between samples) is the reciprocal of the sample frequency f_s. Write the equations, as we did in the text's Eq. (1–3), describing time-domain sequences for unity-amplitude cosine waves whose f_o frequencies are

  1. f_o = f_s/2, one-half the sample rate,
  2. f_o = f_s/4, one-fourth the sample rate,
  3. f_o = 0 (zero) Hz.
• 1.6 Draw the three time-domain cosine wave sequences, where a sample value is represented by a dot, described in Problem 1.5. The correct solution to Part (a) of this problem is a useful sequence used to convert some lowpass digital filters into highpass filters. (Chapter 5 discusses that topic.) The correct solution to Part (b) of this problem is an important discrete sequence used for frequency translation (both for signal down-conversion and up-conversion) in modern-day wireless communications systems. The correct solution to Part (c) of this problem should convince us that it's perfectly valid to describe a cosine sequence whose frequency is zero Hz.

• 1.7 Draw the three time-domain sequences of unity-amplitude sinewaves (not cosine waves) whose frequencies are

  1. f_o = f_s/2, one-half the sample rate,
  2. f_o = f_s/4, one-fourth the sample rate,
  3. f_o = 0 (zero) Hz.

  The correct solutions to Parts (a) and (c) show us that the two frequencies, 0 Hz and f_s/2 Hz, are special frequencies in the world of discrete signal processing. What is special about the sinewave sequences obtained from the above Parts (a) and (c)?

• 1.8 Consider the infinite-length time-domain sequence x(n) in Figure P1–8. Draw the first eight samples of a shifted time sequence defined by

  x_shift(n) = x(n+1).

  

  Figure P1–8

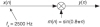
• 1.9 Assume, during your reading of the literature of DSP, you encounter the process shown in Figure P1–9. The x(n) input sequence, whose f_s sample rate is 2500 Hz, is multiplied by a sinusoidal m(n) sequence to produce the y(n) output sequence. What is the frequency, measured in Hz, of the sinusoidal m(n) sequence?

  

  Figure P1–9

• 1.10 There is a process in DSP called an "N-point running sum" (a kind of digital lowpass filter, actually) that is described by the following equation:

  

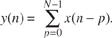
  Write out, giving the indices of all the x() terms, the algebraic expression that describes the computations needed to compute y(9) when N = 6.

• 1.11 A 5-point moving averager can be described by the following difference equation:

  Equation P1–1

  

  The averager's signal-flow block diagram is shown in Figure P1–11, where the x(n) input samples flow through the averager from left to right.

  

  Figure P1–11

  Equation (P1–1) is equivalent to

  Equation P1–2

  

  1. Draw the block diagram of the discrete system described by Eq. (P1–2).
  2. The moving average processes described by Eqs. (P1–1) and (P1–2) have identical impulse responses. Draw that impulse response.
  3. If you had to implement (using programmable hardware or assembling discrete hardware components) either Eq. (P1–1) or Eq. (P1–2), which would you choose? Explain why.

• 1.12 In this book we will look at many two-dimensional drawings showing the value of one variable (y) plotted as a function of another variable (x). Stated in different words, we'll graphically display what are the values of a y axis variable for various values of an x axis variable. For example, Figure P1–12(a) plots the weight of a male child as a function of the child's age. The dimension of the x axis is years and the dimension of the y axis is kilograms. What are the dimensions of the x and y axes of the familiar two-dimensional plot given in Figure P1–12(b)?

  

  Figure P1–12

• 1.13 Let's say you are writing software code to generate an x(n) test sequence composed of the sum of two equal-amplitude discrete cosine waves, as

  x(n) = cos(2pf_ont_s + f) + cos(2pf_ont_s)

  where t_s is the time between your x(n) samples, and f is a constant phase shift measured in radians. An example x(n) when f = p/2 is shown in Figure P1–13 where the x(n) sequence, represented by the circular dots, is a single sinusoid whose frequency is f_o Hz.

  

  Figure P1–13

  Using the trigonometric identity cos(a+b) + cos(a–b) = 2cos(a)cos(b), derive an equation for x(n) that is of the form

  x(n) = 2cos(a)cos(b)

  where variables a and b are in terms of 2pf_ont_s and f.

• 1.14 In your engineering education you'll often read in some mathematical derivation, or hear someone say, "For small a, sin(a) = a." (In fact, you'll encounter that statement a few times in this book.) Draw two curves defined by

  x = a, and y = sin(a)

  over the range of a = –p/2 to a = p/2, and discuss why that venerable "For small a, sin(a) = a" statement is valid.

• 1.15 Considering two continuous (analog) sinusoids, having initial phase angles of a radians at time t = 0, replace the following "?" characters with the correct angle arguments:

  1. sin(2pf_ot + a) = cos(?).
  2. cos(2pf_ot + a) = sin(?).
• 1.16 National Instruments Corp. manufactures an A/D converter, Model #NI USB-5133, that is capable of sampling an analog signal at an f_s sample rate of 100 megasamples per second (100 MHz). The A/D converter has internal memory that can store up to 4x10⁶ discrete samples. What is the maximum number of cycles of a 25 MHz analog sinewave that can be stored in the A/D converter's memory? Show your work.

• 1.17 In the first part of the text's Section 1.5 we stated that for a process (or system) to be linear it must satisfy a scaling property that we called the proportionality characteristic in the text's Eq. (1–14). Determine if the following processes have that proportionality characteristic:

  1. y_a(n) = x(n–1)/6,
  2. y_b(n) = 3 + x(n),
  3. y_c(n) = sin[x(n)].

  This problem is not "busy work." Knowing if a process (or system) is linear tells us what signal processing principles, and algorithms, can be applied in the analysis of that process (or system).

• 1.18 There is an often-used process in DSP called decimation, and in that process we retain some samples of an x(n) input sequence and discard other x(n) samples. Decimation by a factor of two can be described algebraically by

  Equation P1–3

  

  where index m = 0,1,2,3,. . . The decimation defined by Eq. (P1–3) means that y(m) is equal to alternate samples (every other sample) of x(n). For example:

  y(0) = x(0), y(1) = x(2), y(2) = x(4), y(3) = x(6), . . .

  and so on. Here is the question: Is that decimation process time invariant? Illustrate your answer by decimating a simple sinusoidal x(n) time-domain sequence by a factor of two to obtain y(m). Next, create a shifted-by-one-sample version of x(n) and call it x_shift(n). That new sequence is defined by

  Equation P1–4

  

  Finally, decimate x_shift(n) according to Eq. (P1–3) to obtain y_shift(m). The decimation process is time invariant if y_shift(m) is equal to a time-shifted version of y(m). That is, decimation is time invariant if

  y_shift(m) = y(m+1).

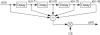
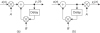
• 1.19 In Section 1.7 of the text we discussed the commutative property of linear time-invariant systems. The two networks in Figure P1–19 exhibit that property. Prove this to be true by showing that, given the same x(n) input sequence, outputs y₁(n) and y₂(n) will be equal.

  

  Figure P1–19

• 1.20 Here we investigate several simple discrete processes that turn out to be useful in a number of DSP applications. Draw the block diagrams, showing their inputs as x(n), of the processes described by the following difference equations:

  1. a 4th-order comb filter: y_C(n) = x(n) – x(n–4),
  2. an integrator: y_I(n) = x(n) + y_I(n–1),
  3. a leaky integrator: y_LI(n) = Ax(n) + (1–A)y_LI(n–1) [the scalar value A is a real-valued constant in the range 0 < A < 1],
  4. a differentiator: y_D(n) = 0.5x(n) – 0.5x(n-2).
• 1.21 Draw the unit impulse responses (the output sequences when the input is a unit sample impulse applied at time n = 0) of the four processes listed in Problem 1.20. Let A = 0.5 for the leaky integrator. Assume that all sample values within the systems are zero at time n = 0.

• 1.22 DSP engineers involved in building control systems often need to know what is the step response of a discrete system. The step response, y_step(n), can be defined in two equivalent ways. One way is to say that y_step(n) is a system's response to an input sequence of all unity-valued samples. A second definition is that y_step(n) is the cumulative sum (the accumulation, discrete integration) of that system's unit impulse response y_imp(n). Algebraically, this second definition of step response is expressed as

  

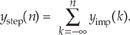
  In words, the above y_step(n) expression tells us: "The step response at time index n is equal to the sum of all the previous impulse response samples up to and including y_imp(n)." With that said, what are the step responses of the four processes listed in Problem 1.20? (Let A = 0.5 for the leaky integrator.) Assume that all sample values within the system are zero at time n = 0.

• 1.23 Thinking about the spectra of signals, the ideal continuous (analog) squarewave s(t) in Figure P1–23, whose fundamental frequency is f_o Hz, is equal to the sum of an f_o Hz sinewave and all sinewaves whose frequencies are odd multiples of f_o Hz. We call s(t) "ideal" because we assume the amplitude transitions from plus and minus A occur instantaneously (zero seconds!). Continuous Fourier analysis of the s(t) squarewave allows us to describe this sum of frequencies as the following infinite sum:

  

  

  Figure P1–23

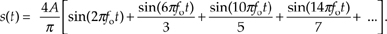
  Using a summation symbol, we can express squarewave s(t) algebraically as

  

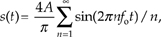
  for n = odd integers only, showing s(t) to be an infinite sum of sinusoids.

  1. Imagine applying s(t) to a filter that completely removes s(t)'s lowest-frequency spectral component. Draw the time-domain waveform at the output of such a filter.
  2. Assume s(t) represents a voltage whose f _o fundamental frequency is 1 Hz, and we wish to amplify that voltage to peak amplitudes of ±2A. Over what frequency range must an amplifier operate (that is, what must be the amplifier's passband width) in order to exactly double the ideal 1 Hz squarewave's peak-peak amplitude?

• 1.24 This interesting problem illustrates an illegal mathematical operation that we must learn to avoid in our future algebraic activities. The following claims to be a mathematical proof that 4 = 5. Which of the following steps is illegal? Explain why.

  Proof that 4 = 5:

  • Step 1: 16 – 36 = 25 – 45
  • Step 2: 4² – 9 · 4 = 5² – 9 · 5
  • Step 3: 4² – 9 · 4 + 81/4 = 5² – 9 · 5 + 81/4
  • Step 4: (4 – 9/2)² = (5 – 9/2)²
  • Step 5: 4 – 9/2 = 5 – 9/2
  • Step 6: 4 = 5