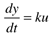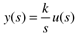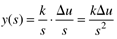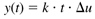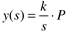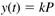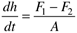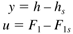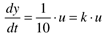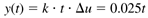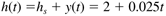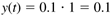- Background
- Linear State Space Models
- Introduction to Laplace Transforms
- Transfer Functions
- First-Order Behavior
- Integrating System
- Second-Order Behavior
- Lead-Lag Behavior
- Poles and Zeros
- Processes with Dead Time
- Padé Approximation for Dead Time
- Converting State Space Models to Transfer Functions
- Matlab and Simulink
- Summary
- References
- Student Exercises
This chapter is from the book
This chapter is from the book
This chapter is from the book
3.6 Integrating System
We found in the previous chapter that material balances on liquid surge vessels or gas drums often yielded models with the following form:
)
In the Laplace domain, this is
)
Consider an integrating process initially at steady state, with y(0) = 0.
Step Response
If a step input change of Du is made at t = 0,
)
and we find the time-domain value
)
That is, the output ramps with a constant slope of kDu.
Impulse Response
If an impulse input of magnitude P is made at t = 0,
)
then the output immediately changes to a new steady-state value of
)
Example 3.5: Tank-Height Problem
The mathematical model for a liquid surge tank is (see Example 1.3)
)
where h is the liquid height, A is the constant cross-sectional area of the tank, F1 is the inlet flow rate, and F2 is the outlet flow rate. Assume that the outlet flow rate remains constant at a steady-state value of F2s. Defining the output and input in deviation variable form as
)
For a constant cross-sectional area of 10 m2, the model is
)
Step Response
For a step input change of 0.25 m3/min, the output response is
)
which is shown in Figure 3-7. If the steady-state height is 2 meters, then the height as a function of time is
)
)
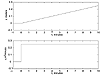Figure 3-7. Step response of a liquid surge tank. Deviation variables.
Impulse Response
For an impulse input of 1 m3, the output response is
)
which makes sense, because the cross-sectional area is 10 m3.