Regression Using Bayesian Methods
Depending on the context, regression can imply a variety of statistical and methodological purposes.
Statisticians use the term regression pretty loosely.
At its simplest, the term refers to the average of the products of the corresponding z-scores—a.k.a., the Pearson correlation coefficient. At its oldest, the term refers to the tendency of sons’ heights to regress toward the mean of their fathers’ heights. When applied to categories such as method of transportation, brand of car, or the presence of a defect in a manufactured product, it’s usually called logistic regression. When particular types of coding schemes are applied to independent variables, which are manipulated by the researcher and not merely observed, it’s often termed the general linear model. And in a true experimental design, the purpose of regression analysis is not simply to predict but, more typically, to explain. Depending on the context, then, regression can imply a variety of statistical and methodological purposes.
Regression à la Bayes
So it shouldn’t be at all surprising that the Bayesian approach to regression looks very different from the frequentist approach. Suppose that you want to better understand the relationship between the amount of fat consumed by adults during a year and the amount of low density lipoproteins (LDL) cholesterol found in blood samples from similar adults at the year’s end.
Assuming that you have no insurmountable difficulties with the acquisition of good data, you’re set up to quantify the relationship between LDL and fat consumption. Just about any application designed to return numeric analyses will provide you with the summary statistics you’re after:
Correlation coefficient. A number between –1.0 and +1.0 that expresses the direction and the strength of relationship between two variables. A correlation of 1.0 describes a perfect and positive relationship, such as height in inches with height in centimeters. A correlation of –1.0 describes a perfect negative relationship. An example of a perfect negative relationship is the correlation between the number of correct answers on a test with the number of incorrect answers on that same test.
R2. The square of the correlation between a predicted variable and one or more predictor variables. I believe that usage calls for the abbreviation to be capitalized (R2) with more than one predictor, and lowercase (r2) with just one predictor.
Slope or regression coefficient. The gradient of a line that shows where x-values, such as golf score, connect with predicted y-values, such as years playing golf (see Figure 6.1). You may recall this concept as taught in middle school as “the rise over the run.”
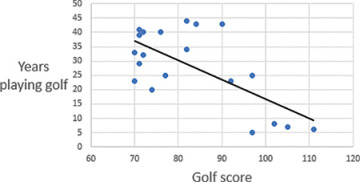
Figure 6.1 A regression line slopes up when the correlation is positive, such as calories consumed and weight. It slopes down, as here, when the correlation is negative, such as number of years playing golf and average golf score.
All of the just-named statistics—and more—are returned by any credible statistics package, certainly various packages supplied by R and even the venerable BMD and Lotus 1-2-3. What distinguishes the Bayesian approach to regression analysis is that it does not maximize or minimize the value of some function such as R2 to arrive at a solution; that is the goal of frequentist approaches. Bayesian methods seek to maximize the probabilities of particular outcomes.
One of the names for frequentist regression is least squares analysis. The frequentist algorithms calculate the combination of predictors that minimizes the squared deviations of the observed predictor variable’s values from the predicted values. The values of the remaining statistics flow from that finding: R2, the F ratio, the standard errors of the intercept and the coefficients, the standard error of estimate, and so on.
The least squares approach to regression analysis works with one, two, three, or more predictor variables. Regression’s job is to combine those predictors to create a new variable. They are combined by multiplying each predictor by its own coefficient, then summing the products of the predictors and their coefficients. Regression does the heavy lifting when it optimizes those coefficients.
Then, regression calculates the correlation between, on one hand, the observed or outcome variable, and on the other hand, the combined predictor variables. Make one tiny change to the value of one of the predictor variables—say, change it from 5.00 to 5.01—and typically all the other variables change in response: their regression coefficients, the standard errors of the regression coefficients, R2, the F ratio, the sums of squares—anything except the degrees of freedom.
Figure 6.2 shows an example.
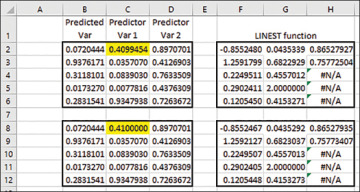
Figure 6.2 The values in the range B2:D6 are identical to those in B8:D12 with one exception: the value in C2 has been changed from 0.4099 to 0.4100 in cell C8. But the regression statistics in F2:H6 are all different from those in F8:H12, with the exception of the degrees of freedom regression.