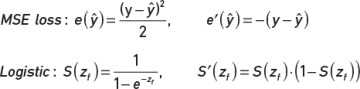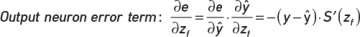- Programming Example: Moving to a DL Framework
- The Problem of Saturated Neurons and Vanishing Gradients
- Initialization and Normalization Techniques to Avoid Saturated Neurons
- Cross-Entropy Loss Function to Mitigate Effect of Saturated Output Neurons
- Different Activation Functions to Avoid Vanishing Gradient in Hidden Layers
- Variations on Gradient Descent to Improve Learning
- Experiment: Tweaking Network and Learning Parameters
- Hyperparameter Tuning and Cross-Validation
- Concluding Remarks on the Path Toward Deep Learning
Cross-Entropy Loss Function to Mitigate Effect of Saturated Output Neurons
One reason for saturation is that we are trying to make the output neuron get to a value of 0 or 1, which itself drives it to saturation. A simple trick introduced by LeCun, Bottou, Orr, and Müller (1998) is to instead set the desired output to 0.1 or 0.9, which restricts the neuron from being pushed far into the saturation region. We mention this technique for historical reasons, but a more mathematically sound technique is recommended today.
We start by looking at the first couple of factors in the backpropagation algorithm; see Chapter 3, Equation 3-1(1) for more context. The formulas for the MSE loss function, the logistic sigmoid function, and their derivatives for a single training example are restated here:2
We then start backpropagation by using the chain rule to compute the derivative of the loss function and multiply by the derivative of the logistic sigmoid function to arrive at the following as the error term for the output neuron:
We chose to not expand S'(zf) in the expression because it makes the formula unnecessarily cluttered. The formula reiterates what we stated in one of the previous sections: that if S'(zf) is close to 0, then no error will backpropagate through the network. We show this visually in Figure 5-4. We simply plot the derivative of the loss function and the derivative of the logistic sigmoid function as well as the product of the two. The chart shows these entities as functions of the output value y (horizontal axis) of the output neuron. The chart assumes that the desired output value (ground truth) is 0. That is, at the very left in the chart, the output value matches the ground truth, and no weight adjustment is needed.

FIGURE 5-4 Derivatives and error term as function of neuron output when ground truth y (denoted y_target in the figure) is 0
As we move to the right in the chart, the output is further away from the ground truth, and the weights need to be adjusted. Looking at the figure, we see that the derivative of the loss function (blue) is 0 if the output value is 0, and as the output value increases, the derivative increases. This makes sense in that the further away from the true value the output is, the larger the derivative will be, which will cause a larger error to backpropagate through the network. Now look at the derivative of the logistic sigmoid function. It also starts at 0 and increases as the output starts deviating from 0. However, as the output gets closer to 1, the derivative is decreasing again and starts approaching 0 as the neuron enters its saturation region. The green curve shows the resulting product of the two derivatives (the error term for the output neuron), and it also approaches 0 as the output approaches 1 (i.e., the error term becomes 0 when the neuron saturates).
Looking at the charts, we see that the problem arises from the combination of the derivative of the activation function approaching 0, whereas the derivative of the loss function never increases beyond 1, and multiplying the two will therefore approach 0. One potential solution to this problem is to use a different loss function whose derivative can take on much higher values than 1. Without further rationale at this point, we introduce the function in Equation 5-1 that is known as the cross-entropy loss function:
Cross entropy loss: e(ŷ) = –(y · ln(ŷ) + (1 – y) · ln(1 – ŷ))
Equation 5-1 Cross-entropy loss function
Substituting the cross-entropy loss function into our expression for the error term of the output neuron yields Equation 5-2:
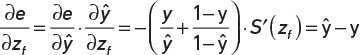
Equation 5-2 Derivative of cross-entropy loss function and derivative of logistic output unit combined into a single expression
We spare you from the algebra needed to arrive at this result, but if you squint your eyes a little bit and remember that the logistic sigmoid function has some ex terms, and we know that ln(ex) = x and the derivative of ln(x) = x−1, then it does not seem farfetched that our seemingly complicated formulas might end up as something as simple as that. Figure 5-5 shows the equivalent plot for these functions. The y-range is increased compared to Figure 5-4 to capture more of the range of the new loss function. Just as discussed, the derivative of the cross-entropy loss function does increase significantly at the right end of the chart, and the resulting product (the green line) now approaches 1 in the case where the neuron is saturated. That is, the backpropagated error is no longer 0, and the weight adjustments will no longer be suppressed.
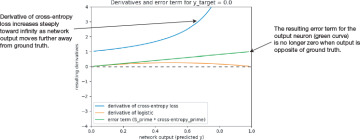
FIGURE 5-5 Derivatives and error term when using cross-entropy loss function. Ground truth y (denoted y_target in the figure) is 0, as in Figure 5-4.
Although the chart seems promising, you might feel a bit uncomfortable to just start using Equation 5-2 without further explanation. We used the MSE loss function in the first place, you may recall, on the assumption that your likely familiarity with linear regression would make the concept clearer. We even stated that using MSE together with the logistic sigmoid function is not a good choice.
We have now seen in Figure 5-4 why this is the case. Still, let us at least give you some insight into why using the cross-entropy loss function instead of the MSE loss function is acceptable. Figure 5-6 shows how the value of the MSE and cross-entropy loss function varies as the output of the neuron changes from 0 to 1 in the case of a ground truth of 0. As you can see, as y moves further away from the true value, both MSE and the cross-entropy function increase in value, which is the behavior that we want from a loss function.
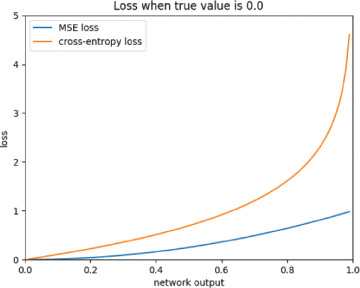
FIGURE 5-6 Value of the mean squared error (blue) and cross-entropy loss (orange) functions as the network output ŷ changes (horizontal axis). The assumed ground truth is 0.
Intuitively, by looking at the chart in Figure 5-6, it is hard to argue that one function is better than the other, and because we have already shown in Figure 5-4 that MSE is not a good function, you can see the benefit of using the cross-entropy loss function instead. One thing to note is that, from a mathematical perspective, it does not make sense to use the cross-entropy loss function together with a tanh neuron because the logarithm for negative numbers is not defined.
In the preceding examples, we assumed a ground truth of 0. For completeness, Figure 5-7 shows how the derivatives behave in the case of a ground truth of 1.
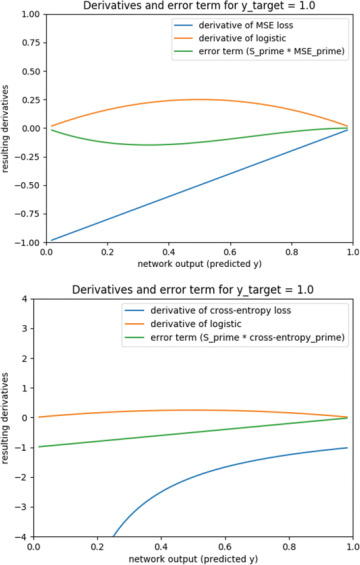
FIGURE 5-7 Behavior of the different derivatives when assuming a ground truth of 1. Top: Mean squared error loss function. Bottom: Cross-entropy loss function.
The resulting charts are flipped in both directions, and the MSE function shows exactly the same problem as for the case when ground truth was 0. Similarly, the cross-entropy loss function solves the problem in this case as well.
Computer Implementation of the Cross-Entropy Loss Function
If you find an existing implementation of a code snippet that calculates the cross-entropy loss function, then you might be confused at first because it does not resemble what is stated in Equation 5-1. A typical implementation can look like that in Code Snippet 5-8. The trick is that, because we know that y in Equation 5-1 is either 1.0 or 0.0, the factors y and (1-y) will serve as an if statement and select one of the ln statements.
Code Snippet 5-8 Python implementation of the cross-entropy loss function
def cross_entropy(y_truth, y_predict):
if y_truth == 1.0:
return -np.log(y_predict)
else:
return -np.log(1.0-y_predict)
Apart from what we just described, there is another thing to consider when implementing backpropagation using the cross-entropy loss function in a computer program. It can be troublesome if you first compute the derivative of the cross-entropy loss (as in Equation 5-2) and then multiply by the derivative of the activation function for the output unit. As shown in Figure 5-5, in certain points, one of the functions approaches 0 and one approaches infinity, and although this mathematically can be simplified to the product approaching 1, due to rounding errors, a numerical computation might not end up doing the right thing. The solution is to analytically simplify the product to arrive at the combined expression in Equation 5-2, which does not suffer from this problem.
In reality, we do not need to worry about these low-level details because we are using a DL framework. Code Snippet 5-9 shows how we can tell Keras to use the cross-entropy loss function for a binary classification problem. We simply state loss='binary_crossentropy' as an argument to the compile function.
Code Snippet 5-9 Use Cross-Entropy Loss for a Binary Classification Problem in TensorFlow
model.compile(loss='binary_crossentropy',
optimizer = optimizer_type,
metrics =['accuracy'])
In Chapter 6, “Fully Connected Networks Applied to Regression,” we detail the formula for the categorical cross-entropy loss function, which is used for multiclass classification problems. In TensorFlow, it is as simple as stating loss='categorical_crossentropy'.