- 6.1 Further with Quantum Mechanics
- 6.2 Quantum Decoherence
- 6.3 Quantum Electrodynamics
- 6.4 Quantum Chromodynamics
- 6.5 Feynman Diagram
- 6.6 Summary
- Test Your Skills
This chapter is from the book
This chapter is from the book
This chapter is from the book
6.3 Quantum Electrodynamics
Quantum electrodynamics (QED) is a topic that may be considered too advanced for an introductory book. The goal is simply for you to acquire a generalized understanding of the topic, and I believe that is an achievable goal. QED is the relativistic quantum field theory that applies to electrodynamics. It is the first theory wherein quantum mechanics and relativity are in full agreement. QED provides a mathematical description of phenomena that involve electrically charged particles.
Let us begin by defining the quantum field theory (QFT). QFT combines classical field theory, special relativity, and quantum mechanics. At this point, you should have a general working knowledge of quantum mechanics. Therefore, we will turn our attention to classical field theory and special relativity, providing a brief description of each.
Classical field theory describes how one or more fields interact with matter, via field equations. An easy-to-understand example is with weather patterns. The wind velocity at a given time can be described by a vector. Each vector describes the direction and movement of the air at a particular point. The set of all such vectors in a particular area at a given point in time would be a vector field. Over time, we would expect these vectors to change. This is the essence of a classical field theory. Maxwell’s equations of electromagnetic fields were among the first rigorous field theories.
Special relativity is something you are likely familiar with. In case you need a bit of a refresher, it essentially gives us two concepts. The first is that the laws of physics are invariant; there are no privileged reference points. Also, the speed of light in a vacuum is constant.
The development of quantum electrodynamics began with the study of the interaction between light and electrons. When this research began, the only field known was the electromagnetic field, so it was an obvious place to begin. The term quantum electrodynamics was posited by Paul Dirac in 1927 in his paper “The quantum theory of the emission and absorption of radiation.”
Classical electromagnetism would describe the force between two electrons as being an electric field produced by each electron’s position. The force itself can be calculated using Coulomb’s law. However, quantum field theory visualizes the force between electrons arising from the exchange of virtual photons.
Quantum electrodynamics is the fundamental theory that describes the interaction of light and matter. To be a bit more mathematically robust, the charged particles that provide the source for the electromagnetic fields are described by relativistic equations of motion (more specifically, the Klein-Gordon equation for integer spin and the Dirac equation for a spin). Let us briefly examine these equations. Keep in mind that for the purposes of this book, you need not become an expert in these equations. You only need a general understanding of what they do.
Klein-Gordon is a relativistic wave equation that is actually related to the Schrödinger equation, so it will at least look a bit familiar to you. Equation 6.10 provides the equation.
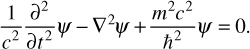
EQUATION 6.10 Klein-Gordon Equation
Now, much of this you already know. Refreshing your memory a bit, ψ is the wave function,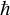 
is the reduced Planck constant, and m is mass. We have also discussed second derivatives and partial differential equations previously in this book. The c is the velocity of light in centimeters per second. I think you can already see some connection between this and Einstein’s famous E = mc2. I have yet to explain one other symbol, ∇. This one actually shows up frequently in quantum physics. This is the Laplace operator, sometimes called the Laplacian. It is sometimes denoted by ∇ ∇ and sometimes by ∇2. The definition of the Laplacian might seem a bit confusing to you. It is a second-order differential operator defined as the divergence of the gradient. In this case, the term gradient is a vector calculus term. It refers to a scalar-valued function f of several variables that is the vector field. The Laplacian of that vector field at some point is the vector whose components are partial derivatives of the function f at point p.
Hopefully, this general explanation did not leave you totally confused. Recall from the introduction that you need not master all of the mathematics presented in this chapter. Just make sure you understand the general idea. So what is that general idea? The Klein-Gordon equation is a relativistic wave function that describes the motion for the field, as it varies in time and space.
The Dirac equation for the spin is also a relativistic wave function. It describes particles such as electrons and quarks. It should be noted that electrons and quarks are the particles that constitute ordinary matter and are known as fermions. We will have much more to say about quarks in the section on quantum chromodynamics. The spin number describes how many symmetrical facets a particle has in one full rotation. Thus, a spin of 1/2 means the particle has to be rotated twice (i.e., 720 degrees) before it has the same configuration as when it started. Protons, neutrons, electrons, neutrinos, and quarks all have a spin of 1/2, and that is enough for you to move forward with the rest of this book. However, for some readers, you not only want to see more of the math, but by this point in this text you have become accustomed to it. So, in the interest of not disappointing those readers, Equation 6.11 presents the Dirac equation as Paul Dirac originally proposed it.
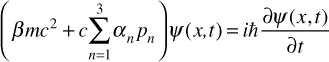
EQUATION 6.11 Dirac Equation
Again, you see the now-familiar partial differential symbol, the reduced Planck constant, and the wave function—all of which should be quite familiar to you by now. You also see mc2, and I anticipate most readers realize this is mass and the velocity of light, just as it is in E = mc2. In this equation, the x and t are space and time coordinates, respectively. The p values that are being summed (p1, p2, and p3) are components of the momentum. The symbols α and β are 4 × 4 matrices. These are 4 × 4 matrices because they have four complex components (i.e. using complex numbers). Such objects are referred to in physics as a bispinor.
After our rather extensive excursions into the math of QED, let us complete this section with a return to the essential facts of QED. Electrodynamics, as the name suggests, is concerned with electricity. However, quantum electrodynamics provides a relativistic explanation of how light and matter interact. It is used to understand the interactions among electrically charged elementary particles, at a fundamental level. It is a very important part of quantum physics.