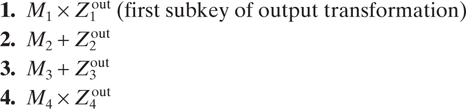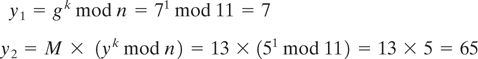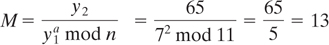This chapter is from the book
This chapter is from the book
This chapter is from the book
17.6 Pretty Good Privacy
Pretty Good Privacy (PGP) is a security program that was created by Phil Zimmerman [17] and published in 1991 as free-of-charge shareware. It has since become the “de facto” standard for electronic mail (e-mail) and file encryption. PGP, widely used as version 2.6, remained essentially unchanged until PGP version 5.0 (which is compatible with version 2.6) became available. Table 17.9 illustrates the algorithms used in versions 2.6, 5.0, and later.
Table 17.9 PGP 2.6 versus PGP 5.0 and Later
Function |
PGP Version 2.6 Algorithm Used [17] |
PGP Version 5.0 and Later Algorithm Used [18] |
|---|---|---|
Encryption of message using private-key algorithm with private-session key |
IDEA |
Triple-DES, CAST, or IDEA |
Encryption of private-session key with public-key algorithm |
RSA |
RSA or Diffie-Hellman (the Elgamal variation) |
Digital Signature |
RSA |
|
Hash Function used for creating message digest for Digital Signatures |
MD5 |
SHA-1 |
As listed in Table 17.9, PGP uses a variety of encryption algorithms, including both private-key- and public-key-based systems. A private-key algorithm (with a new session key generated at each session) is used for encryption of the message. The private-key algorithms offered by PGP are International Data Encryption Algorithm (IDEA), Triple-DES (Data Encryption Standard), and CAST (named after the inventors Carlisle Adams and Stafford Tavares [19]). A public-key algorithm is used for the encryption of each session key. The public-key algorithms offered by PGP are the RSA algorithm, described in Section 17.5.3, and the Diffie-Hellman algorithm.
Public-key algorithms are also used for the creation of digital signatures. PGP version 5.0 uses the Digital Signature Algorithm (DSA) specified in the NIST Digital Signature Standard (DSS). PGP version 2.6 uses the RSA algorithm for its digital signatures. If the available channel is insecure for key exchange, it is safest to use a public-key algorithm. If a secure channel is available, then private-key encryption is preferred, since it typically offers improved speed over public-key systems.
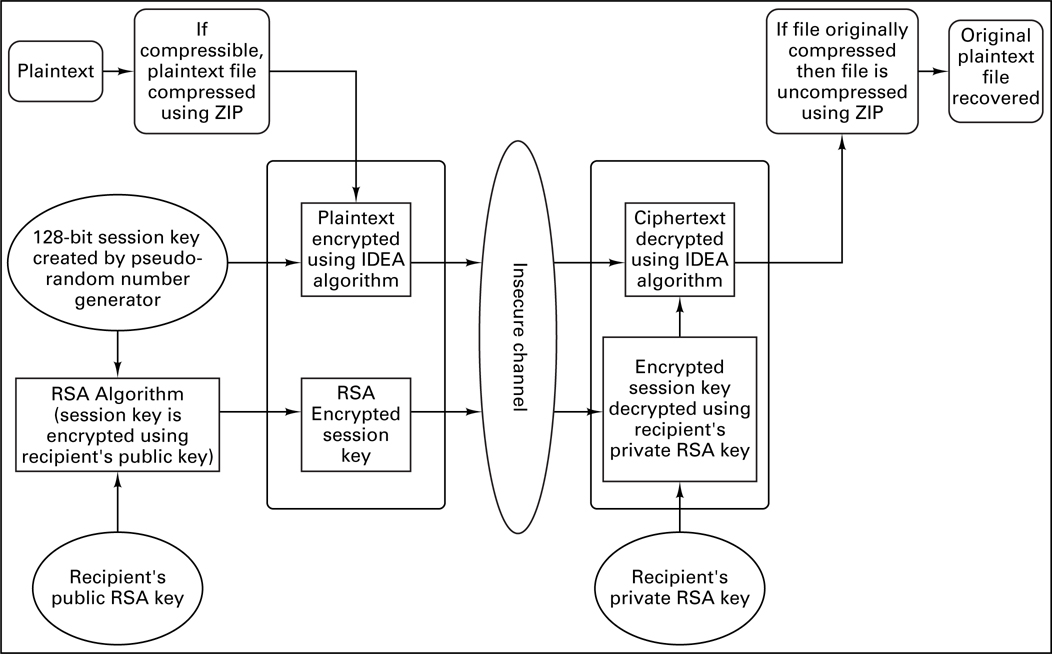
The technique for message encryption employed by PGP version 2.6 is illustrated in Figure 17.20. The plaintext is compressed with the ZIP algorithm prior to encryption. PGP uses the ZIP routine written by Jean-Loup Gailly, Mark Alder, and Richard B. Wales [18]. If the compressed text is shorter than the uncompressed text, the compressed text will be encrypted; otherwise the uncompressed text is encrypted.
)
Small files (approximately 30 characters for ASCII files) will not benefit from compression. Additionally, PGP recognizes files previously compressed by popular compression routines, such as PKZIP, and will not attempt to compress them. Data compression removes redundant character strings in a file and produces a more uniform distribution of characters. Compression provides a shorter file to encrypt and decrypt (which reduces the time needed to encrypt, decrypt, and transmit a file), but compression is also advantageous because it can hinder some cryptanalytic attacks that exploit redundancy. If compression is performed on a file, it should occur prior to encryption (never afterwards). Why is that a good rule to follow? Because a good encryption algorithm yields ciphertext with a nearly statistically uniform distribution of characters; therefore, if a data compression algorithm came after such encryption, it should result in no compression at all. If any ciphertext can be compressed, then the encryption algorithm that formed that ciphertext was a poor algorithm. A compression algorithm should be unable to find redundant patterns in text that was encrypted by a good encryption algorithm.
As shown in Figure 17.20, PGP Version 2.6 begins file encryption by creating a 128-bit session key using a pseudo-random number generator. The compressed plaintext file is then encrypted with the IDEA private-key algorithm using this random session key. The random session key is then encrypted by the RSA public-key algorithm using the recipient’s public key. The RSA-encrypted session key and the IDEA-encrypted file are sent to the recipient. When the recipient needs to read the file, the encrypted session key is first decrypted with RSA using the recipient’s private key. The ciphertext file is then decrypted with IDEA using the decrypted session key. After uncompression, the recipient can read the plaintext file.
17.6.1 Triple-DES, CAST, and IDEA
As listed in Table 17.9, PGP offers three block ciphers for message encryption, Triple-DES, CAST, and IDEA. All three ciphers operate on 64-bit blocks of plaintext and ciphertext. Triple-DES has a key size of 168-bits, while CAST and IDEA use key lengths of 128 bits.
17.6.1.1 Description of Triple-DES
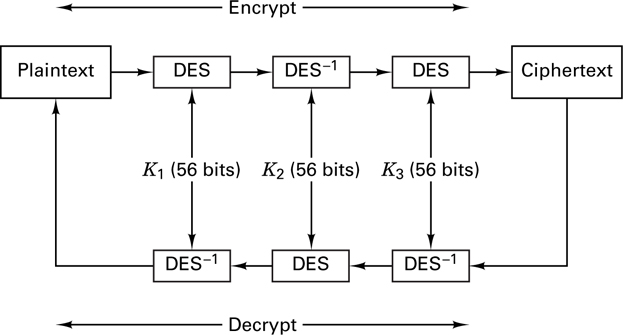
The Data Encryption Standard (DES) described in Section 17.3.5 has been used since the late 1970s, but some have worried about its security because of its relatively small key size (56 bits). With Triple-DES, the message to be encrypted is run through the DES algorithm 3 times (the second DES operation is run in decrypt mode); each operation is performed with a different 56-bit key. As illustrated in Figure 17.21, this gives the effect of a 168-bit key length.
)
17.6.1.2 Description of CAST
CAST is a family of block ciphers developed by Adams and Tavares [19]. PGP version 5.0 uses a version of CAST known as CAST5, or CAST-128. This version has a block size of 64-bits and a key length of 128-bits. The CAST algorithm uses six S-boxes with an 8-bit input and a 32-bit output. By comparison, DES uses eight S-boxes with a 6-bit input and a 4-bit output. The S-boxes in Cast-128 were designed to provide highly nonlinear transformations, making this algorithm particularly resistant to cryptanalysis [11].
17.6.1.3 Description of IDEA
The International Data Encryption Algorithm (IDEA) is a block cipher designed by Xuejia Lai and James Massey [19]. It is a 64-bit iterative block cipher (involving eight iterations or rounds) with a 128-bit key. The security of IDEA relies on the use of three types of arithmetic operations on 16-bit words. The operations are addition modulo 216, multiplication modulo 216 + 1, and bit-wise exclusive-OR (XOR). The 128-bit key is used for the iterated encryption and decryption in a reordered fashion. As shown in Table 17.10, the original key K0 is divided into eight 16-bit subkeys Zx(R), where x is the subkey number of the round R. Six of these sub-keys are used in round 1, and the remaining two are used in round 2. K0 is then rotated 25 bits to the left yielding K1, which is in turn divided into eight subkeys; the first 4 of these subkeys are used in round 2, and the last four in round 3. The process continues, as shown in Table 17.10, yielding a total of 52 subkeys.
Table 17.10 IDEA formation of Subkeys
128-bit key (divided into eight 16-bit subkeys) |
Bit string from which keys are derived |
|---|---|
Z11 Z21 Z31 Z41 Z51 Z61 Z12 Z22 |
K0 = Original 128-bit key |
Z32 Z42 Z52 Z62 Z13 Z23 Z33 Z43 |
K1 = 25-bit rotation of K0 |
Z53 Z63 Z14 Z24 Z34 Z44 Z54 Z64 |
K2 = 25-bit rotation of K1 |
Z15 Z25 Z35 Z45 Z55 Z65 Z16 Z26 |
K3 = 25-bit rotation of K2 |
Z36 Z46 Z56 Z66 Z17 Z27 Z37 Z47 |
K4 = 25-bit rotation of K3 |
Z57 Z67 Z18 Z28 Z38 Z48 Z58 Z68 |
K5 = 25-bit rotation of K |
4 Z1out Z2out Z3out Z4out |
First 64 bits of K6 where K6 = 25-bit rotation of K5 |
The subkey schedule for each round is listed in Table 17.11 for both encryption and decryption rounds. Decryption is carried out in the same manner as encryption. The decryption subkeys are calculated from the encryption subkeys, as shown in Table 17.11, where it is seen that the decryption subkeys are either the additive or multiplicative inverses of the encryption subkeys.
Table 17.11 IDEA Subkey Schedule
Round |
Set of Encryption Subkeys |
Set of Decryption Subkeys |
|---|---|---|
1 |
Z11 Z21 Z31 Z41 Z51 Z61 |
(Z1out)- 1 - Z2out - Z3out (Z4out) - 1 Z58 Z68 |
2 |
Z12 Z22 Z32 Z42 Z52 Z62 |
(Z18)- 1 - Z28 - Z38 (Z48)- 1 Z57 Z67 |
3 |
Z13 Z23 Z33 Z43 Z53 Z63 |
(Z17)- 1 - Z27 - Z37 (Z47)- 1 Z56 Z66 |
4 |
Z14 Z24 Z34 Z44 Z54 Z64 |
(Z16)- 1 - Z26 -Z36 (Z46)- 1 Z55 Z65 |
5 |
Z15 Z25 Z35 Z45 Z55Z65 |
(Z15)- 1 - Z25 - Z35 (Z45)- 1 Z54 Z64 |
6 |
Z16 Z26 Z36 Z46 Z56 Z66 |
(Z14)- 1 - Z24 - Z34 (Z44)- 1 Z53 Z63 |
7 |
Z17 Z27 Z37 Z47 Z57 Z67 |
(Z13)- 1 Z23 - Z33 (Z43)- 1 Z52 Z62 |
8 |
Z18 Z28 Z38 Z48 Z58 Z68 |
(Z12)- 1 - Z22 - Z32 (Z42)- 1 Z51 Z61 |
Output |
Z1out Z2out Z3out Z4out |
(Z11)- 1 - Z21 - Z31 (Z41)- 1 |
Transformation |
The message is divided into 64-bit data blocks. These blocks are then divided into four 16-bit subblocks: M1, M2, M3, and M4. A sequence of such four subblocks becomes the input to the first round of IDEA algorithm. This data is manipulated for a total of eight rounds. Each round uses a different set of six subkeys as specified in Table 17.11. After a round, the second and third 16-bit data subblocks are swapped. After the completion of the eighth round, the four subblocks are manipulated in a final output transformation. For the representation of Zx(R) shown in Tables 17.10 and 17.11, the round number is shown without parentheses for ease of notation.
Each round consists of the steps shown in Table 17.12. The final values from steps 11–14 form the output of the round. The two inner 16-bit data subblocks (except for the last round) are swapped, and then these four subblocks are the input to the next round. This technique continues for a total of 8 rounds. After round 8, the final output transformation is as follows:
)
Table 17.12 IDEA Operational Steps in Each Round
|
EXAMPLE 17.8 THE FIRST ROUND OF THE IDEA CIPHER
Consider that the message is the word “HI,” which we first transform to hexadecimal (hex) notation. We start with the ASCII code table in Figure 2.3, where bit 1 is the least significant bit (LSB). We then add an eighth zero-value most significant bit (MSB), which might ordinarily be used for parity, and we transform four bits at a time reading from MSB to LSB. Thus, the letter H in the message transforms to 0048 and the letter I transforms to 0049. For this example, we choose a 128-bit key, K0, expressed with eight groups or subkeys of 4-hex digits each, as follows: K0 = 0008 0007 0006 0005 0004 0003 0002 0001, where the rightmost subkey is the least significant. Using this key and the IDEA cipher, find the output of round 1.
Solution
The message is first divided into 64-bit data blocks. Each of these blocks is then divided into subblocks, Mi, where i = 1,...4, each subblock containing 16-bits or 4-hex digits. In this example the message “HI” is only 16-bits in length, hence (using hex notation) M1 = 4849 and M2 = M3 = M4 = 0000. Addition is performed modulo 216, and multiplication is performed modulo 216 + 1. For the first round, the specified 128-bit key is divided into eight 16-bit subkeys starting with the least significant group of hex digits, as follows: Z1(1) = 0001, Z2(1) = 0002, Z3(1) = 0003, Z4(1) = 0004, Z5(1) = 0005, Z6(1) = 0006, Z1(2) = 0007, and Z2(2) = 0008.
The steps outlined in Table 17.11 yield:
M1 × Z1 = 4849 × 0001 = 4849.
M2 + Z2 = 0000 + 0002 = 0002.
M3 + Z3 = 0000 + 0003 = 0003.
M4 × Z4 = 0000 × 0004 = 0000.
The result from step (1) is XOR’ed with the result from step (3) yielding 4849 XOR 0003 = 484A, as follows:
Converting back to hex yields: 484A (where A is the hex notation for 1010 binary)
Results from steps (2) and (4) are XOR’ed: 0002 XOR 0000 = 0002.
Results from step (5) and Z5 are multiplied: 484A × 0005 = 6971.
Results from steps (6) and (7) are added: 0002 + 6971 = 6973.
Results from step (8) and Z6 are multiplied: 6973 × 0006 = 78B0.
Results from steps (7) and (9) are added: 6971 + 78B0 = E221.
Results from steps (1) and (9) are XOR’ed: 4849 XOR 78B0 = 30F9.
Results from steps (3) and (9) are XOR’ed: 0003 XOR 78B0 = 78B3.
Results from steps (2) and (10) are XOR’ed: 0002 XOR E221 = E223.
Results from steps (4) and (10) are XOR’ed: 0000 XOR E221 = E221.
The output of round 1 (the result from steps 11–14) is: 30F9 78B3 E223 E221. Prior to the start of round 2, the two inner words of the round 1 output are swapped. Then, seven additional rounds and a final output transformation are performed.
17.6.2 Diffie-Hellman (Elgamal Variation) and RSA
For encryption of the session key, PGP offers a choice of two public-key encryption algorithms, RSA and the Diffie-Hellman (Elgamal variation) protocol. PGP allows for key sizes of 1024 to 4096 bits for RSA or Diffie-Hellman algorithms. The key size of 1024 bits is considered safe for exchanging most information. The security of the RSA algorithm (see Section 17.5.3) is based on the difficulty of factoring large integers.
The Diffie-Hellman protocol was developed by Whitfield Diffie, Martin E. Hellman, and Ralph C. Merkle in 1976 [19, 20] for public-key exchange over an insecure channel. It is based on the difficulty of the discrete logarithm problem for finite fields [21]. It assumes that it is computationally infeasible to compute gab knowing only ga and gb. U.S. Patent 4,200,770, which expired in 1997, covers the Diffie-Hellman protocol and variations such as Elgamal. The Elgamal variation, which was developed by Taher Elgamal, extends the Diffie-Hellman protocol for message encryption. PGP employs the Elgamal variation of Diffie-Hellman for the encryption of the session-key.
17.6.2.1 Description of Diffie-Hellman, Elgamal Variant:
The protocol has two-system parameter n and g that are both public. Parameter n is a large prime number, and parameter g is an integer less than n that has the following property: for every number p between 1 and n - 1 inclusive, there is a power k of g such that gk = p mod n. The Elgamal encryption scheme [19, 21] that allows user B to send a message to user A is described below:
User A randomly chooses a large integer, a (this is user A’s private key).
User A’s public key is computed as: y = ga mod n.
User B wishes to send a message M to user A. User B first generates a random number k that is less than n.
User B computes the following:
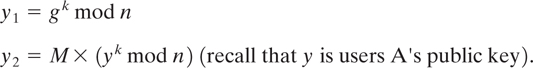
User B sends the ciphertext (y1, y2) to user A.
Upon receiving ciphertext (y1, y2), user A computes the plaintext message M as follows:
EXAMPLE 17.9 DIFFIE-HELLMAN (ELGAMAL VARIATION) FOR MESSAGE ENCRYPTION
Consider that the public-system parameters are n = 11 and g = 7. Suppose that user A chooses the private key to be a = 2. Show how user A’s public key is computed. Also, show how user B would encrypt a message M = 13 to be sent to user A, and how user A subsequently decrypts the ciphertext to yield the message.
Solution
User A’s public key (y = ga mod n) is computed as: y = 72 mod 11 = 5. User B wishes to send message M = 13 to user A. For this example, let user B randomly choose a value of k (less than n = 11) to be k = 1. User B computes the ciphertext pair
User A receives the ciphertext (7, 65), and computes message M as follows:
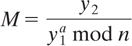
17.6.3 PGP Message Encryption
The private-key algorithms that PGP uses for message encryption were presented in Section 17.6.1. The public-key algorithms that PGP uses to encrypt the private-session key were presented in Section 17.6.2. The next example combines the two types of algorithms to illustrate the PGP encryption technique shown in Figure 17.20.
EXAMPLE 17.10 PGP USE OF RSA AND IDEA FOR ENCRYPTION
For the encryption of the session key, use the RSA public-key algorithm with the parameters taken from Section 17.5.3.1, where n = pq = 2773, the encryption key is e = 17, and the decryption key is d = 157. The encryption key is the recipient’s public key, and the decryption key is the recipient’s private key. From Example 17.8, use the session key K0 = 0008 0007 0006 0005 0004 0003 0002 0001, and the ciphertext of 30F9 78B3 E223 E221 representing the message “HI,” where all the digits are shown in hexadecimal notation. (Note that the ciphertext was created by using only one round of the IDEA algorithm. In the actual implementation, 8 rounds plus an output transformation are performed.) Encrypt the session key, and show the PGP transmission that would be made.
Solution
Following the description in Section 17.5.3.1, the session key will be encrypted using the RSA algorithm with the recipient’s public key of 17. For ease of calculation with a simple calculator, let us first transform the session key into groups made up of base-10 digits. In keeping with the requirements of the RSA algorithm, the value ascribed to any group may not exceed n - 1 = 2772. Therefore, let us express the 128-bit key in terms of 4-digit groups, where we choose the most significant group (leftmost) to represent 7 bits, and the balance of the 11 groups to represent 11 bits each. The transformation from base-16 to base-10 digits can best be viewed as a two-step process, (1) conversion to binary and (2) conversion to base 10. The result is K0 = 0000 0032 0000 1792 0048 0001 0512 0064 0001 1024 0064 0001. Recall from Equation 17.32 that C = (M)e modulo-n where M will be one of the 4-digit groups of K0. The leftmost four groups are encrypted as:
An efficient way to compute modular exponentiation is to use the Square-and-Multiply algorithm. This algorithm [21] reduces the number of modular multiplications needed to be performed from e - 1 to at most 2 , where is the number of bits in the binary representation. Let us demonstrate the use of the Square-and-Multiply algorithm by encrypting one of the session-key decimal groups (the eleventh group from the right, M11 = 0032), where n = 2773 and e = 17. In using this algorithm, we first convert e to its binary representation (17 decimal = 10001 binary).
The calculations are illustrated in Table 17.13. Modulo-n math is used, where n = 2773 in this example. The second column contains the binary code, with the most significant bit (MSB) in row 1. Each bit value in this column acts to control a result in column3. The starting value, placed in column 3 row 0, is always 1. Then, the result for any row in column 3 depends on the value of the bit in the corresponding row in column 2; if that entry contains a “1,” then the previous row-result is squared and multiplied by the plaintext (32 for this example). If a row in the second column contains a “0,” then the result of that row in column 3 equals only the square of the previous row’s result. The final value is the encrypted ciphertext (C = 2227). Repeating this method for each of the twelve decimal groups that comprise K0 results in the ciphertext of the session key to be: C = 0000 2227 0000 2704 0753 0001 1278 0272 0001 1405 0272 0001. This RSA-encrypted session key (represented here in decimal) together with the IDEA-encrypted message of 30F9 78B3 E223 E221 (represented here in hex) can now be transmitted over an insecure channel.
Table 17.13 The Square-and-Multiply Algorithm with Plaintext = 32
Row Number |
Binary representation of e (MSB first) |
Modulo multiplication (modulo 2773) |
|---|---|---|
0 |
1 |
|
1 |
1 |
12 × 32 = 32 |
2 |
0 |
322 = 1024 |
3 |
0 |
10242 = 382 |
4 |
0 |
3822 = 1728 |
5 |
1 |
17282 × 32 = 2227 |
17.6.4 PGP Authentication and Signature
The public key algorithms can be used to authenticate or “sign” a message. As illustrated in Figure 17.18, a sender can encrypt a document with his private key (which no one else has access to) prior to encrypting it with the recipient’s public
Equal? If yes, this verifies that the sender is the owner of the public key used and that the message arrived uncorrupted key. The recipient must first use his private key to decrypt the message, followed by a second decryption using the sender’s public key. This technique encrypts the message for secrecy and also provides authentication of the sender.
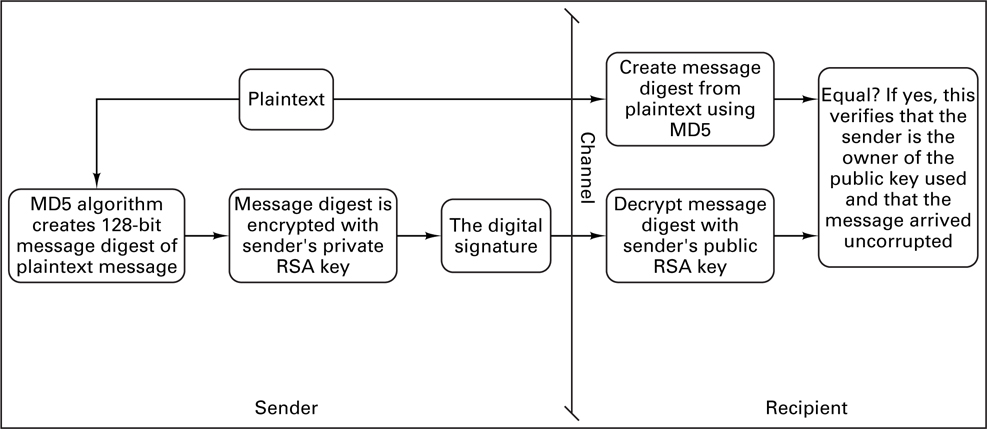
Because of the slowness of public-key algorithms, PGP allows for a different method of authenticating a sender. Instead of the time-consuming process of encrypting the entire plaintext message, the PGP approach encrypts a fixed-length message digest created with a one-way hash function. The encryption of the message digest is performed using a public-key algorithm. This method is known as a digital signature and is shown in Figure 17.22. A digital signature is used to provide authentication of both the sender and the message. Authentication of the message provides a verification that the message was not altered in some way. Using this technique, if a message has been altered in any way (i.e. by a forger), its message digest will be different.
)
){kind=link}
){kind=link}
PGP version 2.6 uses the MD5 (Message Digest 5) algorithm to create a 128-bit message digest (or hash value) of the plaintext. This hash value is then encrypted with the sender’s private key and sent with the plaintext. When the recipient receives the message, he will first decrypt the message digest with the sender’s public key. The recipient will then apply the hash function to the plaintext and compare the two message digests. If they match, the signature is valid. In Figure 17.22, the message is sent without encryption (as plaintext), but it may be encrypted by the method illustrated in Figure 17.20.
17.6.4.1 MD5 and SHA-1
MD5 and SHA-1 are hash functions. A hash function H(x) takes an input and returns a fixed-size string h, called the hash value (also known as a message digest). A cryptographic hash function has the following properties:
The output length is fixed.
The hash value is relatively simple to compute.
The function is one way—in other words, it is hard to invert. If given a hash value h, it is computationally infeasible to find the function’s input x.
The function is collision free. A collision-free hash function is a function for which it is infeasible that two different messages will create the same hash value.
The MD5 algorithm used in PGP version 2.6 creates a 128-bit message digest. The MD5 algorithm processes the text in 512-bit blocks through four rounds of data manipulation. Each round uses a different nonlinear function that consists of the logical operators AND, OR, NOT or XOR. Each function is performed 16 times in a round. Bit shifts and scalar additions are also performed in each round [19]. Hans Dobbertin [18] has determined that collisions may exist in MD5. Because of this potential weakness, the PGP specification recommends using the Digital Signature Standard (DSS). DSS uses the SHA-1 (Secure Hash Algorithm-1) algorithm. The SHA-1 algorithm takes a message of less than 264 bits in length and produces a 160-bit message digest. SHA-1 is similar to MD5 in that it uses a different nonlinear function in each of its 4 rounds. In SHA-1, each function is performed 20 times per round. SHA-1 also uses various scalar additions and bit shifting. The algorithm is slightly slower than MD5 but the larger message digest (160-bit versus 128 bit) makes it more secure against brute-force attacks [19]. A brute-force attack consists of trying many input combinations in an attempt to match the message digest under attack.
17.6.4.2 Digital Signature Standard and RSA
For digital signatures, PGP version 2.6 uses the RSA algorithm for encryption of the hash value produced by the MD5 function; however, versions 5.0 and later adhere to the NIST Digital Signature Standard (DSS) [22]. The NIST DSS requires the use of the SHA-1 hash function. The hash value is then encrypted using the Digital Standard Algorithm (DSA). Like the Diffie-Hellman protocol, DSA is based on the discrete logarithm problem. (Reference [22] contains a detailed description of DSA.)