This chapter is from the book
This chapter is from the book
This chapter is from the book
6.4 Implementing A2C
We now have all of the elements needed to implement the Actor-Critic algorithms. The main components are
Advantage estimation –for example, n-step returns or GAE
Value loss and policy loss
The training loop
In what follows, we discuss an implementation of each of these components, ending with the training loop which brings them all together. Since Actor-Critic conceptually extends REINFORCE, it is implemented by inheriting from the Reinforce class.
Actor-Critic is also an on-policy algorithm since the actor component learns a policy using the policy gradient. Consequently, we train Actor-Critic algorithms using an on-policy Memory, such as OnPolicyReplay which trains in an episodic manner, or OnPolicyBatchReplay which trains using batches of data. The code that follows applies to either approach.
6.4.1 Advantage Estimation
6.4.1.1 Advantage Estimation with n-Step Returns
The main trick when implementing the n-step Qπ estimate is to notice that we have access to the rewards received in an episode in sequence. We can calculate the discounted sum of n rewards for each element of the batch in parallel by taking advantage of vector arithmetic, as shown in Code 6.1. The approach goes as follows:
Initialize a vector rets to populate with the Q-value estimates—that is, n-step returns (line 4).
For efficiency, the computation is done from the last term to the first. The future_ret is a placeholder to accumulate the summed rewards as we work backwards (line 5). It is initialized to next_v_pred since the last term in the n-step Q-estimate is
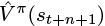.not_dones is a binary variable to handle the episodic boundary and stop the sum from propagating across episodes.
Note that the n-step Q-estimate is defined recursively, that is, Qcurrent = rcurrent + Qnext. This is mirrored exactly by line 8.
Code 6.1 Actor-Critic implementation: calculate n-step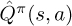 
1 # slm_lab/lib/math_util.py 2 3 def calc_nstep_returns(rewards, dones, next_v_pred, gamma, n): 4 rets = torch.zeros_like(rewards) 5 future_ret = next_v_pred 6 not_dones = 1 - dones 7 for t in reversed(range(n)): 8 rets[t] = future_ret = rewards[t] + gamma * future_ret * not_dones[t] 9 return rets
Now, the ActorCritic class needs a method to compute the advantage estimates and the target V values for computing the policy and value losses, respectively. This is relatively straightforward, as shown in Code 6.2.
One detail about advs and v_targets is important to highlight. They do not have a gradient, as can be seen in the torch.no_grad() and .detach() operations in lines 9–11. In policy loss (Equation 6.1), the advantage only acts as a scalar multiplier to the gradient of the policy log probability. As for the value loss from Algorithm 6.1 (lines 13–14), we assume the target V -value is fixed, and the goal is to train the critic to predict V -value that closely matches it.
Code 6.2 Actor-Critic implementation: calculate n-step advantages and V -target values
1 # slm_lab/agent/algorithm/actor_critic.py
2
3 class ActorCritic(Reinforce):
4 ...
5
6 def calc_nstep_advs_v_targets(self, batch, v_preds):
7 next_states = batch['next_states'][-1]
8 ...
9 with torch.no_grad():
10 next_v_pred = self.calc_v(next_states, use_cache=False)
11 v_preds = v_preds.detach()# adv does not accumulate grad
12 ...
13 nstep_rets = math_util.calc_nstep_returns(batch['rewards'],
↪ batch['dones'], next_v_pred, self.gamma, self.num_step_returns)
14 advs = nstep_rets - v_preds
15 v_targets = nstep_rets
16 ...
17 return advs, v_targets
6.4.1.2 Advantage Estimation with GAE
The implementation of GAE shown in Code 6.3 has a very similar form to that of n-step. It uses the same backward computation, except that we need an extra step to compute the δ term at each time step (line 11).
Code 6.3 Actor-Critic implementation: calculate GAE
1 # slm_lab/lib/math_util.py
2
3 def calc_gaes(rewards, dones, v_preds, gamma, lam):
4 T = len(rewards)
5 assert T + 1 == len(v_preds) # v_preds includes states and 1 last
↪ next_state
6 gaes = torch.zeros_like(rewards)
7 future_gae = torch.tensor(0.0, dtype=rewards.dtype)
8 # to multiply with not_dones to handle episode boundary (last state has no
↪ V(s'))
9 not_dones = 1 - dones
10 for t in reversed(range(T)):
11 delta = rewards[t] + gamma * v_preds[t + 1] * not_dones[t] -
↪ v_preds[t]
12 gaes[t] = future_gae = delta + gamma * lam * not_dones[t] * future_gae
13 return gaes
Likewise, in Code 6.4, the Actor-Critic class method to compute the advantages and target V -values closely follows that of n-step with two important differences. First, calc_gaes (line 14) returns the full advantage estimates, whereas calc_nstep_returns in the n-step case returns Q value estimates. To recover the target V values, we therefore need to add the predicted V -values (line 15). Second, it is good practice to standardize the GAE advantage estimates (line 16).
Code 6.4 Actor-Critic implementation: calculate GAE advantages and V -target values
1 # slm_lab/agent/algorithm/actor_critic.py
2
3 class ActorCritic(Reinforce):
4 ...
5
6 def calc_gae_advs_v_targets(self, batch, v_preds):
7 next_states = batch['next_states'][-1]
8 ...
9 with torch.no_grad():
10 next_v_pred = self.calc_v(next_states, use_cache=False)
11 v_preds = v_preds.detach()# adv does not accumulate grad
12 ...
13 v_preds_all = torch.cat((v_preds, next_v_pred), dim=0)
14 advs = math_util.calc_gaes(batch['rewards'], batch['dones'],
↪ v_preds_all, self.gamma, self.lam)
15 v_targets = advs + v_preds
16 advs = math_util.standardize(advs) # standardize only for advs, not
↪ v_targets
17 ...
18 return advs, v_targets
6.4.2 Calculating Value Loss and Policy Loss
In Code 6.5, the policy loss has the same form as in the REINFORCE implementation. The only difference is that it uses the advantages instead of returns as a reinforcing signal, so we can inherit and reuse the method from REINFORCE (line 7).
The value loss is simply a measure of the error between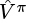 
(v_preds) and 
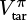(v_targets). We are free to choose any appropriate measure such as MSE by setting the net.loss_spec param in the spec file. This will initialize a loss function self.net_loss_fn used in line 11.
Code 6.5 Actor-Critic implementation: two loss functions
1 # slm_lab/agent/algorithm/actor_critic.py
2
3 class ActorCritic(Reinforce):
4 ...
5
6 def calc_policy_loss(self, batch, pdparams, advs):
7 return super().calc_policy_loss(batch, pdparams, advs)
8
9 def calc_val_loss(self, v_preds, v_targets):
10 assert v_preds.shape == v_targets.shape, f'{v_preds.shape} !=
↪ {v_targets.shape}'
11 val_loss = self.val_loss_coef * self.net.loss_fn(v_preds, v_targets)
12 return val_loss
6.4.3 Actor-Critic Training Loop
The actor and critic can be implemented with either separate networks or a single shared network. This is reflected in the train method in Code 6.6. Lines 10–15 calculate the policy and value losses for training. If the implementation uses a shared network (line 16), the two losses are combined and used to train the network (lines 17–18). If the actor and critic are separate networks, the two losses are used separately to train the relevant networks (lines 20–21). Section 6.5 goes into more details on network architecture.
Code 6.6 Actor-Critic implementation: training method
1 # slm_lab/agent/algorithm/actor_critic.py
2
3 class ActorCritic(Reinforce):
4 ...
5
6 def train(self):
7 ...
8 clock = self.body.env.clock
9 if self.to_train == 1:
10 batch = self.sample()
11 clock.set_batch_size(len(batch))
12 pdparams, v_preds = self.calc_pdparam_v(batch)
13 advs, v_targets = self.calc_advs_v_targets(batch, v_preds)
14 policy_loss = self.calc_policy_loss(batch, pdparams, advs)# from
↪ actor
15 val_loss = self.calc_val_loss(v_preds, v_targets)# from critic
16 if self.shared:# shared network
17 loss = policy_loss + val_loss
18 self.net.train_step(loss, self.optim, self.lr_scheduler,
↪ clock=clock, global_net=self.global_net)
19 else:
20 self.net.train_step(policy_loss, self.optim,
↪ self.lr_scheduler, clock=clock,
↪ global_net=self.global_net)
21 self.critic_net.train_step(val_loss, self.critic_optim,
↪ self.critic_lr_scheduler, clock=clock,
↪ global_net=self.global_critic_net)
22 loss = policy_loss + val_loss
23 # reset
24 self.to_train = 0
25 return loss.item()
26 else:
27 return np.nan