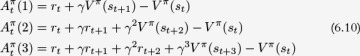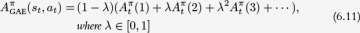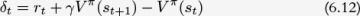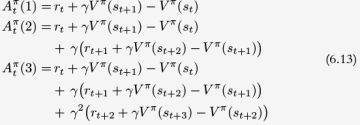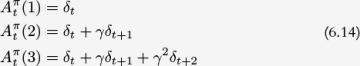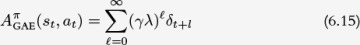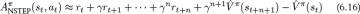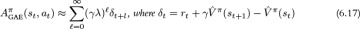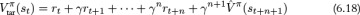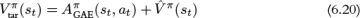6.2 The Critic
Critics are responsible for learning how to evaluate (s, a) pairs and using this to generate Aπ.
In what follows, we first describe the advantage function and why it is a good choice for a reinforcing signal. Then, we present two methods for estimating the advantage function—n-step returns and Generalized Advantage Estimation [123]. Finally, we discuss how they can be learned in practice.
6.2.1 The Advantage Function
Intuitively, the advantage function Aπ(st, at) measures the extent to which an action is better or worse than the policy’s average action in a particular state. The advantage is defined in Equation 6.3.
It has a number of nice properties. First, 𝔼a∈𝒜[Aπ(st, a)] = 0. This implies that if all actions are essentially equivalent, then Aπ will be 0 for all actions and the probability of taking these actions will remain unchanged when the policy is trained using Aπ. Compare this to a reinforcing signal based on absolute state or state-action values. This signal would have a constant value in the same situation, but it may not be 0. Consequently, it would actively encourage (if positive) or discourage (if negative) the action taken. Since all actions were equivalent, this may not be problematic in practice, although it is unintuitive.
A more problematic example is if the action taken was worse than the average action, but the expected return is still positive. That is, Qπ(st, at) > 0, but Aπ(st, at) < 0. Ideally, the action taken should become less likely since there were better options available. In this case using Aπ yields behavior which matches our intuition more closely since it will discourage the action taken. Using Qπ, or even Qπ with a baseline, may encourage the action.
The advantage is also a relative measure. For a particular state s and action a, it considers the value of the state-action pair, Qπ(s, a), and evaluates whether a will take the policy to a better or worse place, measured relative to Vπ(s). The advantage avoids penalizing an action for the policy currently being in a particularly bad state. Conversely, it does not give credit to an action for the policy being in a good state. This is beneficial because a can only affect the future trajectory, but not how a policy arrived in the current state. We should evaluate the action based on how it changes the value in the future.
Let’s look at an example. In Equation 6.4, the policy is in a good state with Vπ(s) = 100, whereas in Equation 6.5, it is in a bad state with Vπ(s) = −100. In both cases, action a yields a relative improvement of 10, which is captured by each case having the same advantage. However, this would not be clear if we looked at just Qπ(s, a).
Understood this way, the advantage function is able to capture the long-term effects of an action, because it considers all future time steps,1 while ignoring the effects of all the actions to date. Schulman et al. present a similar interpretation in their paper “Generalized Advantage Estimation” [123].
Having seen why the advantage function Aπ(s, a) is a good choice of reinforcing signal to use in an Actor-Critic algorithm, let’s look at two ways of estimating it.
6.2.1.1 Estimating Advantage: n-Step Returns
To calculate the advantage Aπ, we need an estimate for Qπ and Vπ. One idea is that we could learn Qπ and Vπ separately with different neural networks. However, this has two disadvantages. First, care needs to be taken to ensure the two estimates are consistent. Second, it is less efficient to learn. Instead, we typically learn just Vπ and combine it with rewards from a trajectory to estimate Qπ.
Learning Vπ is preferred to learning Qπ for two reasons. First, Qπ is a more complex function and may require more samples to learn a good estimate. This can be particularly problematic in the setting where the actor and the critic are trained jointly. Second, it can be more computationally expensive to estimate Vπ from Qπ. Estimating Vπ(s) from Qπ(s, a) requires computing the values for all possible actions in state s, then taking the action-probability weighted average to obtain Vπ(s). Additionally, this is difficult for environments with continuous actions since estimating Vπ would require a representative sample of actions from a continuous space.
Let’s look at how to estimate Qπ from Vπ.
If we assume for a moment that we have a perfect estimate of Vπ(s), then the Q-function can be rewritten as a mix of the expected rewards for n time steps, followed by Vπ(sn+1) as shown in Equation 6.6. To make this tractable to estimate, we use a single trajectory of rewards (r1, . . . , rn) in place of the expectation, and substitute in  learned by the critic. Shown in Equation 6.7, this is known as n-step forward returns.
learned by the critic. Shown in Equation 6.7, this is known as n-step forward returns.
Equation 6.7 makes the tradeoff between bias and variance of the estimator explicit. The n steps of actual rewards are unbiased but have high variance since they come from only a single trajectory.  has lower variance since it reflects an expectation over all of the trajectories seen so far, but is biased because it is calculated using a function approximator. The intuition behind mixing these two types of estimates is that the variance of the actual rewards typically increases the more steps away from t you take. Close to t, the benefits of using an unbiased estimate may outweigh the variance introduced. As n increases, the variance in the estimates will likely start to become problematic, and switching to a lower-variance but biased estimate is better. The number of steps of actual rewards, n, controls the tradeoff between the two.
has lower variance since it reflects an expectation over all of the trajectories seen so far, but is biased because it is calculated using a function approximator. The intuition behind mixing these two types of estimates is that the variance of the actual rewards typically increases the more steps away from t you take. Close to t, the benefits of using an unbiased estimate may outweigh the variance introduced. As n increases, the variance in the estimates will likely start to become problematic, and switching to a lower-variance but biased estimate is better. The number of steps of actual rewards, n, controls the tradeoff between the two.
Combining the n-step estimate for Qπ with 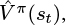 we get an formula for estimating the advantage function, shown in Equation 6.8.
we get an formula for estimating the advantage function, shown in Equation 6.8.
The number of steps of actual rewards, n, controls the amount of variance in the advantage estimator, and is a hyperparameter that needs to be tuned. Small n results in an estimator with lower variance but higher bias, large n results in an estimator with higher variance but lower bias.
6.2.1.2 Estimating Advantage: Generalized Advantage Estimation (GAE)
Generalized Advantage Estimation (GAE) [123] was proposed by Schulman et al. as an improvement over the n-step returns estimate for the advantage function. It addresses the problem of having to explicitly choose the number of steps of returns, n. The main idea behind GAE is that instead of picking one value of n, we mix multiple values of n. That is, we calculate the advantage using a weighted average of individual advantages calculated with n = 1, 2, 3, . . . , k. The purpose of GAE is to significantly reduce the variance of the estimator while keeping the bias introduced as low as possible.
GAE is defined as an exponentially weighted average of all of the n-step forward return advantages. It is shown in Equation 6.9 and the full derivation for GAE is given in Box 6.1.
Intuitively, GAE is taking a weighted average of a number of advantage estimators with different bias and variance. GAE weights the high-bias, low-variance 1-step advantage the most, but also includes contributions from lower-bias, higher-variance estimators using 2, 3, . . . , n steps. The contribution decays at an exponential rate as the number of steps increases. The decay rate is controlled by the coefficient λ. Therefore, the larger λ, the higher the variance.
Box 6.1 Generalized Advantage Estimation Derivation
Both GAE and the n-step advantage function estimates include the discount factor γ which controls how much an algorithm “cares” about future rewards compared to the current reward. Additionally, they both have a parameter that controls the bias-variance tradeoff: n for the advantage function and λ for GAE. So what have we gained with GAE?
Even though n and λ both control the bias-variance tradeoff, they do so in different ways. n represents a hard choice, since it precisely determines the point at which the high-variance rewards are switched for the V -function estimate. In contrast, λ represents a soft choice: smaller values of λ will more heavily weight the V -function estimate, whilst larger values will weight the actual rewards more. However, unless λ = 02 or λ = 1,3 using λ still allows higher or lower variance estimates to contribute—hence the soft choice.
6.2.2 Learning the Advantage Function
We have seen two ways to estimate the advantage function. Both these methods assume we have access to an estimate for Vπ, as shown below.
We learn Vπ using TD learning in the same way we used it to learn Qπ for DQN. In brief, learning proceeds as follows. Parametrize Vπ with θ, generate 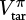 for each of the experiences an agent gathers, and minimize the difference between
for each of the experiences an agent gathers, and minimize the difference between 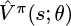 and
and 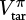 using a regression loss such as MSE. Repeat this process for many steps.
using a regression loss such as MSE. Repeat this process for many steps.
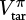 can be generated using any appropriate estimate. The simplest method is to set
can be generated using any appropriate estimate. The simplest method is to set  . This naturally generalizes to an n-step estimate, as shown in Equation 6.18.
. This naturally generalizes to an n-step estimate, as shown in Equation 6.18.
Alternatively, we can use a Monte Carlo estimate for  shown in Equation 6.19.
shown in Equation 6.19.
Or, we can set
Practically, to avoid additional computation, the choice of  is often related to the method used to estimate the advantage. For example, we can use Equation 6.18 when estimating advantages using n-step returns, or Equation 6.20 when estimating advantages using GAE.
is often related to the method used to estimate the advantage. For example, we can use Equation 6.18 when estimating advantages using n-step returns, or Equation 6.20 when estimating advantages using GAE.
It is also possible to use a more advanced optimization procedure when learning 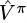 is learned using a trust-region method.
is learned using a trust-region method.
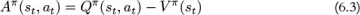

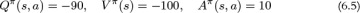
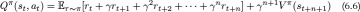
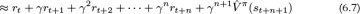
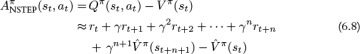
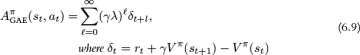
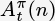 is used to denote the advantage estimator calculated with n-step forward returns. For example, Equation 6.10 shows
is used to denote the advantage estimator calculated with n-step forward returns. For example, Equation 6.10 shows 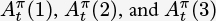 .
.