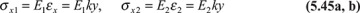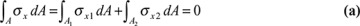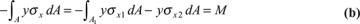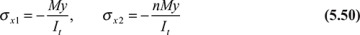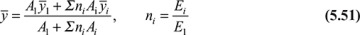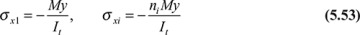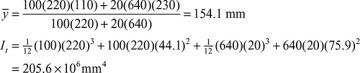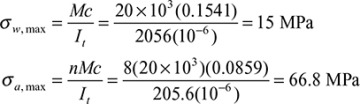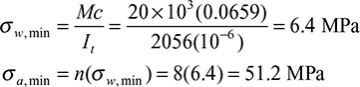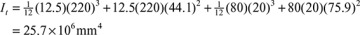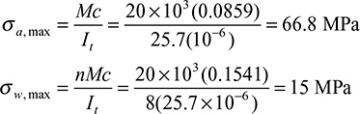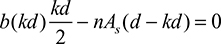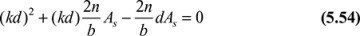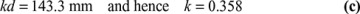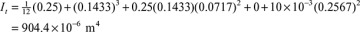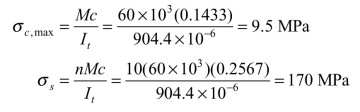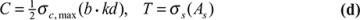- 5.1 Introduction
- 5.2 Pure Bending of Beams of Symmetrical Cross Section
- 5.3 Pure Bending of Beams of Asymmetrical Cross Section
- 5.4 Bending of A Cantilever of Narrow Section
- 5.5 Bending of a Simply Supported Narrow Beam
- 5.6 Elementary Theory of Bending
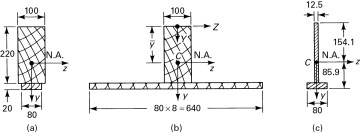
- 5.7 Normal and Shear Stresses
- 5.8 Effect of Transverse Normal Stress
- 5.9 Composite Beams
- 5.10 Shear Center
- 5.11 Statically Indeterminate Systems
- 5.12 Energy Method for Deflections
- 5.13 Elasticity Theory
- 5.14 Curved Beam Formula
- 5.15 Comparison of the Results of Various Theories
- 5.16 Combined Tangential and Normal Stresses
- References
- Problems
This chapter is from the book
This chapter is from the book
This chapter is from the book
5.9 Composite Beams
Beams constructed of two or more materials having different moduli of elasticity are referred to as composite beams. Examples include multilayer beams made by bonding together multiple sheets, sandwich beams consisting of high-strength material faces separated by a relatively thick layer of low-strength material such as plastic foam, and reinforced concrete beams. The assumptions of the technical theory for a homogeneous beam (Section 5.6) are valid for a beam composed of more than one material.
5.9.1 Transformed Section Method
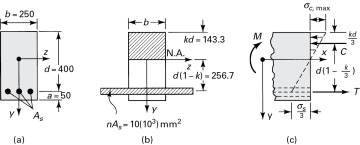
To analyze composite beams, we will use the common transformed-section method. In this technique, the cross sections of several materials are transformed into an equivalent cross section of one material on which the resisting forces and the neutral axis are the same as on the original section. The usual flexure formula is then applied to the new section. To illustrate this method, we will use a frequently encountered example: a beam with a symmetrical cross section built of two different materials (Fig. 5.15a).
)
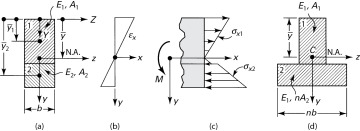
Figure 5.15. Beam composed of two materials: (a) composite cross section; (b) strain distribution; (d) transformed cross section.
The cross sections of the beam remain plane during bending. Hence, the condition of geometric compatibility of deformation is satisfied. It follows that the normal strain ɛx varies linearly with the distance y from the neutral axis of the section; that is, ɛx = ky (Figs. 5.15a and b). The location of the neutral axis is yet to be determined. Both materials composing the beam are assumed to obey Hooke′s law, and their moduli of elasticity are designated as E1 and E2. Then, the stress—strain relation gives
)
This result is sketched in Fig. 5.13c for the assumption that E2 > E1. We introduce the notation
)
where n is called the modular ratio. Note that n >1 in Eq. (5.46). However, this choice is arbitrary; the technique applies as well for n > 1.
5.9.2 Equation of Neutral Axis
Referring to the cross section (Figs. 5.15a and c), the equilibrium equations ΣFx = 0 and ΣMz = 0 lead to
)
)
where A1 and A2 denote the cross-sectional areas for materials 1 and 2, respectively. Substituting σx1, σx2 and n, as given by Eqs. (5.45) and (5.46), into Eq. (a) results in
)
Using the top of the section as a reference (Fig. 5.15a), from Eq. (5.47) with
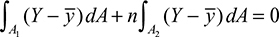
or, setting
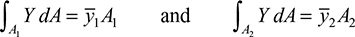
we have
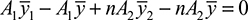
This expression yields an alternative form of Eq. (5.47):
)
Equations (5.47) and (5.47') can be used to locate the neutral axis for a beam of two materials. These equations show that the transformed section will have the same neutral axis as the original beam, provided the width of area 2 is changed by a factor n and area 1 remains the same (Fig. 5.15d). Clearly, this widening must be effected in a direction parallel to the neutral axis, since the distance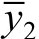 
to the centroid of area 2 remains unchanged. The new section constructed in this way represents the cross section of a beam made of a homogeneous material with a modulus of elasticity E1 and with a neutral axis that passes through its centroid, as shown in Fig. 5.15d.
5.9.3 Stresses in the Transformed Beam
Similarly, condition (b) together with Eqs. (5.45) and (5.46) leads to
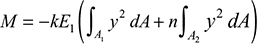
or
)
where I1 and I2 are the moments of inertia about the neutral axis of the cross-sectional areas 1 and 2, respectively. Note that
)
is the moment of inertia of the entire transformed area about the neutral axis. From Eq. (5.48), we have
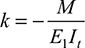
The flexure formulas for a composite beam are obtained by introducing this relation into Eqs. (5.45):
)
where σx1 and σx2 are the stresses in materials 1 and 2, respectively. Note that when E1 = E2 = E, Eqs. (5.50) reduce to the flexure formula for a beam of homogeneous material, as expected.
5.9.4 Composite Beams of Multi Materials
The preceding discussion may be extended to include composite beams consisting of more than two materials. It is readily shown that for m different materials, Eqs. (5.47′), (5.49), and (5.50) take the forms
)
)
)
where i = 2, 3,..., m denotes the ith material.
The use of the formulas developed in this section is demonstrated in the solutions of the numerical problems in Examples 5.7 and 5.8.
EXAMPLE 5.7 ALUMINUM-REINFORCED WOOD BEAM
A wood beam with Ew = 8.75 GPa, 100 mm wide by 220 mm deep, has an aluminum plate Ea = 70 GPa with a net section 80 mm by 20 mm securely fastened to its bottom face, as shown in Fig. 5.16a. Dimensions are given in millimeters. The beam is subjected to a bending moment of 20 kN·m around a horizontal axis. Calculate the maximum stresses in both materials (a) using a transformed section of wood and (b) using a transformed section of aluminum.
)
Figure 5.16. Example 5.7. (a) Composite cross section; (b) equivalent wood cross section; (c) equivalent aluminum cross section.
Solution
The modular ratio is n = Ea/Ew = 8. The centroid and the moment of inertia about the neutral axis of the transformed section (Fig. 5.16b) are
In turn, the maximum stresses in the wood and aluminum portions are
At the juncture of the two parts,
For this case, the modular ratio is n = Ew/Ea = 1/8 and the transformed area is shown in Fig. 5.16c. We now have
)
)
)
)
Then
)
as have already been found in part (a).
EXAMPLE 5.8 STEEL-REINFORCED-CONCRETE BEAM
A concrete beam of width b = 250 mm and effective depth d = 400 mm is reinforced with three steel bars, providing a total cross-sectional area As = 1000 mm2 (Fig. 5.17a). Dimensions are given in millimeters. Note that it is usual for an approximate allowance a = 50 mm to be used to protect the steel from corrosion and fire. Let n = Es/Ec = 10. Calculate the maximum stresses in the materials produced by a negative bending moment of M = 60 kN·m.
Solution Concrete is very weak in tension but strong in compression. Thus, only the portion of the cross section located a distance kd above the neutral axis is used in the transformed section (Fig. 5.17b); the concrete is assumed to take no tension. The transformed area of the steel nAs is identified by a single dimension from the neutral axis to its centroid. The compressive stress in the concrete is assumed to vary linearly from the neutral axis, and the steel is assumed to be uniformly stressed.
)
Figure 5.17. Example 5.8. (a) Reinforced-concrete cross section; (b) equivalent concrete cross section; (c) compressive force C in concrete and tensile force T in the steel rods.
The condition that the first moment of the transformed section with respect to the neutral axis be zero is satisfied by
or
)
By solving this quadratic expression for kd, we can obtain the position of the neutral axis.
Introducing the data given, Eq. (5.54) reduces to
from which
)
The moment of inertia of the transformed cross section about the neutral axis is
)
Thus, the peak compressive stress in the concrete and the tensile stress in the steel are
)
These stresses act as shown in Fig. 5.15c.
An alternative method of solution is to obtain σc,max and σs from a free-body diagram of the portion of the beam (Fig. 5.17c) without computing It. The first equilibrium condition, ΣFx = 0, gives C = T where
)
are the compressive and tensile stress resultants, respectively. From the second requirement of statics, ΣMz = 0, we have
)
Equations (d) and (e) result in
)
Substituting the data given and Eq. (c) into Eq. (5.55) yields
)
){kind=link}
as before.