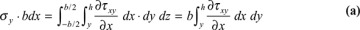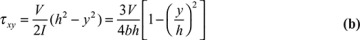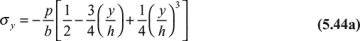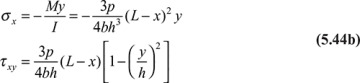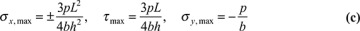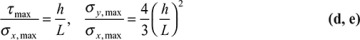- 5.1 Introduction
- 5.2 Pure Bending of Beams of Symmetrical Cross Section
- 5.3 Pure Bending of Beams of Asymmetrical Cross Section
- 5.4 Bending of A Cantilever of Narrow Section
- 5.5 Bending of a Simply Supported Narrow Beam
- 5.6 Elementary Theory of Bending
- 5.7 Normal and Shear Stresses
- 5.8 Effect of Transverse Normal Stress
- 5.9 Composite Beams
- 5.10 Shear Center
- 5.11 Statically Indeterminate Systems
- 5.12 Energy Method for Deflections
- 5.13 Elasticity Theory
- 5.14 Curved Beam Formula
- 5.15 Comparison of the Results of Various Theories
- 5.16 Combined Tangential and Normal Stresses
- References
- Problems
This chapter is from the book
This chapter is from the book
This chapter is from the book
5.8 Effect of Transverse Normal Stress
When a beam is subjected to a transverse load, a transverse normal stress is created. According to Eq. (5.26), this stress is not related to the normal strain εy, so it cannot be determined using Hooke′s law. However, an expression for the average transverse normal stress can be obtained from the equilibrium requirement of force balance along the axis of the beam. For this purpose, a procedure is used similar to that employed for determining the shear stress in Section 5.7.
Consider, for example, a rectangular cantilever beam of width b and depth 2h subject to a uniform load of intensity p (Fig. 5.14a). The free-body diagram of an isolated beam segment of length dx is shown in Fig. 5.14b. Passing a horizontal plane through this segment results in the free-body diagram of Fig. 5.14c, for which the condition of statics ΣFy = 0 yields
)
)
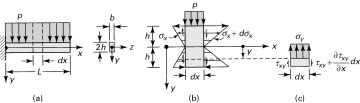
Figure 5.14. (a) Uniformly loaded cantilever beam of rectangular cross section; (b) free-body diagram of a segment; (c) stresses in a beam element.
Here, the shear stress is defined by Eq. (5.41) as
)
After substituting Eqs. (5.28) and (b) into Eq. (a), we have
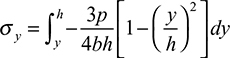
Integration yields the transverse normal stress in the form
)
This stress varies as a cubic parabola, ranging from −plb at the surface (y = −h) where the load acts, to zero at the opposite surface (y = h).
The distribution of the bending and the shear stresses in a uniformly loaded cantilever beam (Fig. 5.12a) is determined from Eqs. (5.38) and (b):
)
The largest values of σx, τxy, and σy given by Eqs. (5.44) are
)
To compare the magnitudes of the maximum stresses, consider the following ratios:
)
){kind=link}
Because L is much greater than h in most beams (L ≥ 20h), the shear and the transverse normal stresses will usually be orders of magnitude smaller than the bending stresses. This justification is the rationale for assuming γxy = 0 and ɛy = 0 in the technical theory of bending. Note that Eq. (e) results in even smaller values than Eq. (d). Therefore, in practice, it is reasonable to neglect σy.
The foregoing conclusion applies, in most cases, to beams of a variety of cross-sectional shapes and under various load configurations. Clearly, the factor of proportionality in Eqs. (d) and (e) will differ for beams of different sectional forms and for different loadings of a given beam.