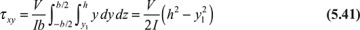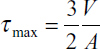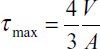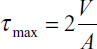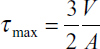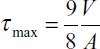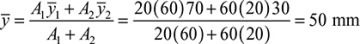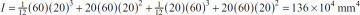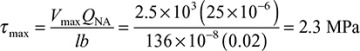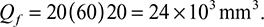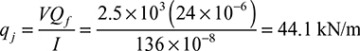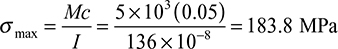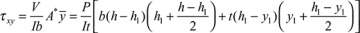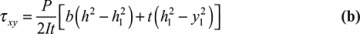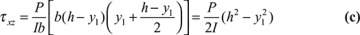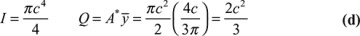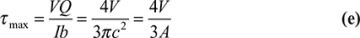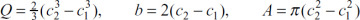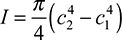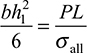- 5.1 Introduction
- 5.2 Pure Bending of Beams of Symmetrical Cross Section
- 5.3 Pure Bending of Beams of Asymmetrical Cross Section
- 5.4 Bending of A Cantilever of Narrow Section
- 5.5 Bending of a Simply Supported Narrow Beam
- 5.6 Elementary Theory of Bending
- 5.7 Normal and Shear Stresses
- 5.8 Effect of Transverse Normal Stress
- 5.9 Composite Beams
- 5.10 Shear Center
- 5.11 Statically Indeterminate Systems
- 5.12 Energy Method for Deflections
- 5.13 Elasticity Theory
- 5.14 Curved Beam Formula
- 5.15 Comparison of the Results of Various Theories
- 5.16 Combined Tangential and Normal Stresses
- References
- Problems
This chapter is from the book
This chapter is from the book
This chapter is from the book
5.7 Normal and Shear Stresses
When a beam is bent by transverse loads, usually both a bending moment M and a shear force V act on each cross section. The distribution of the normal stress associated with the bending moment is given by the flexure formula, Eq. (5.4):
)
where M and I are taken with respect to the z axis (Fig. 5.7).
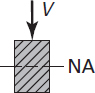
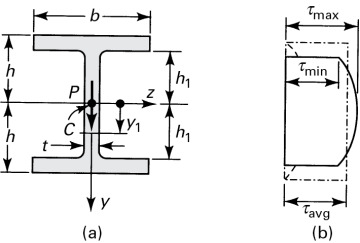
In accordance with the assumptions of elementary bending, Eqs. (5.26) and (5.27), we omit the contribution of the shear strains to beam deformation in these calculations. However, shear stresses do exist, and the shearing forces are the resultant of the stresses. The shearing stress τxy acting at section mn, which is assumed to be uniformly distributed over the area b·dx, can be determined on the basis of equilibrium of forces acting on the shaded part of the beam element (Fig. 5.9). Here b is the width of the beam a distance y1 from the neutral axis, and dx is the length of the element. The distribution of normal stresses produced by M and M + dM is indicated in the figure. The normal force distributed over the left face mr on the shaded area A* is equal to
)
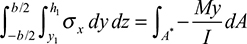
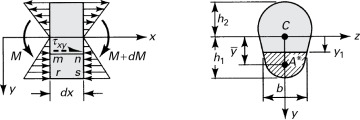
Figure 5.9. (a) Beam segment for analyzing shear stress; (b) cross section of beam.
Similarly, an expression for the normal force on the right face ns may be written in terms of M + dM. The equilibrium of x-directed forces acting on the beam element is governed by
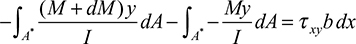
from which we have
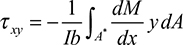
After substituting in Eq. (5.29), we obtain the shear formula (also called the shear stress formula) for beams:
)
The integral represented by Q is the first moment of the shaded area A* with respect to the neutral axis z:
)
By definition,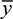 
is the distance from the neutral axis to the centroid of A*. In the case of sections of regular geometry, 
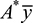provides a convenient means of calculating Q. The shear force acting across the width of the beam per unit length
)
is called the shear flow.
5.7.1 Rectangular Cross Section
In the case of a rectangular cross section of width b and depth 2h, the shear stress at y1 is
)
This equation shows that the shear stress varies parabolically with y1. It is zero when y1 = ±h, and has its maximum value at the neutral axis:
)
where A = 2bh is the area of the rectangular cross section. Note that the maximum shear stress (either horizontal or vertical: τxy = τyx) is 1.5 times larger than the average shear stress V/A. As observed in Section 5.4, for a thin rectangular beam, Eq. (5.42) is the exact distribution of shear stress. More generally, for wide rectangular sections and for other sections, Eq. (5.39) yields only approximate values of the shearing stress.
5.7.2 Various Cross Sections
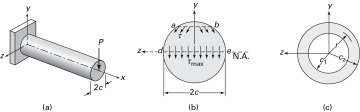
Because the shear formula for beams is based on the flexure formula, the limitations of the bending formula apply when it is used. Problems involving various types of cross sections can be solved by following procedures identical to that for rectangular sections. Table 5.1 shows some typical cases. Observe that shear stress can always be expressed as a constant times the average shear stress (P/A), where the constant is a function of the cross-sectional form. Nevertheless, the maximum shear stress does not always occur at the neutral axis. For instance, in the case of a cross section having nonparallel sides, such as a triangular section, the maximum value of Q/b (and thus τxy) occurs at midheight, h/2, while the neutral axis is located at a distance h/3 from the base.
Table 5.1. Maximum Shearing Stress for Some Typical Beam Cross-Sectional Forms
Cross Section |
Maximum Shearing Stress |
Location |
|
|---|---|---|---|
Rectangle |
|
|
NA |
Circle |
|
|
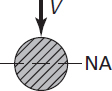
NA |
Hollow Circle |
|
|
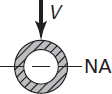
NA |
Triangle |
|
|
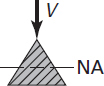
Halfway between top and bottom |
Diamond |
|
|
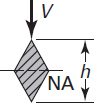
At h/8 above and below the NA |
Notes: A, cross-sectional area; V, transverse shear force; NA, the neutral axis.
The following examples illustrate the application of the normal and shear stress formulas.
EXAMPLE 5.3 STRESSES IN A BEAM OF T-SHAPED CROSS SECTION
A simply supported beam of length L carries a concentrated load P (Fig. 5.10a). Find: (a) The maximum shear stress, the shear flow qj, and the shear stress Tj in the joint between the flange and the web; (b) the maximum bending stress. Given: P = 5 kN and L = 4 m.
)
Figure 5.10. Example 5.3. (a) Load diagram and beam cross section; (b) shear diagram; (c) moment diagram.
Solution The distance from the Z axis to the centroid is obtained as follows (Fig. 5.10a):
)
The moment of inertia I about the NA is determined by the parallel axis theorem:
)
The shear and moment diagrams (Figs. 5.10b and c) are sketched by applying the method of sections.
The maximum shearing stress in the beam takes place at the NA on the cross section supporting the largest shear force V. Consequently, QNA = 50(20)25 = 25×103 mm3. The shear force equals 2.5 kN on all cross sections of the beam (Fig. 5.10b), Thus,
The first moment of the area of the flange about the NA is
Shear flow and shear stress in the joint are
and τj = qj/b = 44.1/0.02 = 2.205 MPa.
The largest moment takes place at midspan (Fig. 5.10c). Equation (5.39) is therefore
)
)
EXAMPLE 5.4 SHEAR STRESSES IN A FLANGED BEAM
A cantilever wide-flange beam is loaded by a force P at the free end acting through the centroid of the section. The beam is of constant thickness t (Fig. 5.11a). Determine the shear stress distribution in the section.
)
Figure 5.11. Example 5.4. (a) Cross section of a wide-flange beam; (b) shearing stress distribution.
Solution The vertical shear force at every section is P. It is assumed that the shear stress τxy is uniformly distributed over the web thickness. Then, in the web, for 0 ≤ y1 ≤ h1 and applying Eq. (5.39),
)
This equation may be written as
)
The shearing stress thus varies parabolically in the web (Fig. 5.11b). The extreme values of τxy found at y1 = 0 and y1 = ± h1 are, from Eq. (b), as follows:
)
Usually t≫b so that the maximum and minimum stresses do not differ appreciably, as is seen in the figure. Similarly, the shear stress in the flange, for h1 < y1 ≤ h, is
)
This is the parabolic equation for the variation of stress in the flange, shown by the dashed lines in Fig. 5.11b.
Comments Clearly, for a thin flange, the shear stress is very small as compared with the shear stress in the web. As a consequence, the approximate average value of shear stress in the beam may be found by dividing P by the web cross section, with the web height assumed to be equal to the beam′s overall height: τavg = p/2. This result is indicated by the dotted lines in Fig. 5.11b.
The distribution of stress given by Eq. (c) is fictitious, because the inner planes of the flanges must be free of shearing stress, as they are load-free boundaries of the beam. This contradiction cannot be resolved by the elementary theory; instead, the theory of elasticity must be applied to obtain the correct solution. Fortunately, this defect of the shearing stress formula does not lead to serious error since, as pointed out previously, the web carries almost all the shear force. To reduce the stress concentration at the juncture of the web and the flange, the sharp corners should be rounded.
EXAMPLE 5.5 BEAM OF CIRCULAR CROSS SECTION
A cantilever beam of circular cross section supports a concentrated load P at its free end (Fig. 5.12a). The shear force V in this beam is constant and equal to the magnitude of the load P = V. Find the maximum shearing stresses (a) in a solid cross section and (b) in a hollow cross section.
)
Figure 5.12. Example 5.5. (a) A cantilever beam under a load P; (b) shear stress distribution on a circular cross section; (c) hollow circular cross section.
Assumptions: All shear stresses do not act parallel to the y axis. At a point such as a or b on the boundary of the cross section, the shear stress τ must act parallel to the boundary. The shear stresses at line ab across the cross section are not parallel to the y axis and cannot be determined by the shear formula, τ = VQ/Ib. The maximum shear stresses occur along the neutral axis z, are uniformly distributed, and act parallel to the y axis. These stresses are within approximately 5% of their true value [Ref. 5.1].
Solution
Solid Cross Section (Fig. 5.12b). The shear formula may be used to calculate, with reasonable accuracy, the shear stresses at the neutral axis. The area properties for a circular cross section of radius c (see Table C.1) are
and b = 2c. The maximum shear stress is thus
where A is the cross-sectional area of the beam.
Comment This result shows that the largest shear stress in a circular beam is 4/3 times the average shear stress τavg = V/A.
Hollow Circular Cross Section (Fig. 5.11c). Equation (5.43) applies with equal rigor to circular tubes, since the same assumptions stated in the foregoing are valid. But in this case, by Eq. (C.3), we have
)
)
)
and
So, the maximum shear stress may be written in the following form:
)
Comment Note that for c1 = 0, Eq. (e) reduces to Eq. (5.43) for a solid circular beam, as expected. In the special case of a thin-walled tube, we have r/t > 10, where r and t represent the mean radius and thickness, respectively. As a theoretical limiting case, setting c2 = c1 = r means that Eq. (e) results in τmax = 2V/A.
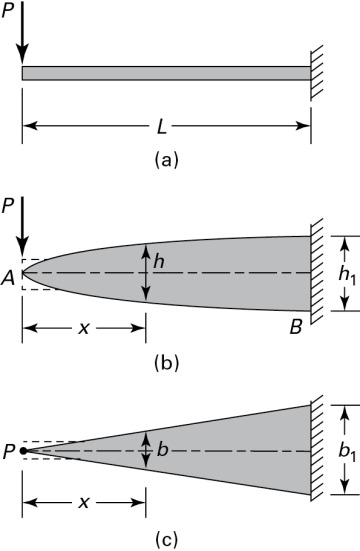
5.7.3 Beam of Constant Strength
When a beam is stressed to a constant permissible stress, σall throughout, then clearly the beam material is used to its greatest capacity. For a given material, such a design is of minimum weight. At any cross section, the required section modulus S is defined as
)
where M presents the bending moment on an arbitrary section. Tapered beams designed in this way are called beams of constant strength. Ultimately, the shear stress at those beam locations where the moment is small controls the design.
Examples of beams with uniform strength include leaf springs and certain cast machine elements. For a structural member, fabrication and design constraints make it impractical to produce a beam of constant stress. Hence, welded cover plates are often used for parts of prismatic beams where the moment is large—for instance, in a bridge girder. When the angle between the sides of a tapered beam is small, the flexure formula allows for little error. On the contrary, the results found by applying the shear stress formula may not be accurate enough for nonprismatic beams. Often, a modified form of this formula is used for design purposes. The exact distribution in a rectangular wedge is found by applying the theory of elasticity (Section 3.10).
EXAMPLE 5.6 DESIGN OF A UNIFORM STRENGTH BEAM
A cantilever beam of constant strength and rectangular cross section is to carry a concentrated load P at the free end (Fig. 5.13a). Find the required cross-sectional area for two cases: (a) the width b is constant; (b) the height h is constant.
)
Figure 5.13. Example 5.6. (a) Constantstrength cantilever; (b) side view; (c) top view.
Solution
At a distance x from A, M = Px and S = bh2/6. By applying Eq. (5.43), we have
Likewise, at a fixed end (x = L and h = h1),
Dividing Eq. (g) by the preceding relationship leads to
Thus, the depth of the beam varies parabolically from the free end (Fig. 5.13b).
Equation (g) now gives
)
)
)
){kind=link}
Comments In Eq. (i), the term in parentheses represents a constant and is set equal to b1/L; hence, when x = L, the width is b1 (Fig. 5.13c). Clearly, the cross section of the beam near end A must be designed to resist the shear force, as depicted by the dashed lines in the figure.