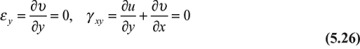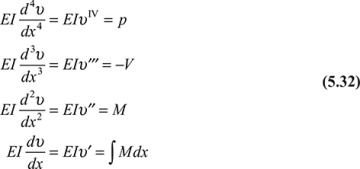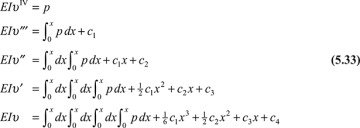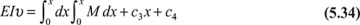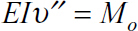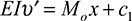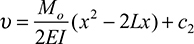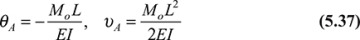- 5.1 Introduction
- 5.2 Pure Bending of Beams of Symmetrical Cross Section
- 5.3 Pure Bending of Beams of Asymmetrical Cross Section
- 5.4 Bending of A Cantilever of Narrow Section
- 5.5 Bending of a Simply Supported Narrow Beam
- 5.6 Elementary Theory of Bending
- 5.7 Normal and Shear Stresses
- 5.8 Effect of Transverse Normal Stress
- 5.9 Composite Beams
- 5.10 Shear Center
- 5.11 Statically Indeterminate Systems
- 5.12 Energy Method for Deflections
- 5.13 Elasticity Theory
- 5.14 Curved Beam Formula
- 5.15 Comparison of the Results of Various Theories
- 5.16 Combined Tangential and Normal Stresses
- References
- Problems
This chapter is from the book
This chapter is from the book
This chapter is from the book
5.6 Elementary Theory of Bending
We may conclude, on the basis of the previous sections, that exact solutions are difficult to obtain. We also observed that for a slender beam, the results of the exact theory do not differ markedly from those found with the mechanics of materials or elementary approach provided that solutions close to the ends are not required. The bending deflection is very much larger than the shear deflection, so the stress associated with the former predominates. As a consequence, the normal strain εy resulting from transverse loading may be neglected.
Because it is more easily applied, the elementary approach is usually preferred in engineering practice. The exact and elementary theories should be regarded as complementary—rather than competitive—approaches, enabling the analyst to obtain the degree of accuracy required in the context of the specific problem at hand.
5.6.1 Assumptions of Elementary Theory
The basic presuppositions of the elementary theory [Ref. 5.2], for a slender beam whose cross section is symmetrical about the vertical plane of loading, are
)
)
)
The first equation of Eqs. (5.26) is equivalent to the assertion υ = υ(x). Thus, all points in a beam at a given longitudinal location x experience identical deformation. The second equation of Eqs. (5.26), together with υ = υ(x), yields, after integration,
)
The third equation of Eqs. (5.26) and Eqs. (5.27) imply that the beam is considered narrow, and we have a case of plane stress.
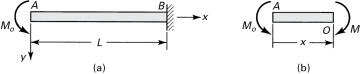
At y = 0 the bending deformation should vanish. Referring to Eq. (a), it is clear that u0(x) must represent axial deformation. The term dυ/dx is the slope θ of the beam axis, as shown in Fig. 5.7a, and is very much smaller than unity. Therefore,
)
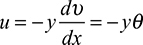
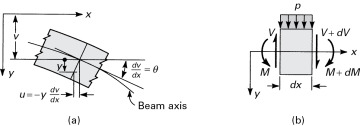
Figure 5.7. (a) Longitudinal displacements in a beam due to rotation of a plane section; (b) element between adjoining sections of a beam.
The slope is positive when clockwise, provided that the x and y axes have the directions shown. Since u is a linear function of y, this equation restates the kinematic hypothesis of the elementary theory of bending: Plane sections perpendicular to the longitudinal axis of the beam remain plane subsequent to bending. This assumption is confirmed by the exact theory only in the case of pure bending.
5.6.2 Method of Integration
In the next section, we obtain the stress distribution in a beam according to the elementary theory. We now derive some useful relations involving the shear force V, the bending moment M, the load per unit length p, the slope θ, and the deflection. Consider a beam element of length dx subjected to a distributed loading (Fig. 5.7b). Since dx is small, we omit the variation in the load per unit length p. In the free-body diagram, all the forces and the moments are positive. The shear force obeys the sign convention discussed in Section 1.4, while the bending moment is in agreement with the convention adopted in Section 5.2.
In general, the shear force and bending moment vary with the distance x, such that these quantities will have different values on each face of the element. The increments in shear force and bending moment are denoted by dV and dM, respectively. The equilibrium of forces in the vertical direction is governed by V − (V + dV) − p dx = 0 or
)
That is, the rate of change of shear force with respect to x is equal to the algebraic value of the distributed loading. Equilibrium of the moments about a z axis through the left end of the element, neglecting the higher-order infinitesimals, leads to
)
This relation states that the rate of change of bending moment is equal to the algebraic value of the shear force—a relation that is valid only if a distributed load or no load acts on the beam segment. Combining Eqs. (5.28) and (5.29), we have
)
The basic equation of bending of a beam, Eq. (5.10), combined with Eq. (5.30), may now be written as
)
For a beam of constant flexural rigidity EI, the beam equations derived here may be expressed as
)
These relationships also apply to wide beams provided that we substitute E/(1 − V2) for E (Table 3.1).
In many problems of practical importance, the deflection due to transverse loading of a beam may be obtained through successive integration of the beam equation:
)
Alternatively, we could begin with EIυ" = M(x) and integrate twice to obtain
)
In either case, the constants c1, c2, c3, and c4, which correspond to the homogeneous solution of the differential equations, may be evaluated from the boundary conditions. The constants c1, c2, c3/EI, and c4/EI represent the values at the origin of V, M, θ, and υ, respectively. In the method of successive integration, there is no need to distinguish between statically determinate and statically indeterminate systems (Section 5.11), because the equilibrium equations represent only two of the boundary conditions (on the first two integrals), and because the total number of boundary conditions is always equal to the total number of unknowns.
EXAMPLE 5.2 DISPLACEMENTS OF A CANTILEVER BEAM
A cantilever beam AB of length L and constant flexural rigidity EI carries a moment Mo at its free end A (Fig. 5.8a). Derive the equation of the deflection curve and determine the slope and deflection at A.
)
Figure 5.8. Example 5.2. (a) A cantilever beam is subjected to moment at its free end; (b) free-body diagram of part AO.
Solution From the free-body diagram of Fig. 5.8b, observe that the bending moment is +Mo throughout the beam. Thus, the third of Eqs. (5.32) becomes
Integration yields
The constant of integration c1 can be found from the condition that the slope is zero at the support; therefore, we have υ′(L) = 0 from which c1 = −MoL. The slope is then
)
Integrating, we obtain
The boundary condition on the deflection at the support is υ′(L) = 0 which yields c2 = MoL2/2EI. The equation of the deflection curve is thus a parabola:
)
However, every element of the beam experiences the same moments and deformation. The deflection curve should, therefore, be part of a circle. This inconsistency results from the use of an approximation for the curvature, Eq. (5.7). The error is very small, however, when the deformation υ is small [Ref. 5.1].
The slope and deflection at A are readily found by letting x = 0 in Eqs. (5.35) and (5.36):
)
The minus sign indicates that the angle of rotation is counterclockwise (Fig. 5.8a).