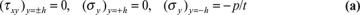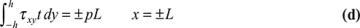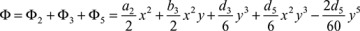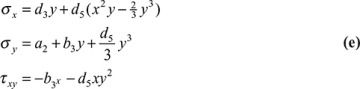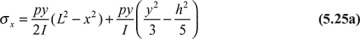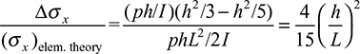- 5.1 Introduction
- 5.2 Pure Bending of Beams of Symmetrical Cross Section
- 5.3 Pure Bending of Beams of Asymmetrical Cross Section
- 5.4 Bending of A Cantilever of Narrow Section
- 5.5 Bending of a Simply Supported Narrow Beam
- 5.6 Elementary Theory of Bending
- 5.7 Normal and Shear Stresses
- 5.8 Effect of Transverse Normal Stress
- 5.9 Composite Beams
- 5.10 Shear Center
- 5.11 Statically Indeterminate Systems
- 5.12 Energy Method for Deflections
- 5.13 Elasticity Theory
- 5.14 Curved Beam Formula
- 5.15 Comparison of the Results of Various Theories
- 5.16 Combined Tangential and Normal Stresses
- References
- Problems
This chapter is from the book
This chapter is from the book
This chapter is from the book
5.5 Bending of a Simply Supported Narrow Beam
In this section, we consider the stress distribution in a narrow beam of thickness t and depth 2h subjected to a uniformly distributed loading (Fig. 5.6). The situation described here is one of plane stress, subject to the following boundary conditions, consistent with the origin of an x, y coordinate system located at midspan and midheight of the beam, as shown:
)
)
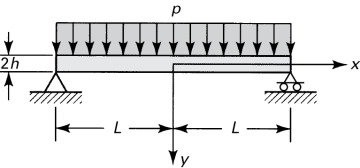
Figure 5.6. Bending of a simply supported beam with a uniform load.
Since no longitudinal load is applied at the ends, it would appear reasonable to state that σx = 0 at x = ± L. However, this boundary condition leads to a complicated solution, and a less severe statement is used instead:
)
The corresponding condition for bending couples at x = ±L is
)
For y equilibrium, it is required that
)
5.5.1 Use of Stress Functions
The problem is treated by superimposing the solutions Φ2,Φ3, and Φ5 (Section 3.6) with
We then have
)
The stresses are
)
The conditions (a) are
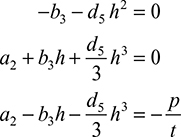
and the solution is
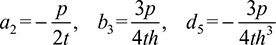
The constant d3 is obtained from condition (c) as follows:
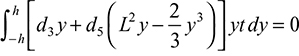
or
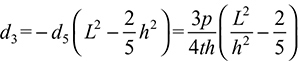
Expressions (e), together with the values obtained for the constants, also fulfill conditions (b) and (d).
The state of stress is thus represented by
)
)
)
where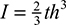 
is the area moment of inertia taken about a line through the centroid, parallel to the z axis. Although the solutions given by Eqs. (5.25) satisfy the equations of elasticity and the boundary conditions, they are not exact. We can see this by substituting x = ±L into Eq. (5.25a) to obtain the following expression for the normal distributed forces per unit area at the ends:
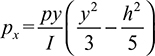
This state cannot exist, as no forces act at the ends. From Saint-Venant′s principle, however, we may conclude that the solutions do predict the correct stresses throughout the beam, except near the supports.
5.5.2 Comparison of the Results with the Elementary Theory Results
Recall that the longitudinal normal stress derived from elementary beam theory is σx = -My/I; this is equivalent to the first term of Eq. (5.25a). The second term is then the difference between the longitudinal stress results given by the two approaches. To gauge the magnitude of the deviation, consider the ratio of the second term of Eq. (5.25a) to the result of elementary theory at x = 0. At this point, the bending moment is a maximum. Substituting y = h for the condition of maximum stress, we obtain
)
For a beam of length 10 times its depth, this ratio is small,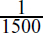 
. For beams of ordinary proportions, we can conclude that elementary theory provides a result of sufficient accuracy for σx. On the one hand, for σy, this stress is not found in the elementary theory. On the other hand, the result for τxy is the same as that yielded by elementary beam theory.
The displacement of the beam may be determined in a manner similar to that described for a cantilever beam (Section 5.4).
Part B: Approximate Solutions