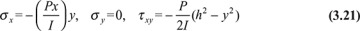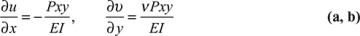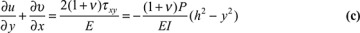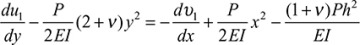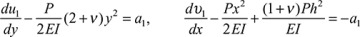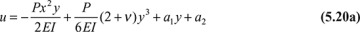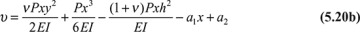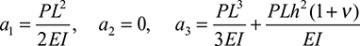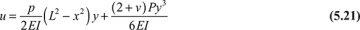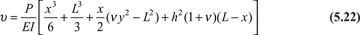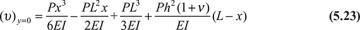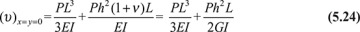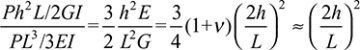- 5.1 Introduction
- 5.2 Pure Bending of Beams of Symmetrical Cross Section
- 5.3 Pure Bending of Beams of Asymmetrical Cross Section
- 5.4 Bending of A Cantilever of Narrow Section
- 5.5 Bending of a Simply Supported Narrow Beam
- 5.6 Elementary Theory of Bending
- 5.7 Normal and Shear Stresses
- 5.8 Effect of Transverse Normal Stress
- 5.9 Composite Beams
- 5.10 Shear Center
- 5.11 Statically Indeterminate Systems
- 5.12 Energy Method for Deflections
- 5.13 Elasticity Theory
- 5.14 Curved Beam Formula
- 5.15 Comparison of the Results of Various Theories
- 5.16 Combined Tangential and Normal Stresses
- References
- Problems
This chapter is from the book
This chapter is from the book
This chapter is from the book
5.4 Bending of A Cantilever of Narrow Section
Consider a narrow cantilever beam of rectangular cross section, loaded at its free end by a concentrated force of magnitude such that the beam weight may be neglected (Fig. 5.5). This situation may be regarded as a case of plane stress provided that the beam thickness t is small relative to the beam depth 2h. The distribution of stress in the beam, as we found in Example 3.1, is given by
)
)
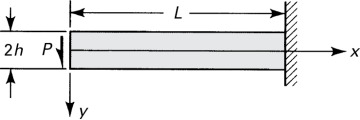
Figure 5.5. Deflections of an endloaded cantilever beam.
To derive expressions for the beam displacement, we must relate stress, described by Eq. (3.21), to strain. This is accomplished through the use of the strain-displacement relations and Hooke′s law:
)
)
Integration of Eqs. (a) and (b) yields
)
)
Differentiating Eqs. (d) and (e) with respect to y and x, respectively, and substituting into Eq. (c), we have
)
In this expression, note that the left and right sides depend only on y and x, respectively. These variables are independent of each other, so we conclude that the equation can be valid only if each side is equal to the same constant:
)
These are integrated to yield
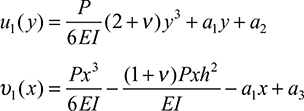
in which a2 and a3 are constants of integration. The displacements may now be written
)
)
The constants a1, a2, and a3 depend on known conditions. If, for example, the situation at the fixed end is such that
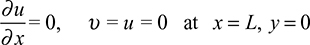
then, from Eqs. (5.20),
)
The beam displacement is therefore
)
)
On examining these equations, it becomes that u and υ do not obey a simple linear relationship with y and x. We conclude that plane sections do not, as assumed in elementary theory, remain plane subsequent to bending.
5.4.1 Comparison of the Results with the Elementary Theory Results
The vertical displacement of the beam axis is obtained by substituting y = 0 into Eq. (5.22):
)
Introducing this relation into Eq. (5.7), the radius of curvature is given by
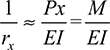
provided that dυ/dx is a small quantity. Once again, we obtain Eq. (5.9a), the beam curvature—moment relationship of elementary bending theory.
It is also a simple matter to compare the total vertical deflection at the free end (x = 0) with the deflection derived in elementary theory. Substituting x = 0 into Eq. (5.23), the total deflection is
)
where the deflection associated with shear is clearly Ph2L/2GI = 3PL/2GA. The ratio of the shear deflection to the bending deflection at x = 0 provides a measure of beam slenderness:
)
If, for example, L = 10(2h), the preceding quotient is only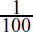 
. For a slender beam, 2h ≪ L and the deflection is mainly due to bending. In contrast, in cases involving vibration at higher modes, and in wave propagation, the effect of shear is of great importance in slender as well as in other beams.
In the case of wide beams (t≫2h), Eq. (5.24) must be modified by replacing E and ν as indicated in Table 3.1.