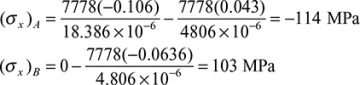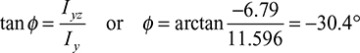- 5.1 Introduction
- 5.2 Pure Bending of Beams of Symmetrical Cross Section
- 5.3 Pure Bending of Beams of Asymmetrical Cross Section
- 5.4 Bending of A Cantilever of Narrow Section
- 5.5 Bending of a Simply Supported Narrow Beam
- 5.6 Elementary Theory of Bending
- 5.7 Normal and Shear Stresses
- 5.8 Effect of Transverse Normal Stress
- 5.9 Composite Beams
- 5.10 Shear Center
- 5.11 Statically Indeterminate Systems
- 5.12 Energy Method for Deflections
- 5.13 Elasticity Theory
- 5.14 Curved Beam Formula
- 5.15 Comparison of the Results of Various Theories
- 5.16 Combined Tangential and Normal Stresses
- References
- Problems
This chapter is from the book
This chapter is from the book
This chapter is from the book
5.3 Pure Bending of Beams of Asymmetrical Cross Section
In this section, we extend the discussion in Section 5.2 to the more general case in which a beam of arbitrary cross section is subjected to end couples My and Mz about the y and z axes, respectively (Fig. 5.3). Following a procedure similar to that described in Section 5.2, plane sections are again taken to remain plane. Assume that the normal stress σx acting at a point within dA is a linear function of the y and z coordinates of the point; assume further that the remaining stresses are zero. Then the stress field is
)
)
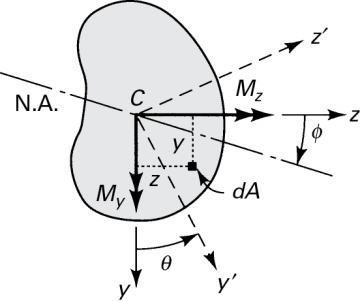
Figure 5.3. Pure bending of beams of asymmetrical cross section.
where c1, c2, c3 are constants to be evaluated.
The equilibrium conditions at the beam ends, as before, relate to the force and bending moment:
)
)
Carrying σx, as given by Eq. (5.11), into Eqs. (a), (b), and (c) results in the following expressions:
)
)
)
For the origin of the y and z axes to be coincident with the centroid of the section, it is required that
)
Based on Eq. (d), we conclude that c1 = 0; based on Eqs. (5.11), we conclude that σx = 0 at the origin. Thus, the neutral axis passes through the centroid, as in the beam of symmetrical section. In addition, the field of stress described by Eqs. (5.11) satisfies the equations of equilibrium and compatibility and the lateral surfaces are free of stress. Now consider the defining relationships
)
The quantities Iy and Iz are the moments of inertia about the y and z axes, respectively, and Iyz is the product of inertia about the y and z axes. From Eqs. (e) and (f), together with Eqs. (5.12), we obtain expressions for c2 and c3.
5.3.1 Stress Distribution
Substitution of the constants into Eqs. (5.11) results in the following generalized flexure formula:
)
The equation of the neutral axis is found by equating this expression to zero:
)
This is an inclined line through the centroid C. The angle ϕ between the neutral axis and the z axis is determined as follows:
)
The angle ϕ (measured from the z axis) is positive in the clockwise direction, as shown in Fig. 5.3. The highest bending stress occurs at a point located farthest from the neutral axis.
There is a specific orientation of the y and z axes for which the product of inertia Iyz vanishes. Labeling the axes so oriented as y′ and z′, we have Iy′z′ = 0. The flexure formula under these circumstances becomes
)
The y′ and z′ axes now coincide with the principal axes of inertia of the cross section, and we can find the stresses at any point by applying Eq. (5.13) or Eq. (5.16).
The kinematic relationships discussed in Section 5.2 are valid for beams of asymmetrical section provided that y and z represent the principal axes.
5.3.2 Transformation of Inertia Moments
Recall that the two-dimensional stress (or strain) and the moment of inertia of an area are second-order tensors (Section 1.17). Thus, the transformation equations for stress and moment of inertia are analogous (Section C.2.2). In turn, the Mohr′s circle analysis and all conclusions drawn for stress apply to the moment of inertia. With reference to the coordinate axes shown in Fig. 5.3, applying Eq. (C.12a), the moment of inertia about the y′ axis is
)
From Eq. (C.13), the orientation of the principal axes is given by
)
The principal moments of inertia, I1 and I2 from Eq. (C.14) are
)
where the subscripts 1 and 2 refer to the maximum and minimum values, respectively.
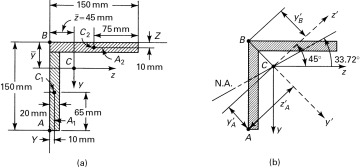
Determination of the moments of inertia and stresses in an asymmetrical section is illustrated in Example 5.1.
EXAMPLE 5.1 ANALYSIS OF AN ANGLE IN PURE BENDING
A 150- by 150-mm slender angle of 20-mm thickness is subjected to oppositely directed end couples Mz = 11 KN·m at the centroid of the cross section. What bending stresses exist at points A and B on a section away from the ends (Fig. 5.4a)? Determine the orientation of the neutral axis.
)
Figure 5.4. Example 5.1. An equal-leg-angle cross section of beam.
Solution Equations (5.13) and (5.16) are applied to obtain the normal stress. This requires first determining a number of section properties through the use of familiar expressions of mechanics given in Appendix C. The computer program presented in Table C.2 provides a check of the numerical values obtained here for the area characteristics and may be extended to compute the stresses.
Location of the Centroid C. Let 
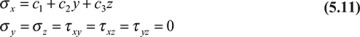
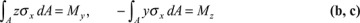
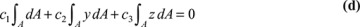
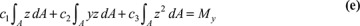
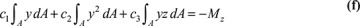
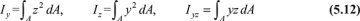
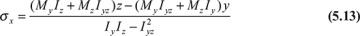
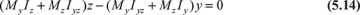
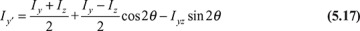
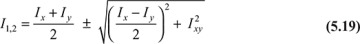
and 
represent the distances from C to arbitrary reference lines (denoted as Z and Y):
)
where 
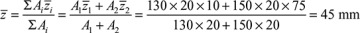
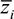represents the z distance from the Y reference line to the centroid of each subarea (A1 and A2) composing the total cross section. Since the section is symmetrical,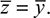 
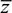Moments and Products of Inertia. For a rectangular section of depth h and width b, the moment of inertia about the neutral 
axis is 
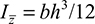(Table C.1). We now use the yz axes as reference axes through C. Representing the distances from C to the centroids of each subarea by dy1, dy2, dz1, and dz2 we obtain the moments of inertia with respect to these axes using the parallel-axis theorem. Applying Eq. (C.9),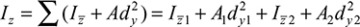
)
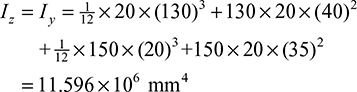
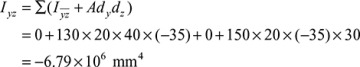
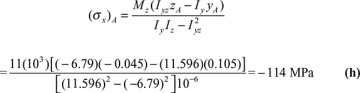
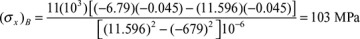
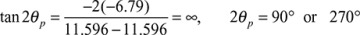
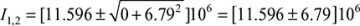
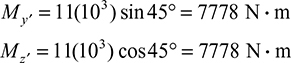
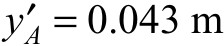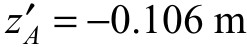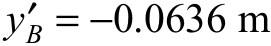Thus, referring to Fig. 5.4a,
The transfer formula, Eq. (C.11), for a product of inertia yields
)
Stresses Using Eq. (5.13). We have yA = 0.105 m, yB = −0.045 m, zA = −0.045 m, zB = 0.045 m, and My = 0. Hence,
)
Similarly,
)
Alternatively, these stresses may be calculated as described next.
Directions of the Principal Axes and the Principal Moments of Inertia. Employing Eq. (5.18), we have
)
Therefore, the two values of θp are 45° and 135° Substituting the first of these values into Eq. (5.17), we obtain Iy′ = [11.596 + 6.79 sin 90°]. Since the principal moments of inertia are, by application of Eq. (5.19),
)
we see that I1 = Iy′ = 18.386×106 mm4 and I2 = Iz′ = 4.806×106 mm4. The principal axes are indicated in Fig. 5.4b as the y′z' axes.
Stresses Using Eq. (5.16). The components of bending moment about the principal axes are
Equation (5.16) is now applied, referring to Fig 5.4b, with 
, 
, 
, and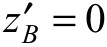 
determined from geometric considerations:
)
as before.
Direction of the Neutral Axis. From Eq. (5.15), with My = 0,
)
The negative sign indicates that the neutral is located counterclockwise from the z axis (Fig. 5.4b).