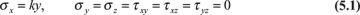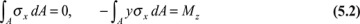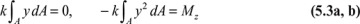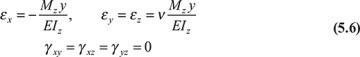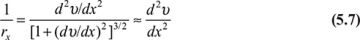- 5.1 Introduction
- 5.2 Pure Bending of Beams of Symmetrical Cross Section
- 5.3 Pure Bending of Beams of Asymmetrical Cross Section
- 5.4 Bending of A Cantilever of Narrow Section
- 5.5 Bending of a Simply Supported Narrow Beam
- 5.6 Elementary Theory of Bending
- 5.7 Normal and Shear Stresses
- 5.8 Effect of Transverse Normal Stress
- 5.9 Composite Beams
- 5.10 Shear Center
- 5.11 Statically Indeterminate Systems
- 5.12 Energy Method for Deflections
- 5.13 Elasticity Theory
- 5.14 Curved Beam Formula
- 5.15 Comparison of the Results of Various Theories
- 5.16 Combined Tangential and Normal Stresses
- References
- Problems
5.2 Pure Bending of Beams of Symmetrical Cross Section
The simplest case of pure bending is that of a beam possessing a vertical axis of symmetry, subjected to equal and opposite end couples (Fig. 5.1a). The semi-inverse method is now applied to analyze this problem. The moment M z shown in Fig. 5.1a is defined as positive, because it acts on a positive (negative) face with its vector in the positive (negative) coordinate direction. This sign convention agrees with that of stress (Section 1.5). We will assume that the normal stress over the cross section varies linearly with y and that the remaining stress components are zero:

Figure 5.1. (a) Beam of singly symmetric cross section in pure bending; (b) stress distribution across cross section of the beam.
Here k is a constant, and y = 0 contains the neutral surface—that is, the surface along which σx = 0 The intersection of the neutral surface and the cross section locates the neutral axis (abbreviated NA). Figure 5.1b shows the linear stress field in a section located an arbitrary distance a from the left end.
Since Eqs. (5.1) indicate that the lateral surfaces are free of stress, we need only be assured that the stresses are consistent with the boundary conditions at the ends. These conditions of equilibrium require that the resultant of the internal forces be zero and that the moments of the internal forces about the neutral axis equal the applied moment
where A is the cross-sectional area. Note that the zero stress components τxy, τxz in Eqs. (5.1) satisfy the conditions that no y- and z-directed forces exist at the end faces. Moreover, because of the y symmetry of the section, σx = ky produces no moment about the y axis. The negative sign in the second expression implies that a positive moment mz is one that results in compressive (negative) stress at points of positive y. Substituting Eqs. (5.1) into Eqs. (5.2) yields
Since k ≠ 0, Eq. (5.3a) indicates that the first moment of cross-sectional area about the neutral axis is zero. This requires that the neutral and centroidal axes of the cross section coincide. Neglecting body forces, it is clear that the equations of equilibrium (3.4), are satisfied by Eqs. (5.1). It can also readily be verified that Eqs. (5.1) together with Hooke's law fulfill the compatibility conditions, Eq. (2.12). Thus, Eqs. (5.1) represent an exact solution.
The integral in Eq. (5.3b) defines the moment of inertia Iz of the cross section about the z axis of the beam cross section (Appendix C); therefore,
An expression for normal stress can now be written by combining Eqs. (5.1) and (a):
This is the familiar elastic flexure formula applicable to straight beams.
Since, at a given section, M and I are constant, the maximum stress is obtained from Eq. (5.4) by taking |y|max = c:
where S is the elastic section modulus. Equation (5.5) is widely employed in practice because of its simplicity. To facilitate its use, section moduli for numerous common sections are tabulated in various handbooks. A fictitious stress in extreme fibers, computed from Eq. (5.5) for the experimentally obtained ultimate bending moment (Section 12.7), is termed the modulus of rupture of the material in bending. This quantity, σmax=Mu/S, is frequently used as a measure of the bending strength of materials.
5.2.1 Kinematic Relationships
To gain further insight into the beam problem, we now consider the geometry of deformation—that is, beam kinematics. Fundamental to this discussion is the hypothesis that sections originally plane remain so subsequent to bending. For a beam of symmetrical cross section, Hooke′s law and Eq. (5.4) lead to
where EIz is the flexural rigidity.
Let us examine the deflection of the beam axis, whose axial deformation is zero. Figure 5.2a shows an element of an initially straight beam, now in a deformed state. Because the beam is subjected to pure bending, uniform throughout, each element of infinitesimal length experiences identical deformation, with the result that the beam curvature is everywhere the same. The deflected axis of the beam or the deflection curve is thus shown deformed, with radius of curvature rx. The curvature of the beam axis in the xy plane in terms of the y deflection υ is
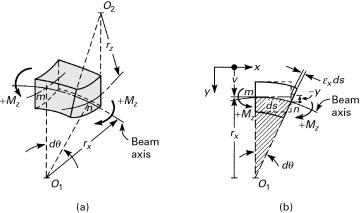
Figure 5.2. (a) Segment of a bent beam; (b) geometry of deformation.
where the approximate form is valid for small deformations (dυ/dx≪1). The sign convention for curvature of the beam axis is such that this sign is positive when the beam is bent concave downward, as shown in the figure.
As shown by the geometry in Fig. 5.2b, the shaded sectors are similar. Hence, the radius of curvature and the strain are related as follows:
where ds is the arc length mn along the longitudinal axis of the beam. For a small displacement, ds ≈ dx and θ represents the slope dυ/dx of the beam axis. Clearly, for the positive curvature shown in Fig. 5.2a, θ increases as we move from left to right along the beam axis. On the basis of Eqs. (5.6) and (5.8),
Following a similar procedure and noting that εz ≈ -Vεx, we may also obtain the curvature in the yz plane as
The basic equation of the deflection curve of a beam is obtained by combining Eqs. (5.7) and (5.9a) as follows:
This expression, relating the beam curvature to the bending moment, is known as the Bernoulli—Euler law of elementary bending theory. It is observed from Fig. 5.2 and Eq. (5.10) that a positive moment produces a positive curvature. If the sign convention adopted in this section for either moment or deflection (and curvature) is reversed, the plus sign in Eq. (5.10) should likewise be reversed.
Reference to Fig. 5.2a reveals that the top and bottom lateral surfaces have been deformed into saddle-shaped or anticlastic surfaces of curvature 1/rz. The vertical sides have been simultaneously rotated as a result of bending. Examining Eq. (5.9b) suggests a method for determining Poisson’s ratio [Ref. 5.1]. For a given beam and bending moment, a measurement of 1/rz leads directly to v. The effect of anticlastic curvature is small when the beam depth is comparable to its width.
5.2.2 Timoshenko Beam Theory
The Timoshenko theory of beams, developed by S. P. Timoshenko at the beginning of the twentieth century, constitutes an improvement over the Euler—Bernoulli theory. In the static case, the difference between the two hypotheses is that the former includes the effect of shear stresses on the deformation by assuming a constant shear over the beam height, whereas the latter ignores the influence of transverse shear on beam deformation. The Timoshenko theory is also said to be an extension of the ordinary beam theory that allows for the effect of the transverse shear deformation while relaxing the assumption that plane sections remain plane and normal to the deformed beam axis.
The Timoshenko beam theory is well suited to describing the behavior of short beams and sandwich composite beams. In the dynamic case, the theory incorporates shear deformation as well as rotational inertia effects, and it will be more accurate for not very slender beams. By effectively taking into account the mechanism of deformation, Timoshenko′s theory lowers the stiffness of the beam, with the result being a larger deflection under static load and lower predicted fundamental frequencies of vibration for a prescribed set of boundary conditions.