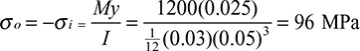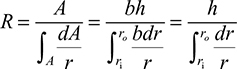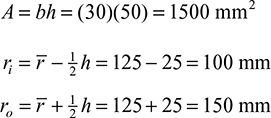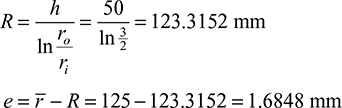- 5.1 Introduction
- 5.2 Pure Bending of Beams of Symmetrical Cross Section
- 5.3 Pure Bending of Beams of Asymmetrical Cross Section
- 5.4 Bending of A Cantilever of Narrow Section
- 5.5 Bending of a Simply Supported Narrow Beam
- 5.6 Elementary Theory of Bending
- 5.7 Normal and Shear Stresses
- 5.8 Effect of Transverse Normal Stress
- 5.9 Composite Beams
- 5.10 Shear Center
- 5.11 Statically Indeterminate Systems
- 5.12 Energy Method for Deflections
- 5.13 Elasticity Theory
- 5.14 Curved Beam Formula
- 5.15 Comparison of the Results of Various Theories
- 5.16 Combined Tangential and Normal Stresses
- References
- Problems
This chapter is from the book
This chapter is from the book
This chapter is from the book
5.15 Comparison of the Results of Various Theories
We now examine the solutions obtained in Sections 5.13 and 5.14 with results determined using the flexure formula for straight beams. To do so, we consider a curved beam of rectangular cross section and unit thickness experiencing pure bending. The tangential stress predicted by the elementary theory (based on a linear distribution of stress) is My/I. The Winkler approach, which leads to a hyperbolic distribution, is given by Eq. (5.70) or Eq. (5.71), while the exact theory results in Eqs. (5.67). In each case, the maximum and minimum values of stress are expressed by
)
Table 5.4 lists values of m as a function of b/a for the four cases cited [Ref. 5.1], in which b = ro and a = rj (see Figs. 5.24 and 5.25). As can be seen, there is good agreement between the exact and Winkler results. On this basis, as well as from more extensive comparisons, we may conclude that the Winkler approach is adequate for practical applications. Its advantage lies in the relative ease with which it may be applied to any symmetric section.
Table 5.4. The Values of m for Typical Ratios of Outer Radius b to Inner Radius a
|
|
Curved Beam Formula |
Elasticity Theory |
||
|---|---|---|---|---|---|
b/a |
Flexure Formula |
r = a |
r = b |
r = a |
r = b |
1.3 |
±66.67 |
−72.980 |
61.270 |
−73.050 |
61.350 |
1.5 |
±24.00 |
−26.971 |
20.647 |
−27.858 |
21.275 |
2.0 |
±6.00 |
−7.725 |
4.863 |
−7.755 |
4.917 |
3.0 |
±1.50 |
−2.285 |
1.095 |
−2.292 |
1.130 |
The agreement between the Winkler approach and the exact analyses is not as good in situations involved combined loading as it is for the case of pure bending. As might be expected, for beams of only slight curvature, the simple flexure formula provides good results while requiring only simple computation. The linear and hyperbolic stress distributions are approximately the same for b/a = 1.1. As the curvature of the beam increases, (b/a > 1.3) the stress on the concave side rapidly increases over the one given by the flexure formula.
5.15.1 Correction of σθ for Beams with Thin-Walled Cross Sections
Where I-beams, T-beams, or thin-walled tubular curved beams are involved, the approaches developed in this chapter will not accurately predict the stresses in the system. The error in such cases is attributable to the high stresses existing in certain sections such as the flanges, which cause significant beam distortion. A modified Winkler’s equation can be applied in such situations if more accurate results are required [Ref. 5.6]. The distortion, and thus the error in σθ, is reduced when the flange thickness is increased. Given that material yielding is highly localized, its effect is not of concern unless the curved beam is under fatigue loading.
EXAMPLE 5.13 MAXIMUM STRESS IN A CURVED RECTANGULAR BAR
A rectangular aluminum bar having mean radius 
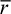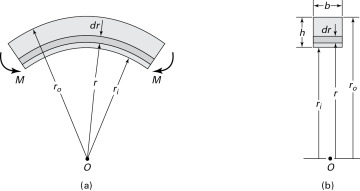
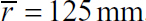carries end moments M, as illustrated in Fig. 5.26. Calculate the stresses in the member using (a) the flexure formula and (b) the curved beam formula.
)
Figure 5.26. Example 5.13. (a) Rectangular curved beam in pure bending; (b) cross section.
Given: M = 1.2 KN·m, b = 30 mm, h = 50 mm and 
.
Solution The subscripts i and o refer to the quantities of the inside and outside fibers, respectively.
Applying the flexure formula, Eq. (5.38) with y = hl2, we obtain
This is the result we would get for a straight beam.
We first derive the expression for the radius R of the neutral axis. From Fig. 5.26, A = bh and dA = bdr. Integration of Eq. (5.68) between the limits ri and ro results in
)
or
)
The given data lead to
Then, Eqs. (5.73) and (5.69) yield, respectively,
Note that the radius of the neutral axis R must be calculated with five significant figures.
The maximum compressive and tensile stresses are calculated by using Eq. (5.70) as follows:
)
){kind=link}
){kind=link}
The negative sign means a compressive stress.
Comment The maximum stress 96 MPa obtained in part (a) by the flexure formula represents an error of about 13% from the more accurate value for the maximum stress (110.7 MPa) found in part (b).