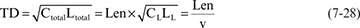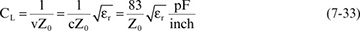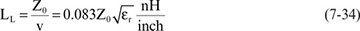- 7.1 Forget the Word Ground
- 7.2 The Signal
- 7.3 Uniform Transmission Lines
- 7.4 The Speed of Electrons in Copper
- 7.5 The Speed of a Signal in a Transmission Line
- 7.6 Spatial Extent of the Leading Edge
- 7.7 “Be the Signal”
- 7.8 The Instantaneous Impedance of a Transmission Line
- 7.9 Characteristic Impedance and Controlled Impedance
- 7.10 Famous Characteristic Impedances
- 7.11 The Impedance of a Transmission Line
- 7.12 Driving a Transmission Line
- 7.13 Return Paths
- 7.14 When Return Paths Switch Reference Planes
- 7.15 A First-Order Model of a Transmission Line
- 7.16 Calculating Characteristic Impedance with Approximations
- 7.17 Calculating the Characteristic Impedance with a 2D Field Solver
- 7.18 An n-Section Lumped-Circuit Model
- 7.19 Frequency Variation of the Characteristic Impedance
- 7.20 The Bottom Line
- End-of-Chapter Review Questions
7.15 A First-Order Model of a Transmission Line
An ideal transmission line is a new ideal circuit element that has the two special properties of a constant instantaneous impedance and a time delay associated with it. This ideal model is a “distributed” model in the sense that the properties of an ideal transmission line are distributed over its length rather than being concentrated in a single lumped point.
Physically, a controlled-impedance transmission line is composed of just two conductors with length and having a uniform cross section for the whole length. Earlier in this chapter, we introduced a zeroth-order model, which described a transmission line as a collection of capacitors spaced some distance apart. This was a physical model, not an equivalent electrical model.
We can further approximate the physical transmission line by describing the sections of signal- and return-path conductors as a loop inductance. The simplest equivalent circuit model for a transmission line would have small capacitors separated by small loop inductors, as shown in Figure 7-29. The C is the capacitance between the conductors, and the L is the loop inductance between the sections.
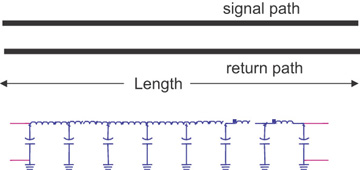
Figure 7-29 Top: Physical structure of a uniform transmission line. Bottom: First-order equivalent circuit model approximation for a transmission line based on combinations of Ls and Cs.
Each segment of the signal path has some partial self-inductance associated with it, and each segment of the return path has some partial self-inductance associated with it. There is some partial mutual inductance between each of the signal- and return-path segments between the discrete capacitors. For an unbalanced transmission line, such as a microstrip, the partial self-inductances of the signal- and return-path segments are different. In fact, the partial self-inductance of the signal path can be more than 10 times larger than the partial self-inductance of the return path.
However, from a signal’s perspective as it propagates down the line, it is a current loop, from the signal to the return path, that propagates. In this sense, all the signal current sees is the loop inductance down the signal-path segment and returning back through the return-path segment. For signal propagation in a transmission line and most cross-talk effects, the partial inductances of the signal and return paths do not play a role. It is only the loop inductance that is important. When approximating an ideal distributed-transmission line as a series of LC segments, the inductance the signal sees, as represented in the model, is really a loop inductance.
In the extreme, when each capacitor and inductor is infinitesimal and there is an infinite number of elements, there is a uniform capacitance per length, CL, and a uniform loop inductance per length, LL. These are often called the line parameters of a transmission line. Given the total length of the line, Len, the total capacitance is given by:
and the total inductance is given by:
where:
CL = capacitance per length
LL = loop inductance per length
Len = length of the transmission line
Just by looking at this LC circuit, it is difficult to get a feel for how a signal will interact with it. At first glance, we might think there will be a lot of oscillations and resonances. But what happens when the size of each element is infinitely small?
The only way to really know how a signal will interact with this circuit model is to apply network theory and solve the differential equations represented by this LC network. The results indicate that a signal traveling down the network will see a constant instantaneous impedance at each node. This constant instantaneous impedance is the same as the instantaneous impedance we discovered for an ideal distributed-transmission-line element. The instantaneous impedance is numerically the characteristic impedance of the line. Likewise, there will be a finite delay between the time the signal is introduced into the front of the LC network and the time it comes out.
Using network theory, we can calculate how the characteristic impedance and time delay depend on the line parameters and total length of the line:
where:
Z0 = characteristic impedance, in Ohms
LL = loop inductance per length of the transmission line
CL = capacitance per length of the transmission line
TD = time delay of the transmission line
Ltotal = total loop inductance in the transmission line
Ctotal = total capacitance in the transmission line
v = speed of the signal in the transmission line
Without having to invoke a finite speed for the propagation of a signal down a transmission line, the electrical properties of an LC network predict this behavior. Likewise, though it is hard to tell by looking at the circuit model, network theory predicts that there is a constant impedance the signal sees at each node along the circuit.
These two predicted properties—the characteristic impedance and the time delay—must match the same values we derived based on the zeroth-order physics model of finite speed and collection of capacitor buckets. By combining the results from these two models, a number of very important relationships can be derived.
Because the speed of a signal depends on the dielectric constant of the material and on the capacitance per length and inductance per length, we can relate the capacitance per length to the inductance per length:
From the relationship between the characteristic impedance and velocity, the following relationships can be derived:
And, from the time delay and the characteristic impedance of the transmission line, the following can be derived:
where:
Z0 = characteristic impedance, in Ohms
LL = loop inductance per length of the transmission line, in nH/inch
CL = capacitance per length of the transmission line, in pF/inch
TD = time delay of the transmission line, in nsec
Ltotal = total loop inductance in the transmission line, in nH
Ctotal = total capacitance in the transmission line, in pF
v = speed of the signal in the transmission line, in in/nsec
For example, a line that is 50 Ohms and has a dielectric constant of 4 has a capacitance per length of CL = 83/50 × 2 = 3.3 pF/inch. This is a startling conclusion.
If the line width doubles, the dielectric spacing would have to double to maintain the same characteristic impedance, and the capacitance would stay the same. An interconnect in a BGA package that has been designed as a 50-Ohm controlled-impedance line, 0.5 inches long, has a capacitance of 3.3 pF/inch × 0.5 inch = 1.6 pF.
Likewise, the inductance per length of a 50-Ohm line made with FR4 is LL = 0.083 × 50 × 2 = 8.3 nH/inch.
If the time delay of a line is 1 nsec and it is 50 Ohms, the total capacitance in the line is Ctotal = 1 nsec/50 = 20 pF. If the line is 6 inches long, this 20 pF of capacitance is distributed over 6 inches and the capacitance per length is 20 pF/6 inches = 3.3 pF/inch. For this same line, the total loop inductance going down the signal line and looping back through the return path is Ltotal = 1 nsec × 50 Ohms = 50 nH. Distributed over the 6 inches of length, this is an inductance per length of 50 nH/6 inches = 8.3 nH/inch.
These relationships that relate the capacitance, inductance, characteristic impedance, and dielectric constant, which are associated with a transmission line, apply to any transmission line. They make no assumptions on the cross-section geometry. They are very powerful tools to help us estimate one or more of these terms using existing approximations or field solvers. If we know any two, we can always find the others.
It is tempting to consider this LC model of a transmission line as representing how a real transmission line behaves. If we ignore the inductance, for example, we might consider a real transmission line as just some capacitance. Won’t we see an RC charging time for the transmission line when driven by the output impedance of a driver?
In fact, a real transmission line is not just a capacitor, or even just an inductor; it is a distributed LC interconnect. It is the adjacent L and C, microscopically small in size, which transforms this interconnect into a new behavior. A fast edge entering the interconnect maintains this rise time throughout the interconnect.
As the fast edge propagates, it does not see the capacitance and a need to charge it through an RC, nor does it see an L and a slower rise time as the L/R. Rather, it sees a brand-new emergent property of an instantaneous impedance that supports any rise-time signal. A transmission line does not look like an L or a C to the signal edge; it looks like a resistive element.
It is possible to calculate the total capacitance and total loop inductance in a transmission line interconnect, but it would be incorrect to think of the transmission line as just a C or just an L. They are forever connected together, and both elements are equally important.
Of course, this lumped-circuit LC ladder model is just an approximation. Instead of thinking of a real transmission line in terms of the LC ladder model, recalibrate your engineering intuition to see a transmission line as a brand-new ideal circuit element with the new, emergent behavior of supporting any rise-time signal once launched and seeing an instantaneous impedance.