- 7.1 Forget the Word Ground
- 7.2 The Signal
- 7.3 Uniform Transmission Lines
- 7.4 The Speed of Electrons in Copper
- 7.5 The Speed of a Signal in a Transmission Line
- 7.6 Spatial Extent of the Leading Edge
- 7.7 “Be the Signal”
- 7.8 The Instantaneous Impedance of a Transmission Line
- 7.9 Characteristic Impedance and Controlled Impedance
- 7.10 Famous Characteristic Impedances
- 7.11 The Impedance of a Transmission Line
- 7.12 Driving a Transmission Line
- 7.13 Return Paths
- 7.14 When Return Paths Switch Reference Planes
- 7.15 A First-Order Model of a Transmission Line
- 7.16 Calculating Characteristic Impedance with Approximations
- 7.17 Calculating the Characteristic Impedance with a 2D Field Solver
- 7.18 An n-Section Lumped-Circuit Model
- 7.19 Frequency Variation of the Characteristic Impedance
- 7.20 The Bottom Line
- End-of-Chapter Review Questions
7.11 The Impedance of a Transmission Line
What impedance does a battery see when connected to the front of a transmission line? As soon as the battery is connected to the transmission line, the voltage signal sees the instantaneous impedance of the transmission line, and the signal starts propagating down the line. As long as the signal continues to propagate, the input impedance always looks like the instantaneous impedance, which is the characteristic impedance.
The impedance the battery sees when looking into the line is thus the same as the instantaneous impedance of the line—as long as the signal is propagating down the line. It looks like a resistor, and the current into the line is directly proportional to the voltage applied.
A circuit element that has a constant current through it for a constant voltage applied is an ideal resistor. From the battery’s perspective, when the terminals are attached to the front end of the line and the signal propagates down the line, the transmission line draws a constant current and acts like a resistor to the battery. The impedance of the transmission line, as seen by the battery, is a constant resistance, as long as the signal is propagating down the line. There is no test the battery can do that to distinguish the transmission line from a resistor, at least while the signal is propagating down and back on the line.
What does it mean to refer to the impedance of a cable? An RG58 cable is often referred to as a 50-Ohm cable. What does this really mean? Suppose we were to take a 3-foot length of RG58 cable and measure the impedance at the front end, between the signal and return paths. What impedance will we measure? Of course, we can measure the impedance with an Ohmmeter. If we connect an Ohmmeter to the front end of the 3-foot transmission line, between the central signal line and the outer shield, as shown in Figure 7-13, what will it read? Will it be an open, a short, or 50 Ohms?
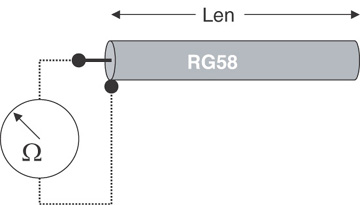
Figure 7-13 Measuring the input impedance of a length of RG58 cable with an Ohmmeter.
Let’s be more specific. Suppose we were to measure the impedance using a digital multimeter (DMM) with a liquid crystal display (LCD) that updates in a second. What impedance will be measured?
Of course, if we wait long enough, the short length of cable will look like an open, and we would measure infinite as the input impedance. So, if the input impedance of this short cable is infinite, what does it mean to have a 50-Ohm cable? Where does the characteristic-impedance attribute come in?
To explore this further, consider a more extreme, very long length of RG58 cable. It’s so long, in fact, that the line stretches from the earth to the moon. This is about 240,000 miles long. As we might recall from high school, the speed of light in a vacuum is about 186,000 miles per second, or close to 130,000 miles per second in the dielectric of the RG58 cable. It would take light about 2 seconds to go from one end of the cable to the far end and another 2 seconds to come back. If we attach our DMM to the front end of this long line, what will it see as the impedance? Remember, the DMM finds the resistance by connecting a 1-volt source to the device under test and measuring the ratio of the voltage applied to the current draw.
This is exactly the case of driving a transmission line, provided that we do the impedance measurement in less than the 4-second round-trip time of flight. During the first 4 seconds, while the signal is propagating out to the end of the interconnect and back, the current into the front of the line will be a constant amount equal to the current required by the signal to charge up successive sections of the cable as it propagates outward.
The impedance the source sees looking into the front of the line, the “input” impedance, will be the same as the instantaneous impedance the signal sees, which is the characteristic impedance of the line. In fact, the source won’t know that there is an end to the transmission line until a round-trip time of flight, or 4 seconds, later. During the first 4 seconds of measurement, the Ohmmeter should read the characteristic impedance of the line, or 50 Ohms, in this case.
But we know that if we wait a day with the Ohmmeter connected, we will eventually measure the input impedance of the cable to be an open. Here are the two extremes: Initially, we measure 50 Ohms, but after a long time, we measure an open. So, what is the input impedance of the line?
The answer is that there is no one value. It is time dependent; it changes. This example illustrates that the input impedance of a transmission line is time dependent; it depends on how long we are doing the measurement compared to the round-trip time of flight. This is illustrated in Figure 7-14. Within the round-trip time of flight, the impedance looking into the front end of the transmission line is the characteristic impedance of the line. After the round-trip time of flight, the input impedance can be anywhere from infinite to zero, depending on what is at the far end of the transmission line.
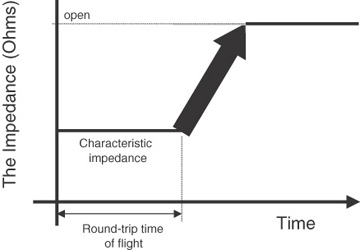
Figure 7-14 The input impedance, looking into a transmission line, is time dependent. During the round-trip time of flight, the measured input impedance will be the characteristic impedance. If we wait long enough, the input impedance will look like an open.
When we refer to the impedance of a cable or a line as being 50 Ohms, we are really saying the instantaneous impedance a signal would see propagating down the line is 50 Ohms. Or, the characteristic impedance of the line is 50 Ohms. Or, initially, if we look for a time, short compared to a round-trip time of flight, we will see 50 Ohms as the input impedance of the interconnect.
Even though these words sound similar, there is an important difference between the impedance, the input impedance, the instantaneous impedance, and the characteristic impedance of an interconnect. Just saying “the impedance” is ambiguous.
The instantaneous impedance of the transmission line is the impedance the signal sees as it propagates down the line. If the cross section is uniform, the instantaneous impedance will be the same down the line. However, it may change where there are discontinuities, for example, at the end. If the end is open, the signal will see an infinite instantaneous impedance when it hits the end of the line. If there is a branch, it will see a drop in the instantaneous impedance at the branch point.
The characteristic impedance of the interconnect is a physical quality of a uniform transmission line that characterizes the transmission line due to its geometry and material properties. It is equal to the one value of instantaneous impedance the signal would see as it propagates down the uniform cross section. If the transmission line is not uniform, the instantaneous impedance changes, and there is not one impedance that characterizes the line. A characteristic impedance applies only to a uniform transmission line.
Everyone who works in the signal-integrity field gets lazy sometimes and just uses the term impedance. We therefore must ask the qualifying question of which impedance we mean or look at the context of its use to know which of these three impedances we are referring to. Knowing the distinction, we can all try to use the right one and be less ambiguous.
When the rise time is shorter than the round-trip time of flight of an interconnect, a driver will see the interconnect with a resistive input impedance equal to the characteristic impedance of the line during the rising edge. Even though the line may be open at the far end, during the transition time, the front of the line will behave like a resistor.
The round-trip time of flight is related to the dielectric constant of the material and the length of the line. With rise times for most drivers in the sub-nanosecond regime, any interconnect longer than a few inches will look long and behave like a resistive load to the driver during the transition. This is one of the important reasons that the transmission line behavior of all interconnects must be considered.
Given this criterion, virtually all interconnects in high-speed digital systems will behave like transmission lines, and these properties will dominate the signal-integrity effects. For a transmission line on a board that is 3 inches long, the round-trip time of flight is about 1 nsec. If the integrated circuit (IC) driving the line has a rise time less than 1 nsec, the impedance it will see looking into the front of the line during the rising or falling edge will be the characteristic impedance of the line. The driver IC will see an impedance that acts resistive. If the rise time is very much longer than 1 nsec, it will see the impedance of the line as an open. If the rise time of the signal is somewhere between, the driver will see a very complicated, changing impedance as the edge bounces around between the low impedance driver and the open receiver. The received voltage can often be analyzed only using simulation tools. These tools are described in Chapter 8 “Transmission Lines and Reflections.”
The round-trip time of flight is a very important parameter of a transmission line. To a driver, the line will seem resistive for this time. Figure 7-15 shows the round-trip time of flight for various-length transmission lines made with air (εr = 1), FR4 (εr = 4), and ceramic (εr = 10) dielectric materials. In most systems with clock frequencies higher than 200 MHz, the rise time is less than 0.5 nsec. For these systems, all transmission lines longer than about 1.5 inches will appear resistive during the rise time. This means for virtually all high-speed drivers, when they drive a transmission line during the transition, the input impedance they see will act like a resistor.
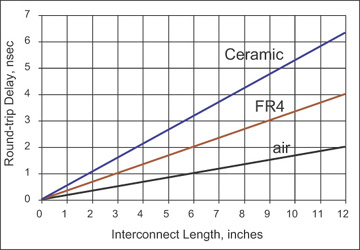
Figure 7-15 For a time equal to the round-trip time of flight, a driver will see the input impedance of the interconnect as a resistive load with a resistance equal to the characteristic impedance of the line.

