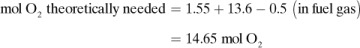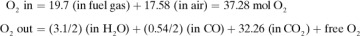- 1.0 Chapter Objectives
- 1.1 Classification of Transport Processes and Separation Processes (Unit Operations)
- 1.2 SI System of Basic Units Used in This Text and Other Systems
- 1.3 Methods of Expressing Temperatures and Compositions
- 1.4 Gas Laws and Vapor Pressure
- 1.5 Conservation of Mass and Material Balances
- 1.6 Energy and Heat Units
- 1.7 Conservation of Energy and Heat Balances
- 1.8 Numerical Methods for Integration
- 1.9 Chapter Summary
- Problems
- References
- Notation
1.5 Conservation of Mass and Material Balances
1.5A Conservation of Mass
One of the basic laws of physical science is the law of conservation of mass. This law, stated simply, says that mass cannot be created or destroyed (excluding, of course, nuclear or atomic reactions). Hence, the total mass (or weight) of all materials entering any process must equal the total mass of all materials leaving plus the mass of any materials accumulating or left in the process:
In many cases, there will be no accumulation of materials in a process, and in those cases the input will simply equal the output. Stated in other words, “what goes in must come out.” We call this type of process a steady-state process:
1.5B Simple Material Balances
In this section, we do simple material (weight or mass) balances in various processes at steady state with no chemical reaction occurring. We can use units of kg, lbm, lb mol, g, kg mol, and so on, in our balances. The reader is cautioned to be consistent and not to mix several units in a balance. When chemical reactions occur in the balances (as discussed in Section 1.5D), one should use kg mol units, since chemical equations relate moles reacting. In Chapter 4, overall mass balances will be covered in more detail and in Chapter 8, differential mass balances will be covered.
To solve a material-balance problem, it is advisable to proceed by a series of definite steps, as listed below:
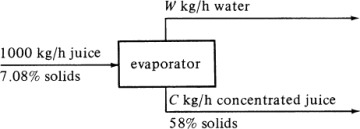
Sketch a simple diagram of the process. This can be a simple box diagram showing each stream entering by an arrow pointing in and each stream leaving by an arrow pointing out. Include on each arrow the compositions, amounts, temperatures, and so on, of that stream. All pertinent data should be on this diagram.
Write the chemical equations involved (if any).
Select a basis for calculation. In most cases, the problem is concerned with a specific amount of one of the streams in the process, which is selected as the basis.
Make a material balance. The arrows into the process will be input items and the arrows going out will be output items. The balance can be a total material balance as in Eq. (1.5-2) or a balance on each component present (if no chemical reaction occurs).
Typical processes that do not undergo chemical reactions are drying, evaporation, dilution of solutions, distillation, extraction, and so on. These can be solved by setting up material balances containing unknowns and solving these equations for the unknowns.
In Example 1.5-1, only one unit or separate process was involved. Often, a number of processes in series are involved. Then, we have a choice of making a separate balance over each separate process and/or a balance around the complete overall process.
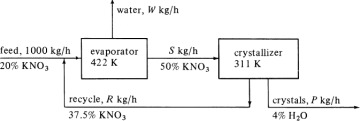
1.5C Material Balances and Recycle
Processes that have a recycle or feedback of part of the product into the entering feed are sometimes encountered. For example, in a sewage treatment plant, part of the activated sludge from a sedimentation tank is recycled back to the aeration tank where the liquid is treated. In some food-drying operations, the humidity of the entering air is controlled by recirculating part of the hot, wet air that leaves the dryer. In chemical reactions, the material that did not react in the reactor can be separated from the final product and fed back to the reactor.
1.5D Material Balances and Chemical Reaction
In many cases, the materials entering a process undergo chemical reactions in the process, so that the materials leaving are different from those entering. In these cases, it is usually convenient to make a molar and not a weight balance on an individual component, such as kg mol H2 or kg atom H, kg mol 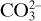 ion, kg mol CaCO3, kg atom Na+, kg mol N2, and so on. For example, in the combustion of CH4 with air, balances can be made on kg mol of H2, C, O2, or N2.
ion, kg mol CaCO3, kg atom Na+, kg mol N2, and so on. For example, in the combustion of CH4 with air, balances can be made on kg mol of H2, C, O2, or N2.
In chemical reactions with several reactants, the limiting reactant component is defined as that compound that is present in an amount less than the amount necessary for it to react stoichiometrically with the other reactants. Then, the percent completion of a reaction is the amount of this limiting reactant actually converted, divided by the amount originally present, times 100.
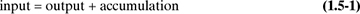


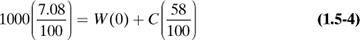
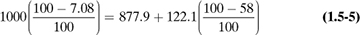
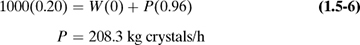

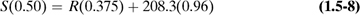


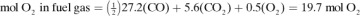
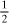 mol O2 for 1 mol H2, or 3.1
mol O2 for 1 mol H2, or 3.1 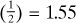 total mol O2. For completely burning the CO from Eq. (1.5-9), we need
total mol O2. For completely burning the CO from Eq. (1.5-9), we need 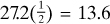 mol O2. Hence, the amount of O2 we must add is, theoretically, as follows:
mol O2. Hence, the amount of O2 we must add is, theoretically, as follows: