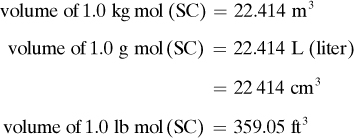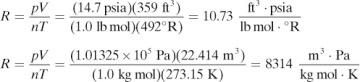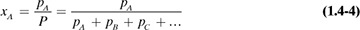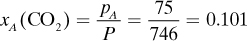- 1.0 Chapter Objectives
- 1.1 Classification of Transport Processes and Separation Processes (Unit Operations)
- 1.2 SI System of Basic Units Used in This Text and Other Systems
- 1.3 Methods of Expressing Temperatures and Compositions
- 1.4 Gas Laws and Vapor Pressure
- 1.5 Conservation of Mass and Material Balances
- 1.6 Energy and Heat Units
- 1.7 Conservation of Energy and Heat Balances
- 1.8 Numerical Methods for Integration
- 1.9 Chapter Summary
- Problems
- References
- Notation
This chapter is from the book
This chapter is from the book
This chapter is from the book
1.4 Gas Laws and Vapor Pressure
1.4A Pressure
There are numerous ways of expressing the pressure exerted by a fluid or system. An absolute pressure of 1.00 atm is equivalent to 760 mmHg at 0°C, 29.921 in. Hg, 0.760 m Hg, 14.696 lb force per square inch (psia), or 33.90 ft of water at 4°C. Gage pressure is the pressure above the absolute pressure. Hence, a pressure of 21.5 lb per square inch gage (psig) is 21.5 + 14.7 (rounded off), or 36.2 psia. In SI units, 1 psia = 6.89476 × 103 pascal (Pa) = 6.89476 × 103 newtons/m2. Also, 1 atm = 1.01325 × 105 Pa.
In some cases, particularly in evaporation, one may express the pressure as inches of mercury vacuum. This means the pressure as inches of mercury measured “below” the absolute barometric pressure. For example, a reading of 25.4 in. Hg vacuum is 29.92 – 25.4, or 4.52 in. Hg absolute pressure. Pressure conversion units are given in Appendix A.1.
1.4B Ideal Gas Law
An ideal gas is defined as one that obeys simple laws. Also, in the ideal gas approximation, the gas molecules are considered as rigid spheres that occupy no volume and do not exert forces on one another. No real gases obey these laws exactly, but at ordinary temperatures and pressures of not more than several atmospheres, the ideal gas law gives answers within a few percent or less of the actual answers. Hence, for certain situations, this law is sufficiently accurate for engineering calculations.
The ideal gas law of Boyle states that the volume of a gas is directly proportional to the absolute temperature and inversely proportional to the absolute pressure. This is expressed as
)
where p is the absolute pressure in N/m2, V is the volume of the gas in m3, n is the kg mol of the gas, T is the absolute temperature in K, and R is the gas-law constant of 8314.3 kg · m2/kg mol · s2 · K. When the volume is in ft3, n in lb moles, and T in °R, R has a value of 0.7302 ft3 · atm/lb mol · °R. For cgs units (see Appendix A.1), V = cm3, T = K, R = 82.057 cm3 · atm/g mol · K, and n = g mol.
In order that amounts of various gases may be compared, standard conditions of temperature and pressure (abbreviated STP or SC) are arbitrarily defined as 101.325 kPa (1.0 atm) abs and 273.15 K (0°C). Under these conditions, the volumes are as follows:
EXAMPLE 1.4-1. Gas-Law Constant
Calculate the value of the gas-law constant R when the pressure is in psia, moles in lb mol, volume in ft3, and temperature in °R. Repeat for SI units.
Solution: At standard conditions, p = 14.7 psia, V = 359 ft3, and T = 460 + 32 = 492°R (273.15 K). Substituting into Eq. (1.4-1) for n = 1.0 lb mol and solving for R,
)
A useful relation can be obtained from Eq. (1.4-1) for n moles of gas at conditions p1, V1, T1, and also at conditions p2, V2, T2. Substituting into Eq. (1.4-1),
p1V1 = nRT1
p2V2 = nRT2
Combining gives
)
1.4C Ideal Gas Mixtures
Dalton’s law for mixtures of ideal gases states that the total pressure of a gas mixture is equal to the sum of the individual partial pressures:
)
where P is total pressure and pA, pB, pC, ... are the partial pressures of the components A, B, C, ... in the mixture.
Since the number of moles of a component is proportional to its partial pressure, the mole fraction of a component is
)
The volume fraction is equal to the mole fraction. Gas mixtures are almost always represented in terms of mole fractions and not weight fractions. For engineering purposes, Dalton’s law is sufficiently accurate to use for actual mixtures at total pressures of a few atmospheres or less.
EXAMPLE 1.4-2. Composition of a Gas Mixture
A gas mixture contains the following components and partial pressures: CO2, 75 mmHg; CO, 50 mmHg; N2, 595 mmHg; and O2, 26 mmHg. Calculate the total pressure and the composition in mole fraction.
Solution: Substituting into Eq. (1.4-3),
P = pA + pB + pC + pD = 75 + 50 + 595 + 26 = 746 mmHg
The mole fraction of CO2 is obtained by using Eq. (1.4-4).
In like manner, the mole fractions of CO, N2, and O2 are calculated as 0.067, 0.797, and 0.035, respectively.
1.4D Vapor Pressure and Boiling Point of Liquids
When a liquid is placed in a sealed container, molecules of the liquid will evaporate into the space above the liquid and fill it completely. After a fixed amount of time, equilibrium is reached. This vapor will exert a pressure just like a gas and we call this pressure the vapor pressure of the liquid. The value of the vapor pressure is independent of the amount of liquid in the container as long as some is present.
If an inert gas such as air is also present in the vapor space, it will have very little effect on the vapor pressure. In general, the effect of total pressure on vapor pressure can be considered as negligible for pressures of a few atmospheres or less.
The vapor pressure of a liquid increases markedly with temperature. For example, from Appendix A.2 for water, the vapor pressure at 50°C is 12.333 kPa (92.51 mmHg). At 100°C, the vapor pressure has increased greatly to 101.325 kPa (760 mmHg).
The boiling point of a liquid is defined as the temperature at which the vapor pressure of a liquid equals the total pressure. Hence, if the atmospheric total pressure is 760 mmHg, water will boil at 100°C. On top of a high mountain, where the total pressure is considerably less, water will boil at temperatures below 100°C.
A plot of vapor pressure PA of a liquid versus temperature does not yield a straight line but a curve. However, for moderate temperature ranges, a plot of log PA versus 1/T is a reasonably straight line, as follows:
)
where m is the slope, b is a constant for the liquid A, and T is the temperature in K.