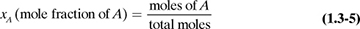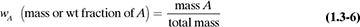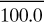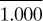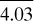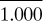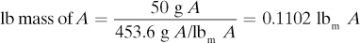- 1.0 Chapter Objectives
- 1.1 Classification of Transport Processes and Separation Processes (Unit Operations)
- 1.2 SI System of Basic Units Used in This Text and Other Systems
- 1.3 Methods of Expressing Temperatures and Compositions
- 1.4 Gas Laws and Vapor Pressure
- 1.5 Conservation of Mass and Material Balances
- 1.6 Energy and Heat Units
- 1.7 Conservation of Energy and Heat Balances
- 1.8 Numerical Methods for Integration
- 1.9 Chapter Summary
- Problems
- References
- Notation
This chapter is from the book
This chapter is from the book
This chapter is from the book
1.3 Methods of Expressing Temperatures and Compositions
1.3A Temperature
There are two temperature scales in common use in the chemical and biological industries. These are degrees Fahrenheit (abbreviated °F) and Celsius (°C). It is often necessary to convert from one scale to the other. Both use the freezing point and boiling point of water at 1 atmosphere pressure as base points. Temperatures are often expressed as absolute degrees K (SI standard) or degrees Rankine (°R) instead of °C or °F. Table 1.3-1 shows the equivalences of the four temperature scales.
The difference between the boiling point of water and melting point of ice at 1 atm is 100°C or 180°F. Thus, a 1.8°F change is equal to a 1°C change. Usually, the value of –273.15°C is rounded to –273.2°C and –459.67°F to –460°F. The following equations can be used to convert from one temperature scale to another:
)
)
)
)
1.3B Mole Units and Weight or Mass Units
There are many methods used to express compositions in gases, liquids, and solids. One of the most useful is molar units, since chemical reactions and gas laws are simpler to express in terms of molar units. A mole (mol) of a pure substance is defined as the amount of that substance whose mass is numerically equal to its molecular weight. Hence, 1 kg mol of methane CH4 contains 16.04 kg. Also, 1.0 lb mol of methane contains 16.04 lbm.
The mole fraction of a particular substance is simply the moles of this substance divided by the total number of moles. Likewise, the weight or mass fraction is the mass of the substance divided by the total mass. These two compositions, which hold for gases, liquids, and solids, can be expressed as follows for component A in a mixture:
)
)
Table 1.3-1. Temperature Scales and Equivalents
|
Centigrade |
Fahrenheit |
Kelvin |
Rankine |
Celsius |
|---|---|---|---|---|---|
Boiling water |
100°C |
212°F |
373.15 K |
671.67°R |
100°C |
Melting ice |
0°C |
32°F |
273.15 K |
491.67°R |
0°C |
Absolute zero |
–273.15°C |
–459.67°F |
0 K |
0°R |
–273.15°C |
EXAMPLE 1.3-1. Mole and Mass, or Weight Fraction of a Solution
A container holds 50 g of water (B) and 50 g of NaOH (A). Calculate the weight fraction and mole fraction of NaOH. Also, calculate the lbm of NaOH (A) and H2O (B).
Solution: Taking as a basis for calculation 50 + 50 or 100 g of solution, the following data are calculated:
Component |
G |
Wt Fraction |
Mol Wt |
G Moles |
Mole Fraction |
|---|---|---|---|---|---|
H2O (B) |
50.0 |
|
18.02 |
|
|
NaOH (A) |
50.0 |
|
40.0 |
|
|
Total |
|
|
|
|
Hence, xA = 0.310, xB = 0.690, and xA + xB = 0.310 + 0.690 = 1.00. Also, wA + wB = 0.500 + 0.500 = 1.00. To calculate the lbm of each component, Appendix A.1 gives the conversion factor of 453.6 g per 1 lbm. Using this,
)
Note that the g of A in the numerator cancels the g of A in the denominator, leaving lbm of A in the numerator of the final answer. The reader is cautioned to put all units down in an equation and cancel those appearing in the numerator and denominator. In a similar manner, we obtain 0.1102 lbm B (0.0500 kg B).
The analyses of solids and liquids are usually given as a weight or mass fraction or a weight percent, and gases as a mole fraction or percent. Unless otherwise stated, analyses of solids and liquids will be assumed to be a weight (mass) fraction or percent, and those of gases to be a mole fraction or percent.
1.3C Concentration Units for Liquids
In general, when one liquid is mixed with another miscible liquid, the volumes are not additive. Hence, compositions of liquids are usually not expressed as the volume percent of a component but as the weight or mole percent. Another convenient way to express concentrations of components in a solution is molarity, which is defined as g mol of a component per liter of solution. Other methods used are kg/m3, g/liter, g/cm3, lb mol/ft3, lbm/ft3, and lbm/gallon. All of these concentrations depend on temperature, so the temperature must be specified.
The most common method of expressing total concentration per unit volume is density, kg/m3, g/cm3, or lbm/ft3. For example, the density of water at 277.2 K (4°C) is 1000 kg/m3, or 62.43 lbm/ft3. Sometimes the density of a solution is expressed as specific gravity, which is defined as the density of the solution at its given temperature divided by the density of a reference substance at its temperature. If the reference substance is water at 277.2 K, the specific gravity and density of the substance are numerically equal.