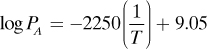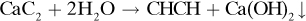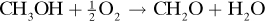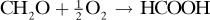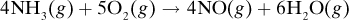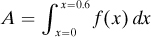Introduction to Engineering Principles and Units

This chapter is from the book

Transport Processes and Separation Process Principles, 5th Edition

Learn More Buy

This chapter is from the book

This chapter is from the book 

Transport Processes and Separation Process Principles, 5th Edition

Learn More Buy

Problems

1.2-1. Temperature of a Chemical Process. The temperature of a chemical reaction was found to be 353.2 K. What is the temperature in °F, °C, and °R?

Ans. 176°F, 80°C, 636°R

1.2-2. Temperature for Smokehouse Processing of Meat. In smokehouse processing of sausage meat, a final temperature of 155°F inside the sausage is often used. Calculate this temperature in °C, K, and °R.

1.3-1. Molecular Weight of Air. For purposes of most engineering calculations, air is assumed to be composed of 21 mol % oxygen and 79 mol % nitrogen. Calculate the average molecular weight.

Ans. 28.9 g mass/g mol, lb mass/lb mol, or kg mass/kg mol

1.3-2. Oxidation of CO and Mole Units. The gas CO is being oxidized by O₂ to form CO₂. How many kg of CO₂ will be formed from 56 kg of CO? Also, calculate the kg of O₂ theoretically needed for this reaction. (Hint: First, write the balanced chemical equation to obtain the mol O₂ needed for 1.0 kg mol CO. Then, calculate the kg mol of CO in 56 kg CO.)

Ans. 88.0 kg CO₂, 32.0 kg O₂

1.3-3. Composition of a Gas Mixture. A gaseous mixture contains 20 g of N₂, 83 g of O₂, and 45 g of CO₂. Calculate the composition in mole fraction and the average molecular weight of the mixture.

Ans. Average mol wt = 34.2 g mass/g mol, 34.2 kg mass/kg mol

1.3-4. Composition of a Protein Solution. A liquid solution contains 1.15 wt % of a protein, 0.27 wt % KCl, and the remainder is water. The average molecular weight of the protein by gel permeation is 525000 g mass/g mol. Calculate the mole fraction of each component in solution.

1.3-5. Concentration of NaCl Solution. An aqueous solution of NaCl has a concentration of 24.0 wt % NaCl with a density of 1.178 g/cm³ at 25°C. Calculate the following:

1. Mole fraction of NaCl and water.

2. Concentration of NaCl as g mol/liter, lb_m/ft³, lb_m/gal, and kg/m³.

1.4-1. Conversion of Pressure Measurements in Freeze Drying. In the experimental measurement of freeze drying of beef, an absolute pressure of 2.4 mmHg was held in the chamber. Convert this pressure to atm, in. of water at 4°C, μm of Hg, and Pa. (Hint: See Appendix A.1 for conversion factors.)

Ans. 3.16 × 10^–3 atm, 1.285 in. H₂O, 2400 μm Hg, 320 Pa

1.4-2. Compression and Cooling of Nitrogen Gas. A volume of 65.0 ft³ of N₂ gas at 90°F and 29.0 psig is compressed to 75 psig and cooled to 65°F. Calculate the final volume in ft³ and the final density in lb_m/ft³. [Hint: Be sure to convert all pressures to psia first and then to atm. Substitute original conditions into Eq. (1.4-1) to obtain n, lb mol.]

1.4-3. Gas Composition and Volume. A gas mixture of 0.13 g mol NH₃, 1.27 g mol N₂, and 0.025 g mol H₂O vapor is contained at a total pressure of 830 mmHg and 323 K. Calculate the following:.

1. Mole fraction of each component.

2. Partial pressure of each component in mmHg.

3. Total volume of mixture in m³ and ft³.

1.4-4. Evaporation of a Heat-Sensitive Organic Liquid. An organic liquid is being evaporated from a liquid solution containing a few percent nonvolatile dissolved solids. Since it is heat-sensitive and may discolor at high temperatures, it will be evaporated under vacuum. If the lowest absolute pressure that can be obtained in the apparatus is 12.0 mmHg, what will be the temperature of evaporation in K? It will be assumed that the small amount of solids does not affect the vapor pressure, which is given as follows:

where P_A is in mmHg and T in K.

Ans. T = 282.3 K or 9.1°C

1.5-1. Evaporation of Cane Sugar Solutions. An evaporator is used to concentrate cane sugar solutions. A feed of 10000 kg/d of a solution containing 38 wt % sugar is evaporated, producing a 74 wt % solution. Calculate the weight of solution produced and the amount of water removed.

Ans. 5135 kg/d of 74 wt % solution, 4865 kg/d water

1.5-2. Processing of Fish Meal. Fish are processed into fish meal and used as a supplementary protein food. In the processing, the oil is first extracted to produce a wet fish cake containing 80 wt % water and 20 wt % bone-dry cake. This wet cake feed is dried in rotary-drum dryers to give a “dry” fish cake product containing 40 wt % water. Finally, the product is finely ground and packed. Calculate the kg/h of wet cake feed needed to produce 1000 kg/h of “dry” fish cake product.

Ans. 3000 kg/h wet cake feed

1.5-3. Drying of Lumber. A batch of 100 kg of wet lumber containing 11 wt % moisture is dried to a water content of 6.38 kg water/1.0 kg bone-dry lumber. What is the weight of “dried” lumber and the amount of water removed?

1.5-4. Processing of Paper Pulp. A wet paper pulp contains 68 wt % water. After the pulp was dried, it was found that 55% of the original water in the wet pulp was removed. Calculate the composition of the “dried” pulp and its weight for a feed of 1000 kg/min of wet pulp.

1.5-5. Two-Stage Production of Jam from Crushed Fruit. In a process producing jam, crushed fruit containing 14 wt % soluble solids is combined with sugar (1.22 kg sugar/1.00 kg crushed fruit) and pectin (0.0025 kg pectin/1.00 kg crushed fruit) in a mixer. The resultant mixture is then evaporated in a kettle to produce a jam containing 67 wt % soluble solids. For a feed of 1000 kg crushed fruit, calculate the kg mixture from the mixer, kg water evaporated, and kg jam produced.

Ans. 2222.5 kg mixture, 189 kg water, 2033.5 kg jam

1.5-6. Drying of Cassava (Tapioca) Root. Tapioca flour is used in many countries for bread and similar products. The flour is made by drying coarse granules of the cassava root containing 66 wt % moisture to 5% moisture and then grinding to produce the flour. How many kg of granules must be dried and how much water removed to produce 5000 kg/h of flour?

1.5-7. Processing of Soybeans in Three Stages. A feed of 10000 kg of soybeans is processed in a sequence of three stages or steps (E1). The feed contains 35 wt % protein, 27.1 wt % carbohydrate, 9.4 wt % fiber and ash, 10.5 wt % moisture, and 18.0 wt % oil. In the first stage, the beans are crushed and pressed to remove oil, giving an expressed-oil stream and a stream of pressed beans containing 6% oil. Assume no loss of other constituents with the oil stream. In the second step, the pressed beans are extracted with hexane to produce an extracted-meal stream containing 0.5 wt % oil and a hexane–oil stream. Assume no hexane in the extracted meal. Finally, in the last step the extracted meal is dried to give a dried meal of 8 wt % moisture. Calculate the following:

1. kg of pressed beans from the first stage.

2. kg of extracted meal from the second stage.

3. kg of final dried meal and the wt % protein in the dried meal.

Ans. (a) 8723 kg; (b) 8241 kg; (c) 7816 kg, 44.8 wt % protein

1.5-8. Recycle in a Dryer. A solid material containing 15.0 wt % moisture is dried so that it contains 7.0 wt % water by blowing fresh warm air mixed with recycled air over the solid in the dryer. The inlet fresh air has a humidity of 0.01 kg water/kg dry air, the air from the drier that is recycled has a humidity of 0.1 kg water/kg dry air, and the mixed air to the dryer, 0.03 kg water/kg dry air. For a feed of 100 kg solid/h fed to the dryer, calculate the kg dry air/h in the fresh air, the kg dry air/h in the recycled air, and the kg/h of “dried” product.

Ans. 95.6 kg/h dry air in fresh air, 27.3 kg/h dry air in recycled air, and 91.4 kg/h “dried” product

1.5-9. Crystallization and Recycle. It is desired to produce 1000 kg/h of Na₃PO₄ · 12H₂O crystals from a feed solution containing 5.6 wt % Na₃PO₄ and traces of impurity. The original solution is first evaporated in an evaporator to a 35 wt % Na₃PO₄ solution and then cooled to 293 K in a crystallizer, where the hydrated crystals and a mother-liquor solution are removed. One out of every 10 kg of mother liquor is discarded to waste to get rid of the impurities, and the remaining mother liquor is recycled to the evaporator. The solubility of Na₃PO₄ at 293 K is 9.91 wt %. Calculate the kg/h of feed solution and kg/h of water evaporated.

Ans. 7771 kg/h feed, 6739 kg/h water

1.5-10. Evaporation and Bypass in an Orange Juice Concentration. In a process for concentrating 1000 kg of freshly extracted orange juice (C1) containing 12.5 wt % solids, the juice is strained, yielding 800 kg of strained juice and 200 kg of pulpy juice. The strained juice is concentrated in a vacuum evaporator to give an evaporated juice of 58% solids. The 200 kg of pulpy juice is bypassed around the evaporator and mixed with the evaporated juice in a mixer to improve the flavor. This final concentrated juice contains 42 wt % solids. Calculate the concentration of solids in the strained juice, the kg of final concentrated juice, and the concentration of solids in the pulpy juice bypassed. (Hint: First, make a total balance and then a solids balance on the overall process. Next, make a balance on the evaporator. Finally, make a balance on the mixer.)

Ans. 34.2 wt % solids in pulpy juice

1.5-11. Manufacture of Acetylene. To make 6000 ft³ of acetylene (CHCH) gas at 70°F and 750 mmHg, solid calcium carbide (CaC₂), which contains 97 wt % CaC₂ and 3 wt % solid inerts, is used along with water. The reaction is

The final lime slurry contains water, solid inerts, and Ca(OH)₂ lime. In this slurry, the total wt % solids of inerts plus Ca(OH)₂ is 20%. How many lb of water must be added and how many lb of final lime slurry is produced? [Hint: Use a basis of 6000 ft³ and convert to lb mol. This gives 15.30 lb mol C₂H₂, 15.30 lb mol Ca(OH)₂, and 15.30 lb mol CaC₂ added. Convert lb mol CaC₂ feed to lb and calculate lb inerts added. The total lb solids in the slurry is then the sum of the Ca(OH)₂ plus inerts. In calculating the water added, remember that some is consumed in the reaction.]

Ans. 5200 lb water added (2359 kg), 5815 lb lime slurry (2638 kg)

1.5-12. Combustion of Solid Fuel. A fuel analyzes 74.0 wt % C and 12.0% ash (inert). Air is added to burn the fuel, producing a flue gas of 12.4% CO₂, 1.2% CO, 5.7% O₂, and 80.7% N₂. Calculate the kg of fuel used for 100 kg mol of outlet flue gas and the kg mol of air used. (Hint: First, calculate the mol O₂ added in the air, using the fact that the N₂in the flue gas equals the N₂ added in the air. Then, make a carbon balance to obtain the total moles of C added.)

1.5-13. Burning of Coke. A furnace burns a coke containing 81.0 wt % C, 0.8% H, and the rest inert ash. The furnace uses 60% excess air (air over and above that needed to burn all C to CO₂and H to H₂O). Calculate the moles of all components in the flue gas if only 95% of the carbon goes to CO₂and 5% to CO.

1.5-14. Production of Formaldehyde. Formaldehyde (CH₂O) is made by the catalytic oxidation of pure methanol vapor and air in a reactor. The moles from this reactor are 63.1 N₂, 13.4 O₂, 5.9 H₂O, 4.1 CH₂O, 12.3 CH₃OH, and 1.2 HCOOH. The reaction is

A side reaction occurring is

Calculate the mol methanol feed, mol air feed, and percent conversion of methanol to formaldehyde.

Ans. 17.6 mol CH₃OH, 79.8 mol air, 23.3% conversion

1.6-1. Heating of CO₂ Gas. A total of 250 g of CO₂ gas at 373 K is heated to 623 K at 101.32 kPa total pressure. Calculate the amount of heat needed in cal, btu, and kJ.

Ans. 15050 cal, 59.7 btu, 62.98 kJ

1.6-2. Heating a Gas Mixture. A mixture of 25 lb mol N₂ and 75 lb mol CH₄ is being heated from 400°F to 800°F at 1 atm pressure. Calculate the total amount of heat needed in btu.

1.6-3. Final Temperature in Heating Applesauce. A mixture of 454 kg of applesauce at 10°C is heated in a heat exchanger by adding 121300 kJ. Calculate the outlet temperature of the applesauce. (Hint: In Appendix A.4, a heat capacity for applesauce is given at 32.8°C. Assume that this is constant and use this as the average c_pm.)

Ans. 76.5°C

1.6-4. Use of Steam Tables. Using the steam tables, determine the enthalpy change for 1 lb water for each of the following cases:

1. Heating liquid water from 40°F to 240°F at 30 psia. (Note: The effect of total pressure on the enthalpy of liquid water can be neglected.)

2. Heating liquid water from 40°F to 240°F and vaporizing at 240°F and 24.97 psia.

3. Cooling and condensing a saturated vapor at 212°F and 1 atm abs to a liquid at 60°F.

4. Condensing a saturated vapor at 212°F and 1 atm abs.

Ans. (a) 200.42 btu/lb_m; (b) 1152.7 btu/lb_m; (c) –1122.4 btu/lb_m; (d) –970.3 btu/lb_m, –2256.9 kJ/kg

1.6-5. Heating and Vaporization Using Steam Tables. A flow rate of 1000 kg/h of water at 21.1°C is heated to 110°C when the total pressure is 244.2 kPa in the first stage of a process. In the second stage at the same pressure, the water is heated further, until it is all vaporized at its boiling point. Calculate the total enthalpy change in the first stage and in both stages.

1.6-6. Combustion of CH₄ and H₂. For 100 g mol of a gas mixture of 75 mol % CH₄ and 25% H₂, calculate the total heat of combustion of the mixture at 298 K and 101.32 kPa, assuming that combustion is complete.

1.6-7. Heat of Reaction from Heats of Formation. For the reaction

calculate the heat of reaction, ΔH, at 298 K and 101.32 kPa for 4 g mol of NH₃ reacting.

Ans. ΔH, heat of reaction = –904.7 kJ

1.7-1. Heat Balance and Cooling of Milk. In the processing of rich cows’ milk, 4540 kg/h of milk is cooled from 60°C to 4.44°C by a refrigerant. Calculate the heat removed from the milk.

Ans. Heat removed = 269.6 kW

1.7-2. Heating of Oil by Air. A flow of 2200 lb_m/h of hydrocarbon oil at 100°F enters a heat exchanger, where it is heated to 150°F by hot air. The hot air enters at 300°F and is to leave at 200°F. Calculate the total lb mol air/h needed. The mean heat capacity of the oil is 0.45 btu/lb_m · °F.

Ans. 70.1 lb mol air/h, 31.8 kg mol/h

1.7-3. Combustion of Methane in a Furnace. A gas stream of 10 000 kg mol/h of CH₄ at 101.32 kPa and 373 K is burned in a furnace using air at 313 K. The combustion is complete and 50% excess air is used. The flue gas leaves the furnace at 673 K. Calculate the heat removed in the furnace. (Hint: Use a datum of 298 K and liquid water at 298 K. The input items will be the following: the enthalpy of CH₄ at 373 K referred to 298 K; the enthalpy of the air at 313 K referred to 298 K; – 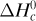, the heat of combustion of CH₄ at 298 K, which is referred to liquid water; and q, the heat added. The output items will include: the enthalpies of CO₂, O₂, N₂, and H₂O gases at 673 K referred to 298 K; and the latent heat of H₂O vapor at 298 K and 101.32 kPa from Appendix A.2. It is necessary to include this latent heat since the basis of the calculation and of the 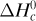, is liquid water.)

1.7-4. Preheating Air by Steam for Use in a Dryer. An air stream at 32.2°C is to be used in a dryer and is first preheated in a steam heater to 65.5°C. The air flow is 1000 kg mol/h. The steam enters the heater saturated at 148.9°C, is condensed and cooled, and leaves as a liquid at 137.8°C. Calculate the amount of steam used in kg/h.

Ans. 450 kg steam/h

1.7-5. Cooling Cans of Potato Soup After Thermal Processing. A total of 1500 cans of potato soup undergo thermal processing in a retort at 240°F. Before being removed from the retort, the cans are then cooled to 100°F by cooling water, which enters at 75°F and leaves at 85°F. Calculate the lb of cooling water needed. Each can of soup contains 1.0 lb of liquid soup, and the empty metal can weighs 0.16 lb. The mean heat capacity of the soup is 0.94 btu/lb_m · °F and that of the metal can is 0.12 btu/lb_m · °F. A metal rack or basket which is used to hold the cans in the retort weighs 350 lb and has a heat capacity of 0.12 btu/lb_m · °F. Assume that the metal rack is cooled from 240°F to 85°F, the temperature of the outlet water. The amount of heat removed from the retort walls in cooling from 240 to 100°F is 10 000 btu. Radiation loss from the retort during cooling is estimated as 5000 btu.

Ans. 21320 lb water, 9670 kg

1.8-1. Numerical Integration Using Simpson’s Method. The following experimental data for y = f(x) were obtained:

Determine the integral using Simpson’s method:

Ans. A = 38.45

1.8-2. Numerical Integration to Obtain Wastewater Flow. The rate of flow of wastewater in an open channel has been measured and the following data obtained:

Determine the total flow in m³ for 120 min by numerical integration.

Ans. 92 350 m³