- 5.1 Frequency-Flat Wireless Channels
- 5.2 Equalization of Frequency-Selective Channels
- 5.3 Estimating Frequency-Selective Channels
- 5.4 Carrier Frequency Offset Correction in Frequency-Selective Channels
- 5.5 Introduction to Wireless Propagation
- 5.6 Large-Scale Channel Models
- 5.7 Small-Scale Fading Selectivity
- 5.8 Small-Scale Channel Models
- 5.9 Summary
- Problems
This chapter is from the book
This chapter is from the book
This chapter is from the book
5.7 Small-Scale Fading Selectivity
In this section, we discuss small-scale fading effects. These effects, which occur on the order of a wavelength distance, are caused by the constructive and destructive interference of multipath components. These effects manifest in the time domain, leading to time selectivity or, in the frequency domain, leading to frequency selectivity. These two forms of selectivity are independent of each other, under some assumptions. Before proceeding with the mathematical details, we first develop the intuition behind time- and frequency-selective channels. Then we present the foundations for determining whether a channel is frequency selective or time selective. We conclude with showing the potential system models used in each fading regime.
5.7.1 Introduction to Selectivity
In this section, we introduce frequency selectivity and time selectivity. We pursue these in further detail in subsequent sections.
Frequency selectivity refers to the variation of the channel amplitude with respect to frequency. To understand how multipath plays an important role in frequency selectivity, consider the following two examples. Figure 5.32(a) illustrates the frequency response with a single channel tap. In the frequency domain, the Fourier transform of the single impulse function yields a flat channel; that is, the channel amplitude does not vary with frequency. We explored the flat channel in Section 5.1. Alternatively, in Figure 5.32(b), the channel impulse response has a significant amount of multipath. In the frequency domain (taking the Fourier transform of the sum of shifted impulse functions), the resultant channel varies considerably with frequency.
){kind=link}
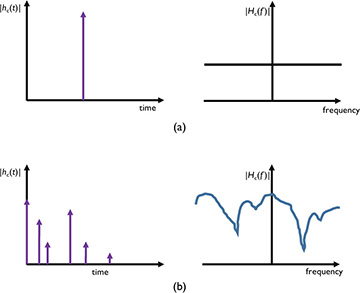
Figure 5.32 A single path channel (a) and a multipath channel (b). The single path has a frequency-flat response whereas the multipath channel has a frequency-selective response.
The effect of frequency selectivity, though, depends critically on the bandwidth used to communicate in that channel. For example, illustrated in Figure 5.33 are the discrete-time complex baseband equivalent channels for two different choices of bandwidth, 1MHz and 10MHz. With the smaller bandwidth, the impulse response looks nearly like a discrete-time delta function, corresponding to a flat channel. With the larger bandwidth, there are more taps (since the symbol period is smaller) and there are many more significant taps, leading to substantial intersymbol interference. Therefore, the same channel can appear frequency flat or frequency selective depending on the signal bandwidth. The range of frequencies over which the channel amplitude remains fairly constant is the coherence bandwidth.
){kind=link}
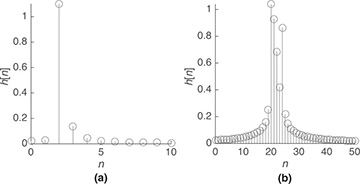
Figure 5.33 (a) Discrete-time complex baseband equivalent channel for a five-path channel with a narrow bandwidth; (b) discrete-time complex baseband equivalent channel for a five-path channel with a bandwidth ten times larger
Time selectivity refers to the variation in the channel amplitude as a function of time. The degree or extent of time selectivity of a channel is measured using the coherence time of the channel. This simply refers to the time duration over which the channel remains fairly constant. The coherence time provides guidance on when the received signal model can be assumed to be LTI. Time selectivity is a function of the mobility present in the channel and is usually measured using the Doppler spread or the maximum Doppler shift.
For the coherence time to be useful, it must be compared with some property of the signal. For example, suppose that the receiver processes data in packets of length Ntot. For the LTI assumption to be valid, the channel should be roughly constant during the entire packet. Then, if TNtot is less than the coherence time, we might say that the LTI assumption is good and the channel is time invariant or slow fading. This does not mean that the channel does not vary at all; rather it means that during the window of interest (in this case Ntot symbols with period T) the channel can be considered to be time invariant. If TNtot is greater than the coherence time, then we might say that the LTI assumption is not good and that the channel is time selective or fast fading.
Note that the bandwidth also plays a role in determining the coherence time of a signal. Assuming a sinc pulse-shaping filter, the symbol period T = 1/B. As a result, making the bandwidth larger reduces the duration of the Ntot symbols. Of course, increasing the bandwidth makes it more likely that the channel is frequency selective. This shows how the time and frequency variability of a channel are intertwined.
The time and frequency selectivity are coupled together. For example, if the receiver is moving and the multipaths come from different directions, each has a different Doppler shift. As a result, the time variability with several multipaths is more severe than with a single multipath. Fortunately, making some statistical assumptions about the channel allows the time selectivity to be decoupled from the frequency selectivity. Specifically, if the channel is assumed to satisfy the wide-sense stationary uncorrelated scattering assumption (WSSUS) [33], then the time-selective and frequency-selective parts of the correlation function can be decoupled, and the decision about a channel’s selectivity can be made separately based on certain correlation functions, discussed in the next sections. Quantities computed from these correlation functions are compared with the bandwidth of the signal of interest, the symbol period, and the block length Ntot to determine the effective selectivity.
To explain this mathematically, suppose that the continuous-time complex baseband equivalent channel impulse response is h(t, τ) where t is the time and τ is the lag. This is a doubly selective channel, in that it varies both with time and with lag. The channel is measured assuming a large bandwidth, typically larger than the eventual bandwidth of the signal that will be used in this channel. For example, measurements might be made in a 500MHz channel and the results of those measurements used to decide how to partition the bandwidth among different signals. We use continuous time as this is historically how the WSSUS description was developed [33], but interpretations are also available in discrete time [152, 301].
Under the WSSUS model, a statistical description of the channel correlations is made through two functions: the power delay profile Rdelay(τ), and the Doppler spectrum SDoppler(f). The power delay profile gives a measure of how the energy of the channel varies in the lag domain for two signals of very short duration (so Doppler is neglected). The Doppler spectrum measures essentially how much power is present in different Doppler shifts of two narrowband signals (so lag is neglected). Frequency selectivity is decided based on Rdelay(τ), and time selectivity is decided based on SDoppler(f). In the next sections, we explore further the idea of determining the selectivity of a channel based on the power delay profile and the Doppler spectrum, or their Fourier transforms.
5.7.2 Frequency-Selective Fading
We use the power delay profile Rdelay(τ) to determine whether a channel is frequency-selective fading. The power delay profile is typically determined from measurements; common power delay profiles can be found in different textbooks and in many standards. For example, the GSM standard specifies several different profiles, including parameters like typical urban, rural, bad urban, and others. Intuitively, in a flat channel (in the bandwidth where the power delay profile was measured) Rdelay(τ) should be close to a delta function.
The typical way to measure the severity of a power delay profile is based on the root mean square (RMS) delay spread. Define the mean excess delay as
and the second moment as
Then the RMS delay spread is the difference:
With this definition, a channel is said to be frequency flat if the symbol period satisfies T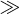 
σRMS,delay. This means that the effective spread is much smaller than a symbol, so there will be little ISI between adjacent symbols.
Example 5.30 Consider the exponential power delay profile Rdelay(τ) = e−τ/γ. Determine the RMS delay spread.
Answer: The mean excess delay is
The second moment is
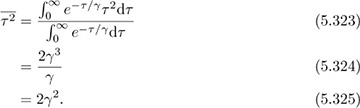
Therefore, the RMS delay spread is
Therefore, the value γ is the RMS delay spread.
The Fourier transform of the power delay profile is known as the spaced-frequency correlation function:
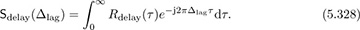
It measures the correlation as a function of the difference Δlag = f2−f1 between sinusoids sent on two different carrier frequencies. The spaced-frequency correlation function is used to define the coherence bandwidth of the channel. One definition of coherence bandwidth is the smallest value of Δlag such that |Sdelay(Bcoh)| = 0.5Sdelay(0). Essentially this is the first point where the channel becomes decorrelated by 0.5.
It is common to define the coherence bandwidth based on the RMS delay spread. For example,
The coherence bandwidth is interpreted like traditional bandwidth and is meant to give a measure over which the channel is (statistically speaking) reasonably flat. In particular, a channel is flat if the bandwidth B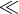 
Bcoh. There are several different definitions of coherence bandwidth in the literature; all have an inverse relationship with the RMS delay spread [191, 270].
Example 5.31 Determine the spaced-frequency correlation function, the coherence bandwidth from the spaced-frequency correlation function, and the coherence bandwidth from the RMS delay spread for the exponential power delay profile in Example 5.30.
Answer: The spaced-frequency correlation function is
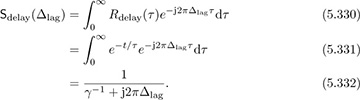
To find the coherence bandwidth from the spaced-frequency correlation function:
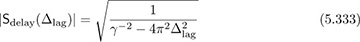
and
The smallest nonnegative value of Δlag that determines the coherence bandwidth is
Based on the RMS delay spread,
Since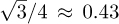 
and 1/5 = 0.2, these two expressions differ by a factor of 2. The coherence bandwidth based on the RMS delay spread is more conservative between the two measures in this case.
In practice, the power delay profile or spaced-frequency correlation function is determined from measurements. For example, suppose that a training signal is used to generate channel estimate h[n, ℓ] at time n. Then the discrete-time power delay profile can be estimated from M observations as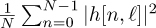 
. The spaced-frequency correlation function Sdelay(Δlag) could be estimated by sending sinusoids at Δf = f2 − f1 and estimating the correlation between their respective channels at several different times. Or it could be computed in discrete time using an OFDM system by taking the DFT of each channel estimate H[n, k] for a given n, assuming K total subcarriers, then estimating the spaced-frequency correlation as a function of subcarriers as 
.
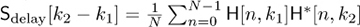5.7.3 Time-Selective Fading
The Doppler spectrum SDoppler(f) is used to determine if a channel is time-selective fading. The Doppler spectrum can be estimated via measurements or more commonly is based on certain analytical models. Given a general Doppler spectrum, a common approach for determining the severity of the Doppler is to define an RMS Doppler spread σRMS,doppler in the same way the RMS delay spread is defined. Then a signal is considered to be time invariant if B 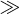σRMS,doppler. In mobile channels, the maximum Doppler shift may be used instead of the RMS Doppler spread. The maximum Doppler shift is fm = fcν/c where ν is the maximum velocity and c is the speed of light. The maximum shift occurs when the transmitter is moving either straight to or straight from the receiver with velocity ν. For many systems, the maximum Doppler shift gives a reasonable approximation of the RMS Doppler spread, typically leading to a more conservative definition of time selective.
The maximum Doppler shift varies as a function of mobility. When there is higher mobility, the velocity is higher. From a system design perspective, we often use the maximum velocity to determine the coherence time. For example, a fixed wireless system might assume only pedestrian speeds of 2mph, whereas a mobile cellular system might be designed for high-speed trains that travel at hundreds of miles per hour.
Example 5.32 Determine the maximum Doppler shift for a cellular system with fc = 1.9GHz that serves high-speed trains with a velocity of 300km/h.
Answer: The velocity of 300km/h in meters per second is 83.3m/s. The maximum Doppler shift is then
Analytical models can also be used to determine the Doppler spectrum. Perhaps the most common is the Clarke-Jakes model. In this model, the transmitter is stationary while the receiver is moving with a velocity of ν directly toward the transmitter. There is a ring of isotropic scatterers around the receiver, meaning that multipaths arrive from all different directions and with different corresponding Doppler shifts. The Doppler spectrum under this assumption is
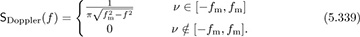
Plotting the Clarke-Jakes spectrum in Figure 5.34, we see what is known as the horned Doppler spectrum.
){kind=link}
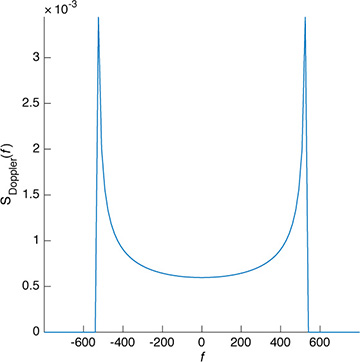
Figure 5.34 The Clarke-Jakes spectrum plotted for fm = 533Hz
The time selectivity of the channel can also be determined from the spaced-time correlation function, which is the inverse Fourier transform of the Doppler spectrum:
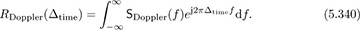
The spaced-time correlation function essentially gives the correlation between narrowband signals (so delay spread can be neglected) at two different points in time Δtime = t2 − t1. The coherence time of the channel is defined as the smallest value of Δtime such that |RDoppler(Δtime)| = 0.5RDoppler(0). The resulting value is Tcoh. It is common to define the coherence time based on either the RMS Doppler spread or the maximum Doppler shift, in the same way that the coherence bandwidth is defined. A channel is said to be LTI over block Ntot if TNtot Tcoh. For the Clarke-Jakes spectrum, it is common to take Tcoh = 0.423/fm [270].
Example 5.33 Determine the coherence time using the maximum Doppler shift for the same situation as in Example 5.32. Also, if a single-carrier system with 1MHz of bandwidth is used, and packets of length Ntot = 100 are employed, determine if the channel is time selective.
Answer: The coherence time is Tcoh = 1/(5fm) = 0.375ms. With a bandwidth of 1MHz, T is at most 1µs, assuming sinc pulse shaping, less if other forms of pulse shaping are used. Comparing NtotT = 100µs with Tcoh, we can conclude that the channel will be time invariant during the packet.
For the Clarke-Jakes spectrum, the spaced-time correlation function can be computed as
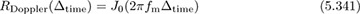
where J0(·) is the zeroth-order Bessel function. The spaced-time correlation function is plotted in Figure 5.35. The ripples in the temporal correlation function lead to rapid decorrelation but do show some longer-term correlations over time.
){kind=link}
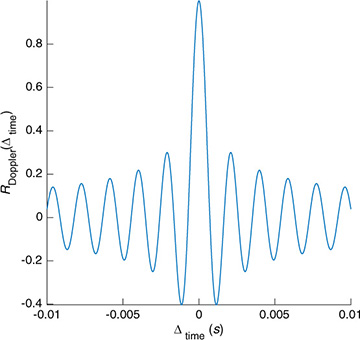
Figure 5.35 The spaced-time correlation function corresponding to the Clarke-Jakes spectrum plotted for fm = 533Hz
An interesting aspect of time-selective fading is that it depends on the carrier. Normally we use the baseband equivalent channel model and forget about the carrier fc. Here is one place where it is important. Note that the higher the carrier, the smaller the coherence time for a fixed velocity. This means that higher-frequency signals suffer more from time variations than lower-frequency signals.
In practice, it is common to determine the spaced-time correlation function from measurements. For example, suppose that short training sequences are used to generate channel h[n, ℓ] at time n over N measurements. The spaced-time correlation function may then be estimated as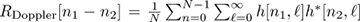 
. The Doppler spectrum could also be measured through estimating the power spectrum.
5.7.4 Signal Models for Channel Selectivity
The selectivity of a channel determines which signal processing channel model is appropriate. As a result of the decomposition of time and frequency selectivity, there are four regions of selectivity. In this section, we present typical models for each region and comment on the signal processing required at the receiver in each case.
Time Invariant/Frequency Flat
In this case, the equivalent system, including the channel, carrier frequency offset, and frame delay (supposing symbol synchronization has been performed), can be written as
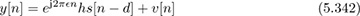
for n = 0, 1, . . . , Ntot − 1. The signal processing steps required at the receiver were dealt with extensively in Section 5.1.
Time Invariant/Frequency Selective
In this case, the equivalent system, including the channel, carrier frequency offset, and delay, is
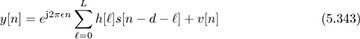
for n = 0, 1, . . . , Ntot − 1 where the impulse response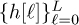 
includes the effects of multipath, the transmit pulse shape, and receive matched filter, as well as any symbol synchronization errors. The signal processing steps required at the receiver were dealt with extensively in Section 5.2 through Section 5.4.
Time Variant/Frequency Flat
Assuming that the channel changes slowly with respect to the symbol period but changes faster than TNtot,
for n = 0, 1, . . . , Ntot − 1. If the channel changes too fast relative to T, then the transmit pulse shape will be significantly distorted and a more complex linear time-varying system model will be required. We have incorporated the presence of a small carrier frequency offset into the time-varying channel; the presence of larger offsets would require a different model.
One way to change the channel estimation and equalization algorithms in Section 5.1 is to include a tracking loop. The idea is to use periodically inserted pilots (at less than the coherence time) to exploit the correlation between the samples of h[n]. In this way, an estimate of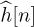 
can be generated by using concepts of prediction and estimation, for example, a Wiener or Kalman filter [172, 143]. Another approach is to avoid channel estimation altogether and resort to differential modulation techniques like DQPSK. Generally, these methods have an SNR penalty over coherent modulations but have relaxed or no channel estimation requirements [156, 287].
Time Variant/Frequency Selective
Assuming that the channel changes slowly with respect to the symbol period but changes faster than TNtot,
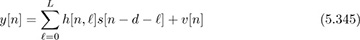
for n = 0, 1, . . . , Ntot − 1. The channel is described by a two-dimensional linear time-varying system with impulse response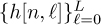 
, which is often called a doubly selective channel. We have again incorporated the presence of carrier frequency offset into the time-varying channel. If the channel changes a lot, then some additional Nyquist assumptions may need to be made and the discrete-time model would become much more complex (typically this is required only for extremely high Dopplers).
The time- and frequency-selective channel is the most challenging from a signal processing perspective because the channel taps change over time. Operating under this kind of channel is challenging for two reasons. First, estimating the channel coefficients is difficult. Second, even with the estimated coefficients, the equalizer design is also challenging. One way to approach this problem is to use basis expansion methods [213] to represent the doubly selective channel as a function of a smaller number of more slowly varying coefficients. This parametric approach can help with channel estimation. Then modifications of OFDM modulations can be used that are more suitable for time-varying channels [320, 359]. Operating in the time- and frequency-selective region is common for underwater communication [92]. It is not yet common for terrestrial systems, though there is now growing interest by companies like Cohere Technologies [230].