Dealing with Impairments in Wireless Communication

This chapter is from the book

Introduction to Wireless Digital Communication: A Signal Processing Perspective

Learn More Buy

This chapter is from the book

This chapter is from the book 

Introduction to Wireless Digital Communication: A Signal Processing Perspective

Learn More Buy

5.3 Estimating Frequency-Selective Channels

When developing algorithms for equalization, we assumed that the channel state information 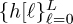was known perfectly at the receiver. This is commonly known as genie-aided channel state information and is useful for developing analysis of systems. In practice, the receiver needs to estimate the channel coefficients as engineering an all-knowing genie has proved impossible. In this section, we describe one method for estimating the channel in the time domain, and another for estimating the channel in the frequency domain. We also describe an approach for direct channel equalization in the time domain, where the coefficients of the equalizer are estimated from the training data instead of first estimating the channel and then computing the inverse. All the proposed methods make use of least squares.

5.3.1 Least Squares Channel Estimation in the Time Domain

In this section, we formulate the channel estimation problem in the time domain, making use of a known training sequence. The idea is to write a linear system of equations where the channel convolves only the known training data. From this set of equations, the least squares solution follows directly.

Suppose as in the frame synchronization case that 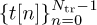is a known training sequence and that s[n] = t[n] for n = 0, 1, . . . , N_tr − 1. Consider the received signal in (5.87). We have to write y[n] only in terms of t[n]. The first few samples depend on symbols sent prior to the training data. For example,

Since prior symbols are unknown (they could belong to a previous packet or a message sent to another user, or they could even be zero, for example), they should not be included in the formulation. Taking n ∈ [L, N_tr − 1], though, gives

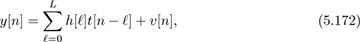
which is only a function of the unknown training data. We use these samples to form our channel estimator.

Collecting all the known samples together,

which is simply written in matrix form as

As a result, this problem takes the form of a linear parameter estimation problem, as reviewed in Section 3.5.

The least squares channel estimate, which is also the maximum likelihood estimate since the noise is AWGN, is given by

assuming that the Toeplitz training matrix T is invertible. Notice that the product (T*T)⁻¹T can be computed offline ahead of time, so the actual complexity is simply a matrix multiplication.

To be invertible, the training matrix must be square or tall, which requires that

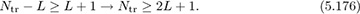
Generally, choosing N_tr much larger than L + 1 (the length of the channel) gives better performance. The full-rank condition can be guaranteed by ensuring that the training sequence is persistently exciting. Basically this means that it looks random enough. A typical design objective is to find a sequence such that T*T is (nearly) a scaled identity matrix I. This ensures that the noise remains nearly IID among other properties. Random training sequences with sufficient length usually perform well whereas t[n] = 1 will fail. Training sequences with good correlation properties generally satisfy this requirement, because the entries of T*T are different (partial) correlations of t[n].

Special training sequences can be selected from those known to have good correlation properties. One such design uses a cyclically prefixed training sequence. Let 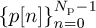be a sequence with good periodic correlation properties. This means that the periodic correlation 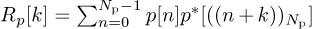satisfies the property that |R_p[k]| is small or zero for k > 0. Construct the training sequence 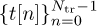by prefixing 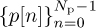with 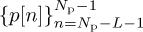, which gives an N_tr = N_p + L training sequence. With this construction

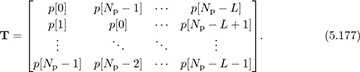
Then [T*T]_k,ℓ = R_p[k − ℓ] contains lags of the periodic correlation function. Therefore, sequences with good periodic autocorrelation properties should work well when cyclically prefixed.

In the following examples, we present designs of T based on sequences with perfect periodic autocorrelation. This results in T*T = N_pI and a simplified least squares estimate of . We consider the Zadoff-Chu sequences [70, 117] in Example 5.14 and Frank sequences [118] in Example 5.15. These designs can be further generalized to families of sequences with good cross-correlations as well; see, for example, the Popovic sequences in [267].

Example 5.14 Zadoff-Chu sequences are length N_p sequences with perfect periodic autocorrelation [70, 117], which means that R_p[k] = 0 for k ≠ 0. They have the form

where M is an integer that is relatively coprime with N_p, which could be as small as 1. Chu sequences are drawn from the N_p-PSK constellation and have length N_p.

Find a Chu sequence of length N_p = 16.

Answer: We need to find an M that is coprime with N_p. Since 16 has divisors of 2, 4, and 8, we can select any other number. For example, choosing M = 3 gives

which gives the sequence

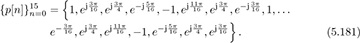
With this choice of training, it follows that T*T = N_pI.

Example 5.15 The Frank sequence [118] gives another construction of sequences with perfect periodic correlation, which uses a smaller alphabet compared to the Zadoff-Chu sequences. For n = mq + k,

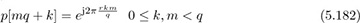
where r must be coprime with q, q is any positive integer, and n ∈ [0, q² − 1]. The length of the Frank sequence is then N_p = q² and comes from a q-PSK alphabet.

Find a length 16 Frank sequence.

Answer: Since the length of the Frank sequence is N_p = q², we must take q = 4. The only viable choice of r is 3. With this choice

for m ∈ [0, 3] and k ∈ [0, 3]. This gives the sequence

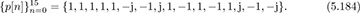
The Frank sequence also satisfies T but does so with a smaller constellation size, in this case 4-PSK. Note that a 4-QAM signal can be obtained by rotating each entry by exp(jπ/4).

A variation of the cyclic prefixed training sequence design uses both a prefix and a postfix. This approach was adopted in the GSM cellular standard. In this case, a sequence with good periodic correlation properties 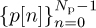is prefixed by L samples 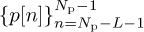and postfixed by the samples 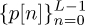. This results in a sequence with length N_tr + 2L. The motivation for this design is that

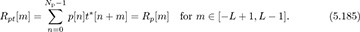
With perfect periodic correlation, the cross-correlation between p[n] and t[n] then has the form of

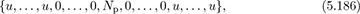
which looks like a discrete-time delta function plus some additional cross-correlation terms (represented by u; these are the values of R_pt[k] for k ≥ L). As a result, correlation with p[n], equivalently convolving with p*[(N_p − n + 1)], directly produces an estimate of the channel for certain correlation lags. For example, assuming that s[n] = t[n] for n = 0, 1, . . . , N_tr − 1,

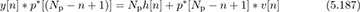
for n = N_p, N_p + 1, . . . , N_p + L. In this way, it is possible to produce an estimate of the channel just by correlating with the sequence {p[n]} that is used to compose the training sequence {t[n]}. This has the additional advantage of also helping with frame synchronization, especially when the prefix size is chosen to be larger than L, and there are some extra zero values output from the correlation.

Another training design is based on Golay complementary sequences [129]. This approach is used in IEEE 802.ad [162]. Let 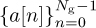and 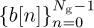be length N_g Golay complementary sequences. Such sequences satisfy a special periodic correlation property

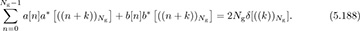
Furthermore, they also satisfy the aperiodic correlation property

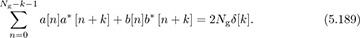
It turns out that the family of Golay complementary sequences is much more flexible than sequences with perfect periodic correlation like the Frank and Zadoff-Chu sequences. In particular, it is possible to construct such pairs of sequences from BPSK constellations without going to higher-order constellations. Furthermore, such sequence pairs exist for many choices of lengths, including for any N_g as a power of 2. There are generalizations to higher-order constellations. Overall, the Golay complementary approach allows a flexible sequence design with some additional complexity advantages.

Now construct a training sequence by taking 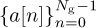, with a cyclic prefix and postfix each of length L, and naturally N_g > L. Then append another sequence constructed from 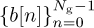with a cyclic prefix and postfix as well. This gives a length N_tr = 2N_g + 4L training sequence. Assuming that s[n] = t[n] for n = 0, 1, . . . , N_tr − 1,

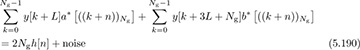
for n = 0, 1, . . . , N_g − 1. As a result, channel estimation can be performed directly by correlating the received data with the complementary Golay pair and adding the results. In IEEE 802.11ad, the Golay complementary sequences are repeated several times, to allow averaging over multiple periods, while also facilitating frame synchronization. They can also be used for rapid packet identification; for example, SC-FDE and OFDM packets use different sign patterns on the complementary Golay sequences, as discussed in [268].

An example construction of binary Golay complementary sequences is provided in Example 5.16. We provide an algorithm for constructing sequences and then use it to construct an example pair of sequences and a corresponding training sequence.

Example 5.16 There are several constructions of Golay complementary sequences [129]. Let a_m[n] and b_m[n] denote a Golay complementary pair of length 2^m. Then binary Golay sequences can be constructed recursively using the following algorithm:

Find a length N_g = 8 Golay complementary sequence, and use it to construct a training sequence assuming L = 2.

Answer: Applying the recursive algorithm gives

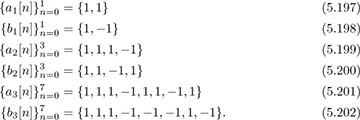
The resulting training sequence, composed of Golay complementary sequences with length L = 2 cyclic prefix and postfix, is

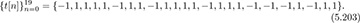
Example 5.17 IEEE 802.15.3c 60GHz is a standard for high-data-rate WPAN. In this example, we review the preamble for what is called the high-rate mode of the SC-PHY. Each preamble has a slightly different structure to make them easy to distinguish. The frame structure including the preamble is shown in Figure 5.24. Let a₁₂₈ and b₁₂₈ denote vectors that contain length 128 complementary Golay sequences (in terms of BPSK symbols), and a₂₅₆ and b₂₅₆ vectors that contain length 256 complementary Golay sequences. From the construction in Example 5.16, a₂₅₆ = [a₁₂₈; b₁₂₈] and b₂₅₆ = [a₁₂₈; −b₁₂₈] where we use ; to denote vertical stacking as in MATLAB. The specific Golay sequences used in IEEE 802.15.3c are found in [159]. The preamble consists of three components:

1. The frame detection (SYNC) field, which contains 14 repetitions of a₁₂₈ and is used for frame detection

2. The start frame delimiter (SFD), which contains [a₁₂₈; a₁₂₈; −a₁₂₈; a₁₂₈] and is used for frame and symbol synchronization

3. The channel estimation sequence (CES), which contains [b₁₂₈; b₂₅₆; a₂₅₆; b₂₅₆; a₂₅₆] and is used for channel estimation

• Why does the CES start with b₁₂₈?

  Answer: Since a₂₅₆ = [a₁₂₈; b₁₂₈], b₁₂₈ acts as a cyclic prefix.

• What is the maximum channel order supported?

  Answer: Given that b₁₂₈ is a cyclic prefix, then L_c = 128 is the maximum channel order.

• Give a simple channel estimator based on the CES (assuming that frame synchronization and frequency offset correction have already been performed).

  Answer: Based on (5.190),

  

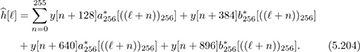
  for ℓ = 0, 1, . . . , L_c.

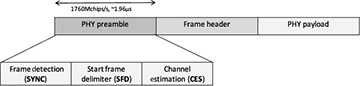
Figure 5.24 Frame structure defined in the IEEE 802.15.3c standard

In this section, we presented least squares channel estimation based on a training sequence. We also presented several training sequence designs and showed how they can be used to simplify the estimation. This estimator was constructed assuming that the training data contains symbols. This approach is valid for standard pulse-amplitude modulated systems and SC-FDE systems. Next, we present several approaches for channel estimation that are specifically designed for OFDM modulation.

5.3.2 Least Squares Channel Estimation in the Frequency Domain

Channel estimation is required for frequency-domain equalization in OFDM systems. In this section, we describe several approaches for channel estimation in OFDM, based on either the time-domain samples or the frequency-domain symbols.

First, we describe the time-domain approach. We suppose that N_tr = N, so the training occupies exactly one complete OFDM symbol. It is straightforward to generalize to multiple OFDM symbols. Suppose that the training 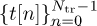is input to the IDFT, and a length L_c cyclic prefix is appended, to create 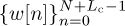. In the time-domain approach, the IDFT output samples 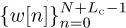are used to estimate the time-domain channel coefficients, by building T in (5.173) from w[n] and then estimating the channel from (5.175). The frequency-domain channel coefficients are then obtained from 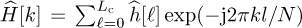. The main disadvantage of this approach is that the nice properties of the training sequence are typically lost in the IDFT transformation.

Now we describe an approach where training is interleaved with unknown data in what are called pilots. Essentially the presence of pilots means that a subset of the symbols on a given OFDM symbol are known. With enough pilots, we show that it is possible to solve a least squares channel estimation problem using only the data that appears after the IDFT operation [338].

Suppose that training data is sent on a subset of all the carriers in an OFDM symbol; using all the symbols is a special case. Let P = {p₁, p₂, . . . , p_P } denote the indices of the subcarriers that contain known training data. The approach we take is to write the observations as a function of the unknown channel coefficients. First observe that by writing the frequency-domain channel in terms of the time-domain coefficients,

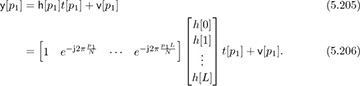
Collecting the data from the different pilots together:

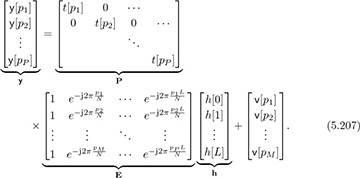
This can now be written compactly as

The matrix P has the training pilots on its diagonal. It is invertible for any choice of nonzero pilot symbols. The matrix E is constructed from samples of DFT vectors. It is tall and full rank as long as the number of pilots P ≥ L + 1. Therefore, with enough pilots, we can compute the least squares solution as

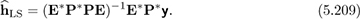
This approach allows least squares channel estimation to be applied based only on training at known pilot locations. The choice of pilot sequences with pilot estimation is not as important as in the time-domain approach; the selection of pilot locations is more important as this influences the rank properties of E. The approach can be extended to multiple OFDM symbols, possibly at different locations for improved performance.

An alternative approach for channel estimation in the frequency domain is to interpolate the frequency-domain channel estimates instead of solving a least squares problem [154]. This approach makes sense when training is sent on the same subcarrier across OFDM symbols, to allow some additional averaging over time.

Consider a comb-type pilot arrangement where P pilots are evenly spaced and N_c = N/P. This uniform spacing is optimum under certain assumptions for LMMSE channel estimation in OFDM systems [240] and for least squares estimators if P*P is a scaled identity matrix. Let 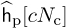be the channel estimated at the pilot locations for c = 0, 1, . . . , P −1 with 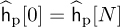and 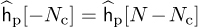to account for wrapping effects. This estimate is obtained by averaging over multiple observations of y[p_k] in multiple OFDM symbols. Using second-order interpolation, the missing channel coefficients are estimated as [77]

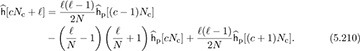
In this way, the frequency-domain channel coefficients may be estimated directly from the pilots without solving a higher-dimensional least squares problem. With a similar total number of pilots, the performance of the time-domain and interpolation algorithms can be similar [154].

There are other approaches for channel estimation that may further improve performance. For example, if some assumptions are made about the second-order statistics of the channel, and these statistics are known at the receiver, then LMMSE methods may be used. Several decibels of performance improvement, in terms of uncoded symbol error rate, may be obtained through MMSE [338]. Pilots may also be distributed over multiple OFDM symbols, on different subcarriers in different OFDM symbols. This allows two-dimensional interpolation, which is valuable in channels that change over time [196]. The 3GPP LTE cellular standard includes pilots distributed across subcarriers and across time.

Example 5.18 In this example, we explore the preamble structure used in IEEE 802.11a, shown in Figure 5.25, and explain how it is used for channel estimation [160, Chapter 17]. A similar structure is used in IEEE 802.11g, with some backward compatibility support for 802.11b, and in IEEE 802.11n, with some additions to facilitate multiple-antenna transmission. The preamble in IEEE 802.11a consists of a short training field (STF) and a channel estimation field (CEF). Each field has the duration of two OFDM symbols (8µs) but is specially constructed. In this problem, we focus on channel estimation based on the CEF, assuming that frame synchronization and carrier frequency offset correction have been performed.

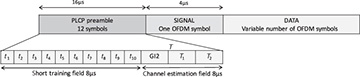
Figure 5.25 Frame structure defined in the IEEE 802.11a standard. In the time domain, the waveforms t₁ through t₁₀ are identical (ten repetitions of short training) and T₁ and T₂ are the same (two repetitions of long training). The Physical Layer Convergence Procedure (PLCP) is used to denote the extra training symbols inserted to aid synchronization and training.

The CEF of IEEE 802.11a consists of two repeated OFDM symbols, each containing training data, preceded by an extra-long cyclic prefix. Consider a training sequence of length N = 64 with values

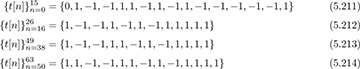
where all other subcarriers are zero. IEEE 802.11a uses zero subcarriers to help with spectral shaping; a maximum of only 52 subcarriers is used. The n = 0 subcarrier corresponds to DC and is also zero. The CEF is constructed as

for n = 0, 1, . . . , 159. Essentially the CEF has one extended cyclic prefix of length L_c = 32 (extended because it is longer than the normal L_c = 16 prefix used in IEEE 802.11a) followed by the repetition of two IDFTs of the training data. The repetition is also useful for frequency offset estimation and frame synchronization described in Section 5.4.4. Time-domain channel estimation can proceed directly using (5.215). For estimation from the frequency domain, we define two slightly different truncated received signals 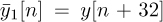and 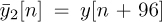for n = 0, 1, . . . , 63. Taking the DFT gives 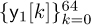and 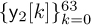. The parts of the received signal corresponding to the nonzero training 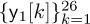, , 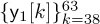, 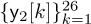and 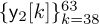can then be used for channel estimation by using a linear equation of the form

and finding the least squares solution.

5.3.3 Direct Least Squares Equalizer

In the previous sections, we developed channel estimators based on training data. These channel estimates can be used to devise equalizer coefficients. At each step in the process, both channel estimation and equalizer computation create a source of error since they involve solving least squares problems. As an alternative, we briefly review an approach where the equalizer coefficients are estimated directly from the training data. This approach avoids the errors that occur in two steps, giving somewhat more noise robustness, and does not require explicit channel estimation.

To formulate this problem, again consider the received signal in (5.87), and the signal after equalization in (5.96), which gives an expression for 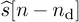. We now formulate a least squares problem based on the presence of the known training data s[n] = t[n] for n = 0, 1, . . . , N_tr. Given the location of this data, and suitably time shifting the observed sequence, gives

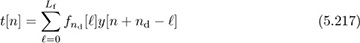
for n = 0, 1, . . . , N_tr. Building a linear equation:

In matrix form, the objective is to solve the following linear system for the unknown equalizer coefficients:

If L_f + 1 > N_tr, then Y_nd is a fat matrix, and the system of equations is undetermined. This means that there is an infinite number of exact solutions. This, however, tends to lead to overfitting, where the equalizer is perfectly matched to the observations in Y_nd. A more robust approach is to take L_f ≤ N_tr − 1, turning Y_nd into a tall matrix. It is reasonable to assume that Y_ndx is full rank because of the presence of additive noise in y[n]. Under this assumption, the least squares solution is

The squared error is measured as 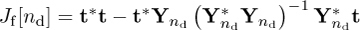. The squared error can be minimized further by choosing n_d such that J_f[n_d] is minimized.

A block diagram including direct equalization is illustrated in Figure 5.26. The block diagram assumes that the equalization computation block optimizes over the delay and outputs the corresponding filter and required delay. Direct equalization avoids the separate channel estimation and equalizer computation blocks.

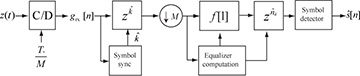
Figure 5.26 A complex pulse-amplitude modulation receiver with direct equalizer estimation and linear equalization

The direct and indirect equalization techniques have different design trade-offs. With the direct approach, the length of the training determines the maximum length of the equalizer. This is a major difference between the direct and indirect methods. With the indirect method, an equalizer of any order L_f can be designed. The direct method, however, avoids the error propagation where the estimated channel is used to compute the estimated equalizer. Note that with a small amount of training the indirect method may perform better since a larger L_f can be chosen, whereas a direct method may be more efficient when N_tr is larger. The direct method also has some robustness as it will work even when there is model mismatch, that is, when the LTI model is not quite valid or there is interference. Direct equalization can be done perfectly in multichannel systems as discussed further in Chapter 6.