Using OpenACC to Parallelize Real Code
Walk through building a real-world OpenACC, a high-level, directive-based programming model for C/C++ and Fortran, program.
In this chapter, you’ll parallelize real code. You will start with code that does something useful. Then you’ll consider how you might use OpenACC to speed it up. You will see that reducing data movement is key to achieving significant speedup, and that OpenACC gives you the tools to do so. By the end of the chapter you will be able to call yourself an OpenACC programmer—a fledgling one, perhaps, but on your way. Let’s jump right into it.
4.1 Case Study
You are reading a book about OpenACC programming, so it’s a safe bet the authors are fans of this approach to parallel programming. Although that’s a perfectly sensible thing, it has its dangers. It is tempting for enthusiasts to cherry-pick examples that make it seem as if their favored technology is perfect for everything. Anyone with experience in parallel programming has seen this before. We are determined not to do that here.
Our example is so generically useful that it has many applications, and it is often used to demonstrate programming with other parallel techniques as well, such as the somewhat related OpenMP and the very different MPI. So, rest assured, we haven’t rigged the game.
Another reason we prefer this example is that both the “science” and the numerical method are intuitive. Although we will solve the Laplace equation for steady-state temperature distribution using Jacobi iteration, we don’t expect that you immediately know what that means.
Let’s look at the physical problem. You have a square metal plate. It is initially at zero degrees. This is termed, unsurprisingly, the initial conditions. You will heat two of the edges in an interesting pattern where you heat the lower-right corner (as pictured in Figure 4.1A) to 100 degrees. You control the two heating elements that lead from this corner such that they go steadily to zero degrees at their farthest edge. The other two edges you will hold at zero degrees. These four edges constitute the boundary conditions.
For the metal plate, you would probably guess the ultimate solution should look something like Figure 4.1B.
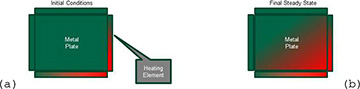
Figure 4.1. A heated metal plate
You have a very hot corner, a very cold corner, and some kind of gradient in between. This is what the ultimate, numerically solved solution should look like.
If you are wondering whether this is degrees centigrade or Fahrenheit, or maybe Kelvin, you are overthinking the problem. If you have a mathematical method or numerical background, you should be interested to know that the equation that governs heat distribution is the Laplace equation:
∇2T = 0
Although this equation has many interesting applications, including electrostatics and fluid flow, and many fascinating mathematical properties, it also has a straightforward and intuitive meaning in this context. It simply means that the value of interest (in our case, temperature) at any point is the average of the neighbor’s values. This makes sense for temperature; if you have a pebble and you put a cold stone on one side and a hot stone on the other, you’d probably guess that the pebble would come to the average of the two. And in general, you would be right.
4.1.1 Serial Code
Let’s represent the metal plate using a grid, which becomes a typical two-dimensional array in code. The Laplace equation says that every point in the grid should be the average of the neighbors. This is the state you will solve for.
The simulation starting point—the set of initial conditions—is far from this. You have zero everywhere except some big jumps along the edges where the heating elements are. You want to end up with something that resembles the desired solution.
There are many ways you can find this solution, but let’s pick a particularly straightforward one: Jacobi iteration. This method simply says that if you go over your grid and set each element equal to the average of the neighbors, and keep doing this, you will eventually converge on the correct answer. You will know when you have reached the right answer because when you make your averaging pass, the values will already be averaged (the Laplace condition) and so nothing will happen. Of course, these are floating-point numbers, so you will pick some small error, which defines “nothing happening.” In this case, we will say that when no element changes more than one-hundredth of a degree, we are done. If that isn’t good enough for you, you can easily change it and continue to a smaller error.
Your serial algorithm looks like this at the core.
for(i = 1; i <= HEIGHT; i++) {
for(j = 1; j <= WIDTH; j++) {
Temperature[i][j] = 0.25 * (Temperature_previous[i+1][j]
+ Temperature_previous[i-1][j]
+ Temperature_previous[i][j+1]
+ Temperature_previous[i][j-1]);
}
}
Here it is in Fortran:
do j=1,width
do i=1,height
temperature(i,j) =0.25*(temperature_previous(i+1,j)&
+ temperature_previous(i-1,j)&
+ temperature_previous(i,j+1)&
+ temperature_previous(i,j-1))
enddo
enddo
Note that the C and Fortran code snippets are virtually identical in construction. This will remain true for the entire program.
This nested loop is the guts of the method and in some sense contains all the science of the simulation. You are iterating over your metal plate in both dimensions and setting every interior point equal to the average of the neighbors (i.e., adding together and dividing by 4). You don’t change the very outside elements; those are the heating elements (or boundary conditions). There are a few other items in the main iteration loop as it repeats until convergence. Listing 4.1 shows the C code, and Listing 4.2 shows the Fortran code.
Listing 4.1. C Laplace code main loop
while ( worst_dt > TEMP_TOLERANCE ) {
for(i = 1; i <= HEIGHT; i++) {
for(j = 1; j <= WIDTH; j++) {
Temperature[i][j] = 0.25 * (Temperature_previous[i+1][j]
+ Temperature_previous[i-1][j]
+ Temperature_previous[i][j+1]
+ Temperature_previous[i][j-1]);
}
}
worst_dt = 0.0;
for(i = 1; i <= HEIGHT; i++){
for(j = 1; j <= WIDTH; j++){
worst_dt = fmax( fabs(Temperature[i][j]-
Temperature_previous[i][j]),
worst_dt);
Temperature_previous[i][j] = Temperature[i][j];
}
}
if((iteration % 100) == 0) {
track_progress(iteration);
}
iteration++;
}
Listing 4.2. Fortran Laplace code main loop
do while ( worst_dt > temp_tolerance )
do j=1,width
do i=1,height
temperature(i,j) =0.25*(temperature_previous(i+1,j)&
+ temperature_previous(i-1,j)&
+ temperature_previous(i,j+1)&
+ temperature_previous(i,j-1))
enddo
enddo
worst_dt=0.0
do j=1,width
do i=1,height
worst_dt = max( abs(temperature(i,j) – &
temperature_previous(i,j)),&
worst_dt )
temperature_previous(i,j) = temperature(i,j)
enddo
enddo
if( mod(iteration,100).eq.0 ) then
call track_progress(temperature, iteration)
endif
iteration = iteration+1
enddo
The important addition is that you have a second array that keeps the temperature data from the last iteration. If you tried to use one array, you would find yourself using some updated neighboring elements and some old neighboring elements from the previous iteration as you were updating points in the grid. You need to make sure you use only elements from the last iteration.
While you are doing this nested loop copy to your backup array (and moving all this data around in memory), it’s a good time to look for the worst (most changing) element in the simulation. When the worst element changes only by 0.01 degree, you know you are finished.
It might also be nice to track your progress as you go; it’s much better than staring at a blank screen for the duration. So, every 100 iterations, let’s call a modest output routine.
That is all there is to it for your serial Laplace Solver. Even with the initialization and output code, the full program clocks in at fewer than 100 lines. (See Listing 4.3 for the C code, and Listing 4.4 for Fortran.)
Listing 4.3. Serial Laplace Solver in C
#include <stdlib.h>
#include <stdio.h>
#include <math.h>
#include <sys/time.h>
#define WIDTH 1000
#define HEIGHT 1000
#define TEMP_TOLERANCE 0.01
double Temperature[HEIGHT+2][WIDTH+2];
double Temperature_previous[HEIGHT+2][WIDTH+2];
void initialize();
void track_progress(int iter);
int main(int argc, char *argv[]) {
int i, j;
int iteration=1;
double worst_dt=100;
struct timeval start_time, stop_time, elapsed_time;
gettimeofday(&start_time,NULL);
initialize();
while ( worst_dt > TEMP_TOLERANCE ) {
for(i = 1; i <= HEIGHT; i++) {
for(j = 1; j <= WIDTH; j++) {
Temperature[i][j] = 0.25 * (Temperature_previous[i+1][j]
+ Temperature_previous[i-1][j]
+ Temperature_previous[i][j+1]
+ Temperature_previous[i][j-1]);
}
}
worst_dt = 0.0;
for(i = 1; i <= HEIGHT; i++){
for(j = 1; j <= WIDTH; j++){
worst_dt = fmax( fabs(Temperature[i][j]-
Temperature_previous[i][j]),
worst_dt);
Temperature_previous[i][j] = Temperature[i][j];
}
}
if((iteration % 100) == 0) {
track_progress(iteration);
}
iteration++;
}
gettimeofday(&stop_time,NULL);
timersub(&stop_time, &start_time, &elapsed_time);
printf("\nMax error at iteration %d was %f\n",
iteration-1, worst_dt);
printf("Total time was %f seconds.\n",
elapsed_time.tv_sec+elapsed_time.tv_usec/1000000.0);
}
void initialize(){
int i,j;
for(i = 0; i <= HEIGHT+1; i++){
for (j = 0; j <= WIDTH+1; j++){
Temperature_previous[i][j] = 0.0;
}
}
for(i = 0; i <= HEIGHT+1; i++) {
Temperature_previous[i][0] = 0.0;
Temperature_previous[i][WIDTH+1] = (100.0/HEIGHT)*i;
}
for(j = 0; j <= WIDTH+1; j++) {
Temperature_previous[0][j] = 0.0;
Temperature_previous[HEIGHT+1][j] = (100.0/WIDTH)*j;
}
}
void track_progress(int iteration) {
int i;
printf("---------- Iteration number: %d ------------\n",
iteration);
for(i = HEIGHT-5; i <= HEIGHT; i++) {
printf("[%d,%d]: %5.2f ", i, i, Temperature[i][i]);
}
printf("\n");
}
Listing 4.4. Fortran version of serial Laplace Solver
program serial
implicit none
integer, parameter :: width=1000
integer, parameter :: height=1000
double precision, parameter :: temp_tolerance=0.01
integer :: i, j, iteration=1
double precision :: worst_dt=100.0
real :: start_time, stop_time
double precision, dimension(0:height+1,0:width+1) :: &
temperature, temperature_previous
call cpu_time(start_time)
call initialize(temperature_previous)
do while ( worst_dt > temp_tolerance )
do j=1,width
do i=1,height
temperature(i,j) = 0.25* (temperature_previous(i+1,j)&
+ temperature_previous(i-1,j)&
+ temperature_previous(i,j+1)&
+ temperature_previous(i,j-1))
enddo
enddo
worst_dt=0.0
do j=1,width
do i=1,height
worst_dt = max( abs(temperature(i,j) – &
temperature_previous(i,j)),&
worst_dt )
temperature_previous(i,j) = temperature(i,j)
enddo
enddo
if( mod(iteration,100).eq.0 ) then
call track_progress(temperature, iteration)
endif
iteration = iteration+1
enddo
call cpu_time(stop_time)
print*, 'Max error at iteration ', iteration-1, ' was ', &
worst_dt
print*, 'Total time was ',stop_time-start_time, ' seconds.'
end program serial
subroutine initialize( temperature_previous )
implicit none
integer, parameter :: width=1000
integer, parameter :: height=1000
integer :: i,j
double precision, dimension(0:height+1,0:width+1) :: &
temperature_previous
temperature_previous = 0.0
do i=0,height+1
temperature_previous(i,0) = 0.0
temperature_previous(i,width+1) = (100.0/height) * i
enddo
do j=0,width+1
temperature_previous(0,j) = 0.0
temperature_previous(height+1,j) = ((100.0)/width) * j
enddo
end subroutine initialize
subroutine track_progress(temperature, iteration)
implicit none
integer, parameter :: width=1000
integer, parameter :: height=1000
integer :: i,iteration
double precision, dimension(0:height+1,0:width+1) :: &
temperature
print *, '------- Iteration number: ', iteration, ' ------'
do i=5,0,-1
write (*,'("("i4,",",i4,"):",f6.2," ")',advance='no') &
height-i,width-i,temperature(height-i,width-i)
enddo
print *
end subroutine track_progress
4.1.2 Compiling the Code
Take a few minutes to make sure you understand the code fully. In addition to the main loop, you have a small bit of initialization, a timer to aid in optimizing, and a basic output routine. This code compiles as simply as
pgcc laplace.c
Here it is for the PGI compiler:
pgcc laplace.f90
We use PGI for performance consistency in this chapter. Any other standard compiler would work the same. If you run the resulting executable, you will see something like this:
. . . . . . ---------- Iteration number: 3200 ------------ . . . [998,998]: 99.18 [999,999]: 99.56 [1000,1000]: 99.86 ---------- Iteration number: 3300 ------------ . . . [998,998]: 99.19 [999,999]: 99.56 [1000,1000]: 99.87 Max error at iteration 3372 was 0.009995 Total time was 21.344162 seconds.
The output shows that the simulation looped 3,372 times before all the elements stabilized (to within our 0.01 degree tolerance). If you examine the full output, you can see the elements converge from their zero-degree starting point.
The times for both the C and the Fortran version will be very close here and as you progress throughout optimization. Of course, the time will vary depending on the CPU you are using. In this case, we are using an Intel Broadwell running at 3.0 GHz. At the time of this writing, it is a very good processor, so our eventual speedups won’t be compared against a poor serial baseline.
This is the last time you will look at any code outside the main loop. You will henceforth exploit the wonderful ability of OpenACC to allow you to focus on a small portion of your code—be it a single routine, or even a single loop—and ignore the rest. You will return to this point when you are finished.