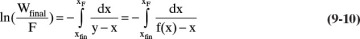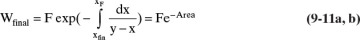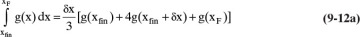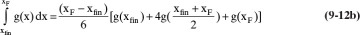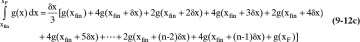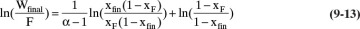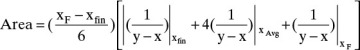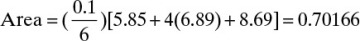- 9.0 Summary-Objectives
- 9.1 Introduction to Batch Distillation
- 9.2 Batch Distillation: Rayleigh Equation
- 9.3 Simple Binary Batch Distillation
- 9.4 Constant-Mole Batch Distillation
- 9.5 Batch Steam Distillation
- 9.6 Multistage Binary Batch Distillation
- 9.7 Multicomponent Simple Batch Distillation
- 9.8 Operating Time
- References
- Homework
- Chapter 9 Appendix A. Spreadsheet for Simple Multicomponent Batch Distillation, Constant Relative Volatility
This chapter is from the book
This chapter is from the book
This chapter is from the book
9.3 Simple Binary Batch Distillation
In the simple binary batch distillation system shown in Figure 9-1 the vapor product is in equilibrium with liquid in the still pot at any given time. Since we use a total condenser, y = xD. Substituting equilibrium into Eq. (9-7), we have
)
where y and x are in equilibrium with equilibrium expression y = f(x,p). For any given equilibrium expression, Eq. (9-10) can be integrated analytically, graphically, or numerically.
The general graphical or numerical integration procedure for Eq. (9-10) is:
Plot or fit the y-x equilibrium curve.
At a series of x values, find y – x.
Plot 1/(y – x) vs. x or fit it to an equation.
Graphically (Figure 9-4) or numerically integrate from xF to xfin.
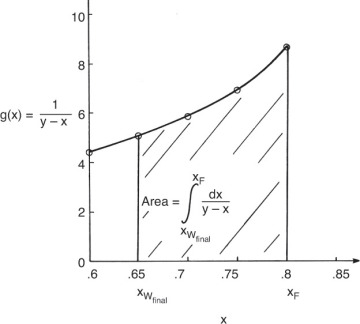
FIGURE 9-4 Graphical integration for simple batch distillation, Example 9-1
From Eq. (9-10), find the final charge of material Wfinal in the still pot:
where the area is shown in Figure 9-4.
The amount of distillate, D, and the average distillate concentration, xD,avg, can be found from the mass balances Eqs. (9-8a) and (9-8b).
)
)
The Rayleigh equation can also be integrated numerically. One convenient method for doing this is to use Simpson’s rule (e.g., see Mickley et al., 1957, pp. 35–42; or Larsson et al., 2014, pp. 42–52). If the ordinate in Figure 9-4 is called g(x), then the simplest form of Simpson’s rule divides the interval into two equal parts with δx = (xF – xfin)/2.
)
which is often written for batch distillation as
)
Terms are shown in Figure 9-4. Simpson’s rule is exact if g(x) is cubic or lower order. More accuracy can be obtained by dividing the interval into a larger, even number of parts of equal size. For example, if we use n equal subintervals, then δx = (xF – xfin)/n, and Simpson’s rule becomes
)
Note that n has to be an even integer. For smooth curves, such as in Figure 9-4, Simpson’s rule is quite accurate (see Example 9-1). For more complex shapes, Simpson’s rule may be more accurate if the integration is done in two or more separate pieces (see Example 9-2). Alternatively, half intervals can be used in regions where more accuracy is needed (Larsson et al., 2014). Simpson’s rule is also the MATLAB command quad (for quadrature) (Pratap, 2006). Other integration formulas that are more accurate can be used.
If the average distillate concentration is specified, a trial-and-error procedure is required. This involves guessing the final still pot concentration, xW,final, and calculating the area in Figure 9-4 either graphically or using Simpson’s rule. Then Eq. (9-11) gives Wfinal, and Eq. (9-8b) is used to check the value of xD,avg. For a graphical solution, the trial-and-error procedure can be conveniently carried out by starting with a guess for xfin that is too high. Then every time xfin is decreased, the additional area is added to the area already calculated.
If the relative volatility α is constant, the Rayleigh equation can be integrated analytically. In this case the equilibrium expression is Eq. (2-22b), which is repeated here:
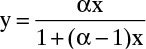
Substituting this equation into Eq. (9-10) and integrating, we obtain
)
When it is applicable, Eq. (9-13) is obviously easier to apply than graphical or numerical integration. Analytical solutions for limiting cases (constant α in this case) are also useful for checking numerical solutions.
Warning: If α is not constant, Wfinal calculated from Eq. (9-13) can be very inaccurate.
EXAMPLE 9-1. Simple binary Rayleigh distillation
A simple batch still (one equilibrium stage) is separating a 50 mole feed charge to the still pot that is 80.0 mol% methanol and 20.0 mol% water. An average distillate concentration of 89.2 mol% methanol is required. Find the amount of distillate collected, the amount of material left in the still pot, and the concentration of the material in the still pot. Pressure is 1 atm.
Solution
Define. The apparatus is shown in Figure 9-1. The conditions are: p = 1 atm, F = 50, xF = 0.80, and xD,avg = 0.892. Find xfin, Dtot, and Wfinal.
Explore. Since the still pot acts as one equilibrium contact, the Rayleigh equation takes the form of Eqs. (9-10) and (9-11). To use these equations, either a plot of 1/(y – x)equil vs. x is required for graphical integration or Simpson’s rule can be used. Both are illustrated. Since xfin is unknown, a trial-and-error procedure is required for either integration routine.
Plan. First plot 1/(y – x) vs. x from the equilibrium data. The trial-and-error procedure is as follows:
Guess xfin.
Integrate to find
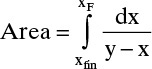
Calculate Wfinal from the Rayleigh equation and xD,avg,calc from mass balance.
Check: Is xD,avg,calc = xD,avg? If not, continue trial and error.
Do it. From the equilibrium data in Table 2-7 the following table is generated:
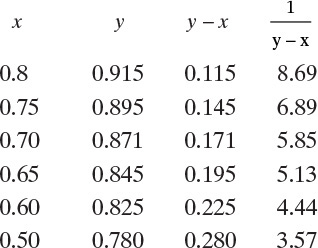
These data are plotted in Figure 9-4. For the numerical solution a large graph on millimeter graph paper was constructed.
First guess: xfin = 0.70.
From Figure 9-4,
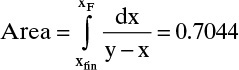
Then, Wfinal = F exp(–Area) = 50 e–0.7044 = 24.72
Dcalc = F – Wfinal = 25.28
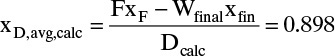
The alternative integration procedure using Simpson’s rule gives
Where
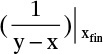is the value of 1/(y – x) calculated at xfin, and xAvg = (xF + xfin)/2.For Simpson’s rule, Wfinal = 24.79, Dcalc = 25.21, and xD,calc = 0.898. Simpson’s rule appears to be quite accurate in this case. Wfinal is off by 0.3%, and xD,calc is the same as the more exact calculation. These values appear to be close to the desired value, but we do not yet know the sensitivity of the calculation.
Second guess: xfin = 0.60. Calculations similar to the first trial give:
Area = 1.2084, Wfinal = 14.93, Dcalc = 35.07, xD,calc = 0.885 from Figure 9-4, and xD,calc = 0.884 from the Simpson’s rule calculation. These are also close, but they are low. For this problem the value of xD is insensitive to xfin.
Third guess: xfin = 0.65. Calculations give:
Area = 0.971, Wfinal = 18.94, Dcalc = 31.06, and xD,calc = 0.891 from Figure 9-4 and xD,calc = 0.890 from the Simpson’s rule calculation of the area, which are both close to the specified value of 0.892.
Thus, use xfin = 0.65 as the answer.
Check. The overall mass balance is Wfinal xfin + Dcalc xD,calc = 39.985 as compared to FxF = 40. Error is (40 – 39.985)/40 × 100, or 0.038%, which is acceptable.
Generalize. The integration can also be done numerically on a computer using Simpson’s rule or an alternative integration method. This is an advantage, since then the entire trial-and-error procedure can be programmed. Note that large differences in xW,final and hence in Wfinal cause rather small differences in xD,avg. Thus, for this problem, exact control of the batch system may not be critical. This problem illustrates a common difficulty of simple batch distillation—a pure distillate and a pure bottoms product cannot be obtained unless the relative volatility is very large. Note that although Eq. (9-13) is strictly not applicable since methanol-water equilibrium does not have a constant relative volatility, it could be used over the limited range of this batch distillation.
If xfin is very low, then
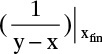becomes very large, and Simpson’s rule is not very accurate. If the area is divided into two parts from xF to x ∼ 0.05 and from this point to xfin, Simpson’s rule will be accurate for the first part. Calculate Wfin,1 from Simpson’s rule. A reasonably accurate value of relative volatility can be estimated from αAB = (yA/xA)/(yB/xB) calculated from this point. Then Eq. (9-13) will give an accurate estimate of Wfin with F = Wfin,1 and xF set equal to the point used to divide the integral.
)
)
It is interesting to compare the simple binary batch distillation result to binary flash distillation of the same feed producing y = 0.892 mole fraction methanol. This flash distillation problem was solved previously as Problem 2.D1g. The results were x = 0.756 (compare to xfin = 0.65), V = 16.18 (compare to Dtotal = 31.06), and L = 33.82 (compare to Wfinal = 18.94). The simple batch distillation gives a greater separation with more distillate product because the bottoms product is an average of liquids in equilibrium with vapor in the entire range from y = 0.915 (in equilibrium with x = z = 0.8) to y = 0.845 (in equilibrium with x = xfin = 0.65), while for the flash distillation, the liquid is always in equilibrium with the final vapor y = 0.892. In general, a simple batch distillation will give more separation than flash distillation with the same operating conditions. However, because flash distillation is continuous, it is much easier to integrate into a continuous plant.
Extension of the solution method for simple binary batch distillation to collection of fractions is straightforward if the values of xW1, xW2, ... are specified. Equations (9-9) are converted to simple batch by replacing xD with y, which is in equilibrium with xW. In essence, a number of simple batch problems are solved sequentially (see Problem 9.D23).
Extension of the simple batch equations to multicomponent systems is also straightforward, although solution of the equations is significantly more difficult than solution of the binary equations. For simple multicomponent batch distillation Eq. (9-5b) becomes
)
The Rayleigh Eq. (9-10) can be written for each component. The equilibrium expression becomes a function of all the components, which couples all of the equations. Section 9.6 explores multicomponent simple distillation in detail.
A process that is closely related to simple batch distillation is differential condensation (Treybal, 1980). In this process vapor is slowly condensed, and the condensate liquid is rapidly withdrawn. A derivation similar to the derivation of the Raleigh equation for a binary system gives
)
){kind=link}
where F is the moles of feed vapor of mole fraction yF, and Dfinal is the leftover vapor distillate of mole fraction yD,final. Differential condensation is rarely practiced.