- Random Numbers and Probability Distributions
- Casino Royale: Roll the Dice
- Normal Distribution
- The Student Who Taught Everyone Else
- Statistical Distributions in Action
- Hypothetically Yours
- The Mean and Kind Differences
- Worked-Out Examples of Hypothesis Testing
- Exercises for Comparison of Means
- Regression for Hypothesis Testing
- Analysis of Variance
- Significantly Correlated
- Summary
Worked-Out Examples of Hypothesis Testing
The best way of mastering a new concept is to practice the concept with more examples. Here I present additional worked-out examples of the t-test. I encourage you to repeat the analysis presented in these examples with a handheld calculator to get a real feel of the concepts.
Best Buy–Apple Store Comparison
Assuming unequal variances, let us see whether the average daily sales between fictional versions of a Best Buy (BB) outlet and an Apple Store (AS) are statistically different. Here are some cooked up numbers.
- BB: Average daily sales $110,000, SD $5000, sales observed for 65 days
- AS: Average sales $125,000, SD $15,000, sales observed for 45 days
Recall that we conduct a t-test to determine the significance in the difference in means for a particular characteristic of two independent groups. Equation 6.6 presents the t-test formula for unequal variances.
Subscript 1 represents statistics for Best Buy, and subscript 2 represents statistics for the Apple Store. The shape of the t-distribution depends on the degrees of freedom, which was presented earlier in Equation 6.7.
The dof are needed to determine the probability of obtaining a t-value as extreme as the one calculated here. When I plug in the numbers in the equations, I obtain the following results:
- t = –6.46
- dof = 50.82
The absolute t-stat value of –6.4 is significantly greater than the absolute value for +/–1.96, suggesting that the Best Buy outlet and the Apple Store sales are significantly different (using a two-tailed test) for large samples at the 95% confidence level. Let us obtain the critical value for the t-test that is commensurate with the appropriate sample size.
If I were to consult the t-table for dof = 50, (the closest value to 50.8) the largest t-value reported is 3.496, which is less than the one I have obtained (–6.46). Note that I refer here to the absolute value of –6.46. The corresponding probability value from the t-table for a two-tailed test for the maximum reported t-test of 3.496 is 0.001 (see the highlighted values in the image from the t-table in Figure 6.34). Thus, I can conclude that the probability of finding such an extreme t-value is less than 0.001% (two-tailed test).
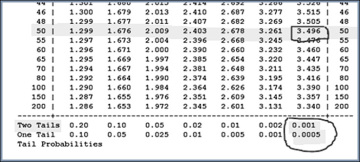
Figure 6.34 T-distribution table
I would now like to test whether Best Buy Store sales are lower than that of the Apple Stores. A one-tailed test will help us determine whether the average sales at the fictional versions of BestBuy are lower than at the Apple Store. The probability to obtain a t-value of –6.46 or higher is 0.0005% (see Figure 6.34). This suggests that the fictional BestBuy average daily sales are significantly lower than that of the Apple Store.
A p-value of less than 0.05 leads us to reject the null hypothesis that x1 > x2 and conclude that the Best Buy sales are lower than that of the Apple Store at the 95% confidence level.
Assuming Equal Variances
I repeat the preceding example now assuming equal variances. Equation 6.8 provides the standard deviation of the sampling distribution of the means. Equation 6.9 describes the pooled estimate of variance, whereas Equation 6.10 describes the test statistics.
Here is the R code:
vpool= (s1^2*(n1-1)+s2^2*(n2-1))/(n1+n2-2); sdev = sqrt(vpool*(n1+n2)/(n1*n2)) t = (x1-x2)/sdev ; dof= n1+n2-2 t = -7.495849 dof =108 vpool = 106481481 sdev = 2001.108
Notice that when I assume equal variances, I get an even stronger t-value of –7.49, which is again much larger than the absolute value for 1.96. Hence, I can conclude both for one- and two-tailed tests that Best Buy sales (assumed values) on average are lower than that of the average daily (fictional) sales for the Apple Store.
The closest value on the t-table for 108 (dof) is 100. The highest value reported along the 100 dof row is 3.390, which is lower than the absolute value of –7.49, which I estimated from the test. This suggests that the probability for a two-tailed test will be even smaller than 0.001 and for a one-tailed test will be less than 0.0005, allowing us to reject the null hypothesis.
Comparing Sales from an Urban and Suburban Retailer
A franchise operates stores in urban and suburban locations. The managers of two stores are competing for promotion. The manager at the suburban store is liked by all while the manager in the downtown location has a reputation of being a hot-head. The stores’ weekly sales data over a 50-week period are as follows:
Downtown Store |
Suburban Store |
Average weekly sales = $800,000 std dev = $100,000 n1 = 50 |
Average weekly sales = $780,000 std dev = $30,000 n2 = 50 |
Hypothesis:
- H0: x1= x2
- Ha: x1 ≠ x2
Assuming unequal variances:
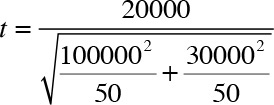
The calculations return t = 1.35 and the dof = 57.75. The p-value for the test from the t-distribution table is approximately equal to 0.15. I therefore fail to reject the null hypothesis and conclude that both stores on average generate the same revenue. Thus, the manager of the suburban store, who happens to be a nice person but appears to be selling $20,000 per week less in sales, could also be considered for promotion because the t-test revealed that the difference in sales was not statistically significant. Also remember that t = 1.35 should have made the conclusion easier because the calculated t-value is less than 1.96 for a two-tailed test.

