Getting Started with Data Science: Hypothetically Speaking

This chapter is from the book

Getting Started with Data Science: Making Sense of Data with Analytics

Learn More Buy

This chapter is from the book

This chapter is from the book 

Getting Started with Data Science: Making Sense of Data with Analytics

Learn More Buy

Hypothetically Yours

Most empirical analysis involves comparison of two or more statistics. Data scientists and analysts are often asked to compare costs, revenues, and other similar metrics related to socioeconomic outcomes. Often, this is accomplished by setting up and testing hypotheses. The purpose of the analysis is to determine whether the difference in values between two or more entities or outcomes is a result of chance or whether fundamental and statistically significant differences are at play. I explain this in the following section.

Consistently Better or Happenstance

Nate Silver, the former blogger for the New York Times and founder of fivethirtyeight.com has been at the forefront of popularizing data-driven analytics. His blogs are followed by hundreds of thousands readers. He is also credited with popularizing the use of data and analytics in sports. The same trend was highlighted in the movie Moneyball, in which a baseball coach with a data-savvy assistant puts together a team of otherwise regular players who were more likely to win as a team. The coach and his assistant, instead of relying on the traditional criterion, based their decisions on data. They were, therefore, able to put together a winning team.

Let me illustrate hypothesis testing using basketball as an example. Michael Jordan is one of the greatest basketball players. He was a consistently high scorer throughout his career. In fact, he averaged 30.12 points per game in his career, which is the highest for any basketball player in the NBA.⁴ He spent most of his professional career playing for the Chicago Bulls. Jordan was inducted into the Hall of Fame in 2009. In his first professional season in 1984–85, Jordan scored on average 28.2 points per game. He recorded his highest seasonal average of 37.1 points per game in the 1986–87 season. His lowest seasonal average of 20 points per game was observed toward the end of his career in the 2002–03 season.

Another basketball giant is Wilt Chamberlain, who is one of basketball’s first superstars and is known for his skill, conspicuous consumption, and womanizing. With 30.07 points on average per game, Chamberlain is a close second to Michael Jordan for the highest average points scored per game. Whereas Michael Jordan’s debut was in 1984, Chamberlain began his professional career with the NBA in 1959 and was inducted into the Hall of Fame in 1979.

Just like Michael Jordan, who scored the highest average points per game in his third professional season, Chamberlain also scored an average of 50.4 points per game in 1961–6, his third season. Again, just like Michael Jordan, Chamberlain’s average dropped at the tail end of his career when he scored 13.2 points per game on average in 1972–73.

Jordan’s 30.12 points per game on average and Chamberlain’s 30.06 points per game on average are very close. Notice that I am referring here to average points per game weighted by the number of games played in each season. A simple average computed from the average of points per game per season will return slightly different results.

While both Jordan and Chamberlain report very similar career averages, there are, however, significant differences in the consistency of their performance throughout their careers. Instead of the averages, if we compare standard deviations, we see that Jordan with a standard deviation of 4.76 points is much more consistent in his performance than Chamberlain was with a standard deviation of 10.59 points per game. If we were to assume that these numbers are normally distributed, I can plot the Normal curves for their performance. Note in Figure 6.15 that Michael Jordan’s performance returns a sharper curve (colored in black), whereas Chamberlain’s curve (colored in gray) is flatter and spread wide. We can see that Jordan’s score is mostly in the 20 to 40 points per game range, whereas Chamberlain’s performance is spread over a much wider interval.

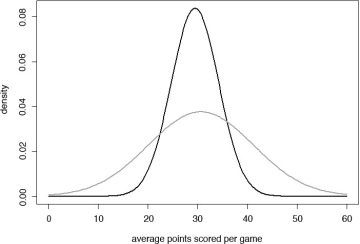
Figure 6.15 Normal distribution curves for Michael Jordan and Wilt Chamberlain

Mean and Not So Mean Differences

I use statistics to compare the consistency of scoring between two basketball giants. The comparison of means (averages) comes in three flavors. First, you can assume that the mean points per game scored by both Jordan and Chamberlain are the same. That is, the difference between the mean scores of the two basketball legends is zero. This becomes our null hypothesis. Let μ_j represent the average points per game scored by Jordan and μ_c represent the average points per game scored by Chamberlain. My null hypothesis, denoted by H₀, is expressed as follows:

• H₀:μ_j = μ_c

The alternative hypothesis, denoted as H_a, is as follows:

• H_a:μ_j ≠ μ_c; their average scores are different.

Now let us work with a different null hypothesis and assume that Michael Jordan, on average, scored higher than Wilt Chamberlain did. Mathematically:

• H₀:μ_j > μ_c

The alternative hypothesis will state that Jordan’s average is lower than that of Chamberlain’s, H_a:μ_j < μ_c. Finally, I can restate our null hypothesis to assume that Michael Jordan, on average, scored lower than Wilt Chamberlain did. Mathematically:

• H₀:μ_j < μ_c

The alternative hypothesis in the third case will be as follows:

• H_a:μ_j > μ_c; Jordan’s average is higher than that of Chamberlain’s.

I can test the hypothesis using a t-test, which I will explain later in the chapter.

Another less common test is known as the z-test, which is based on the normal distribution. Suppose a basketball team is interested in acquiring a new player who has scored on average 14 points per game. The existing team’s average score has been 12.5 points per game with a standard deviation of 2.8 points per game. The team’s manager wants to know whether the new player is indeed a better performer than the existing team. The manager can use the z-test to find the answer to this riddle. I explain the z-test in the following section.

Handling Rejections

After I state the null and alternative hypotheses, I conduct the z- or the t-test to compare the difference in means. I calculate a value for the test and compare it against the respective critical value. If the calculated value is greater than the critical value, I can reject the null hypothesis. Otherwise, I fail to reject the null hypothesis.

Another way to make the call on the hypothesis tests is to see whether the calculated value falls in the rejection region of the probability distribution function. The fundamental principal here is to determine, given the distribution, how likely it is to get a value as extreme as the one we observed. More often than not, we use the 95% threshold. We would like to determine whether the likelihood of obtaining the observed value for the test is less than 5% for a 95% confidence level. If the calculated value for the z- or the t-test falls in the region that covers the 5% of the distribution, which we know as the rejection region, we reject the null hypothesis. I illustrate the regions for normal and t-distributions in the following sections.

Normal Distribution

Recall from the last section that the alternative hypothesis comes in three flavors: The difference in means is not equal to 0, the difference is greater than 0, and the difference is less than 0. We have three rejection regions to deal with the three scenarios.

Let us begin with the scenario where the alternative hypothesis is that the mean difference is not equal to 0. We are not certain whether it is greater or less than zero. We call this the two-tailed test. We will define a rejection region in both tails (left and right) of the normal distribution. Remember, we only consider 5% of the area under the normal curve to define the rejection region. For a two-tailed test, we divide 5% into two halves and define rejection regions covering 2.5% under the curve in each tail, which together sum up to 5%. See the two-tailed test illustrated in Figure 6.16.

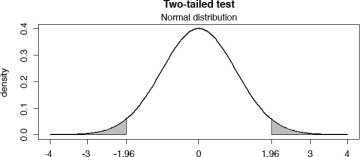
Figure 6.16 Two-tailed test using Normal distribution

Recall that the area under the normal density plot is 1. The gray-shaded area in each tail identifies the rejection region. Taken together, the gray area in the left (2.5% of the area) and in the right (2.5% of the area) constitute the 5% rejection region. If the absolute value of the z-test is greater than the absolute value of 1.96, we can safely reject the null hypothesis that the difference in means is zero and conclude that the two average values are significantly different.

Let us now consider a scenario where we believe that the difference in means is less than zero. In the Michael Jordan–Wilt Chamberlain example, we are testing the following alternative hypothesis:

• H_a:μ_j < μ_c; Jordan’s average is lower than that of Chamberlain’s.

In this particular case, I will only define the rejection region in the left tail (the gray-shaded area) of the distribution. If the calculated z-test value is less than –1.64, for example, –1.8, we will know that it falls in the rejection region (see Figure 6.17) and we will reject the null hypothesis that the difference in means is greater than zero. The test is also called one-tailed test.

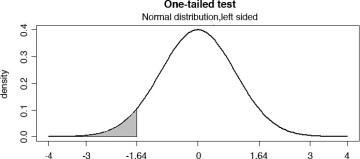
Figure 6.17 One-tailed test (left-tail)

Along the same lines, let us now consider a scenario where we believe that the difference in means is greater than zero. In the Michael Jordan–Wilt Chamberlain example, we are testing the following alternative hypothesis:

• H_a:μ_j > μ_c; Jordan’s average is higher than that of Chamberlain’s.

In this particular case, I will only define the rejection region (the gray-shaded area) in the right tail of the distribution. If the calculated z-test value is greater than 1.64, for example, 1.8, we will know that it falls in the rejection region (see Figure 6.18) and we will reject the null hypothesis that the difference in means is less than zero.

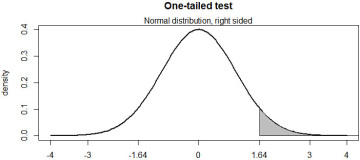
Figure 6.18 One-tailed test (right-tail)

t-distribution

Unlike the z-test, most comparison of means tests are performed using the t-distribution, which is preferred because it is more sensitive to small sample sizes. For large sample sizes, the t-distribution approximates the normal distribution. Those interested in this relationship should explore the central limit theorem. For the readers of this text, suffice it to say that for large sample sizes, the distribution looks and feels like the normal distribution, a phenomenon I have already illustrated in Figure 6.7.

I have chosen not to illustrate the rejection regions for the t-distribution, because they look the same as the ones I have illustrated for the normal distribution for sample sizes of say 200 or greater. Instead, I define the critical t-values.

As the number of observations increases, the critical t-values approach the ones we obtain from the z-test. For a left tail (mean is less than zero) test with 30 degrees of freedom, the critical value for a t-test at 5% level is –1.69. However, for a large sample with 400 degrees of freedom, the critical value is –1.648, which comes close to –1.64 for the normal distribution. Thus, one can see from Figure 6.19 that the critical values for t-distribution approaches the ones for normal distribution for larger samples. I, of course, would like to avoid the controversy for now on what constitutes as a large sample.

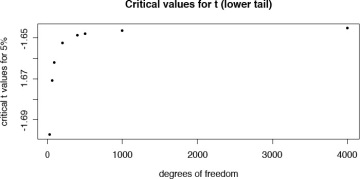
Figure 6.19 Critical t-values for left-tail test for various sample sizes

General Rules Regarding Significance

Another way of testing the hypothesis is to use the probability values associated with the z- or the t-test. Consider the general rules listed in Table 6.4 for testing statistical significance.

Table 6.4 Rules of Thumb for Hypothesis Testing

Note that for t-tests, the 1.96 threshold works with large samples. For smaller samples, the critical t-value will be larger and depend upon the degrees of freedom (the sample size).