- Random Numbers and Probability Distributions
- Casino Royale: Roll the Dice
- Normal Distribution
- The Student Who Taught Everyone Else
- Statistical Distributions in Action
- Hypothetically Yours
- The Mean and Kind Differences
- Worked-Out Examples of Hypothesis Testing
- Exercises for Comparison of Means
- Regression for Hypothesis Testing
- Analysis of Variance
- Significantly Correlated
- Summary
This chapter is from the book
This chapter is from the book
This chapter is from the book
Significantly Correlated
Often we are interested in determining the independence between two categorical variables. Let us revisit the teaching ratings data. The university administration might be interested to know whether the instructor’s gender is independent of the tenure status. This is of interest because in the presence of a gender bias, we might find that a larger proportion of women (or men) have not been granted tenure. A chi-square test of independence can help us with this challenge.
The null hypothesis (H0) states that the two categorical variables are statistically independent, whereas the alternative hypothesis (Ha) states that the two categorical variables are statistically dependent. The test statistics is expressed shown in Equation 6.11.
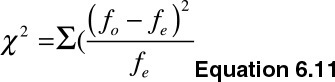
Where fo is the observed frequency, and fe is the expected frequency. We reject the null hypothesis if the p-value is less than the threshold for rejection (1-α) and the degrees of freedom.
Let us test the independence assumption between gender and tenure in the teaching ratings data set. My null hypothesis states that the two variables are statistically independent. I run the test in R and report the results in Figure 6.40. Because the p-value of 0.1098 is greater than 0.05, I fail to reject the null hypothesis that the two variables are independent and conclude that a systematic association does exist between gender and tenure.
)
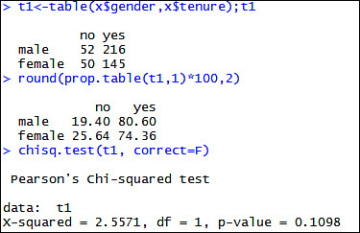
Figure 6.40 Pearson’s chi-squared test to determine association between gender and tenure status of instructors
We can easily reproduce the results in a spreadsheet or statistics software. The fe in the formula is calculated as follows:
- Determine the row and column totals for the contingency table (t1 in the last example: see the following code)
- Determine the sum of all observations in the contingency table
- Multiply the respective row and column totals and divide them by the sum of all observations to obtain fe.
The R code required to replicate the programmed output follows.
t1<-table(x$gender,x$tenure);t1 round(prop.table(t1,1)*100,2) r1<-margin.table(t1, 1) # (summed over rows) c1<-margin.table(t1, 2) # (summed over columns) r1;c1 e1<-r1%*%t(c1)/sum(t1);e1 t2<-(t1-e1)^2/e1;t2;sum(t2) qchisq(.95, df = 1) 1-pchisq(sum(t2),(length(r1)-1)*(length(c1)-1))