From Mathematics to Generic Programming: The First Algorithm
- 2.1 Egyptian Multiplication
- 2.2 Improving the Algorithm
- 2.3 Thoughts on the Chapter
- Moses speedily learned arithmetic, and geometry.
- …This knowledge he derived from the Egyptians,
- who study mathematics above all things.
- Philo of Alexandria, Life of Moses
An algorithm is a terminating sequence of steps for accomplishing a computational task. Algorithms are so closely associated with the notion of computer programming that most people who know the term probably assume that the idea of algorithms comes from computer science. But algorithms have been around for literally thousands of years. Mathematics is full of algorithms, some of which we use every day. Even the method schoolchildren learn for long addition is an algorithm.
Despite its long history, the notion of an algorithm didn’t always exist; it had to be invented. While we don’t know when algorithms were first invented, we do know that some algorithms existed in Egypt at least as far back as 4000 years ago.
* * *
Ancient Egyptian civilization was centered on the Nile River, and its agriculture depended on the river’s floods to enrich the soil. The problem was that every time the Nile flooded, all the markers showing the boundaries of property were washed away. The Egyptians used ropes to measure distances, and developed procedures so they could go back to their written records and reconstruct the property boundaries. A select group of priests who had studied these mathematical techniques were responsible for this task; they became known as “rope-stretchers.” The Greeks would later call them geometers, meaning “Earth-measurers.”
Unfortunately, we have little written record of the Egyptians’ mathematical knowledge. Only two mathematical documents survived from this period. The one we are concerned with is called the Rhind Mathematical Papyrus, named after the 19th-century Scottish collector who bought it in Egypt. It is a document from about 1650 BC written by a scribe named Ahmes, which contains a series of arithmetic and geometry problems, together with some tables for computation. This scroll contains the first recorded algorithm, a technique for fast multiplication, along with a second one for fast division. Let’s begin by looking at the fast multiplication algorithm, which (as we shall see later in the book) is still an important computational technique today.
2.1 Egyptian Multiplication
The Egyptians’ number system, like that of all ancient civilizations, did not use positional notation and had no way to represent zero. As a result, multiplication was extremely difficult, and only a few trained experts knew how to do it. (Imagine doing multiplication on large numbers if you could only manipulate something like Roman numerals.)
How do we define multiplication? Informally, it’s “adding something to itself a number of times.” Formally, we can define multiplication by breaking it into two cases: multiplying by 1, and multiplying by a number larger than 1.
We define multiplication by 1 like this:
Equation 2.1
1a = a
Next we have the case where we want to compute a product of one more thing than we already computed. Some readers may recognize this as the process of induction; we’ll use that technique more formally later on.
Equation 2.1
(n + 1)a = na + a
One way to multiply n by a is to add instances of a together n times. However, this could be extremely tedious for large numbers, since n–1 additions are required. In C++, the algorithm looks like this:
int multiply0(int n, int a) {
if (n == 1) return a;
return multiply0(n -1, a) + a;
}
The two lines of code correspond to equations 2.1 and 2.2. Both a and n must be positive, as they were for the ancient Egyptians.
The algorithm described by Ahmes-which the ancient Greeks knew as "Egyptian multiplication" and which many modern authors refer to as the "Russian Peasant Algorithm"1- relies on the following insight:
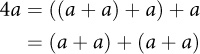
This optimization depends on the law of associativity of addition:
- a +(b + c)=(a + b)+ c
It allows us to compute a + a only once and reduce the number of additions.
The idea is to keep halving n and doubling a, constructing a sum of powerof-2 multiples. At the time, algorithms were not described in terms of variables such as a and n; instead, the author would give an example and then say, "Now do the same thing for other numbers." Ahmes was no exception; he demonstrated the algorithm by showing the following table for multiplying n = 41 by a = 59:
1 |
✓ |
59 |
2 |
118 |
|
4 |
236 |
|
8 |
✓ |
472 |
16 |
944 |
|
32 |
✓ |
1888 |
Each entry on the left is a power of 2; each entry on the right is the result of doubling the previous entry (since adding something to itself is relatively easy). The checked values correspond to the 1-bits in the binary representation of 41. The table basically says that
- 41 x 59 =(1 x 59)+(8 x 59)+(32 x 59)
where each of the products on the right can be computed by doubling 59 the correct number of times.
The algorithm needs to check whether n is even and odd, so we can infer that the Egyptians knew of this distinction, although we do not have direct proof. But ancient Greeks, who claimed that they learned their mathematics from the Egyptians, certainly did. Here’s how they defined2even and odd, expressed in modern notation:3
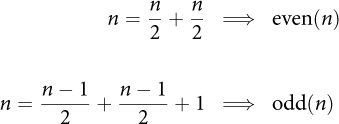
We will also rely on this requirement:
odd(n) ⇒ half(n) = half(n-1)
This is how we express the Egyptian multiplication algorithm in C++:
int multiply1(int n, int a) {
if (n == 1) return a;
int result = multiply1(half(n), a + a);
if (odd(n)) result = result + a;
return result;
}
We can easily implement odd(x) by testing the least significant bit of x, and half(x) by a single right shift of x:
bool odd(int n) { return n & 0x1; }
int half(int n) { return n >> 1; }
How many additions is multiply1 going to do? Every time we call the function, we'll need to do the addition indicated by the + in a + a. Since we are halving the value as we recurse, we'll invoke the function log n times.4 And some of the time, we'll need to do another addition indicated by the + in result + a. So the total number of additions will be
#+(n)= ⌊log n⌋ +(v(n) − 1)
where v(n) is the number of 1s in the binary representation of n (the population count or pop count). So we have reduced an O(n) algorithm to one that is O(log n).
Is this algorithm optimal? Not always. For example, if we want to multiply by 15, the preceding formula would give this result:
#+(15)= 3 + 4 − 1 = 6
But we can actually multiply by 15 with only 5 additions, using the following procedure:
int multiply_by_15(int a) {
int b = (a + a) + a; // b == 3*a
int c = b + b; // c == 6*a
return (c + c) + b; //12*a + 3*a
}
Such a sequence of additions is called an addition chain. Here we have discovered an optimal addition chain for 15. Nevertheless, Ahmes’s algorithm is good enough for most purposes.
Exercise 2.1. Find optimal addition chains for n < 100.
At some point the reader may have observed that some of these computations would be even faster if we first reversed the order of the arguments when the first is greater than the second (for example, we could compute 3 x 15 more easily than15x3). That’s true, and the Egyptians knew this. But we’re not going to add that optimization here, because as we’ll see in Chapter 7, we’re eventually going to want to generalize our algorithm to cases where the arguments have different types and the order of the arguments matters.