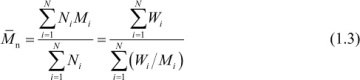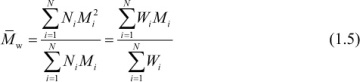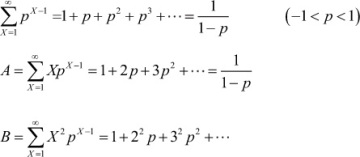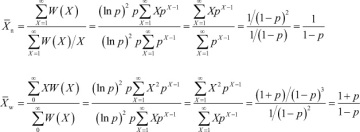This chapter is from the book
This chapter is from the book
This chapter is from the book
1.3 Molecular Weight
1.3.1 Molecular-Weight Distribution
A typical synthetic polymer sample contains chains with a wide distribution of chain lengths. This distribution is seldom symmetric and contains some molecules of very high molecular weight. A representative distribution is illustrated in Figure 1-8. The exact breadth of the molecular-weight distribution depends upon the specific conditions of polymerization, as will be described in Chapter 2. For example, the polymerization of some olefins can result in molecular-weight distributions that are extremely broad. In other polymerizations, polymers with very narrow molecular-weight distributions can be obtained. As will be shown in subsequent chapters, many polymer properties, such as melt viscosity, are dependent on molecular weight and molecular-weight distribution. Therefore, it is useful to define molecular-weight averages associated with a given molecular-weight distribution as detailed in this section.
)
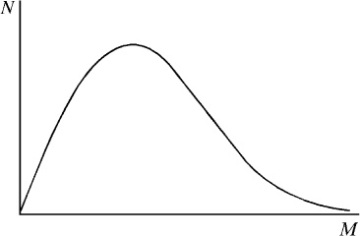
Figure 1-8 A representation of a continuous distribution of molecular weights shown as a plot of the number of moles of chains, N, having molecular weight M, against M.
1.3.2 Molecular-Weight Averages
For a discrete distribution of molecular weights, an average molecular weight,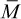 
, may be defined as
)
where Ni indicates the number of moles of molecules having a molecular weight of Mi and the parameter α is a weighting factor that defines a particular average of the molecular-weight distribution. The weight, Wi, of molecules with molecular weight Mi is then
)
Molecular weights that are important in determining polymer properties are the number-average,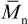 
(α = 1), the weight-average, 
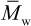(α = 2), and the z-average, 
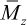(α = 3), molecular weights.
Since the molecular-weight distribution of commercial polymers is normally a continuous function, molecular-weight averages can be determined by integration if the appropriate mathematical form of the molecular-weight distribution (i.e., N as a function of M as illustrated in Figure 1-8) is known or can be approximated. Such mathematical forms include theoretical distribution functions derived on the basis of a statistical consideration of an idealized polymerization, such as the Flory, Schultz, Tung, and Pearson distributions 9 (see Example 1.1 and Problem 1.3) and standard probability functions, such as the Poisson and logarithmic-normal distributions.
It follows from eq. (1.1) that the number-average molecular weight for a discrete distribution of molecular weights is given as
)
where N is the total number of molecular-weight species in the distribution. The expression for the number-average molecular weight of a continuous distribution function is
)
The respective relationships for the weight-average molecular weight of a discrete and a continuous distribution are given by
)
and
)
In the case of high-molecular-weight polymers, the number-average molecular weight is directly determined by membrane osmometry, while the weight-average molecular weight is determined by light-scattering and other scattering techniques as described in Chapter 3. As mentioned earlier, a higher moment of the molecular-weight distribution is the z-average molecular weight (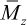) where α = 3. As discussed later in Chapter 3 (Section 3.3.3), a viscosity-average molecular weight, 
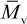, can be obtained from dilute-solution viscometry. The viscosity-average molecular weight falls between 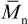and 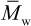depending upon whether the solvent is a good or poor solvent for the polymer. In the case of a good solvent, 
.
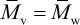A measure of the breadth of the molecular-weight distribution is given by the ratios of molecular-weight averages. For this purpose, the most commonly used ratio is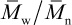 
, called the polydispersity index or PDI 9. Recent IUPAC recommendations suggest the use of the term molar-mass dispersity, DM, for this ratio 10. The PDIs of commercial polymers vary widely. For example, commercial grades of polystyrene with a 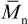of over 100,000 have polydispersity indices between 2 and 5, while polyethylene synthesized in the presence of a stereospecific catalyst may have a PDI as high as 30.* In contrast, the PDI of some vinyl polymers prepared by “living” polymerization (see Chapter 2) can be as low as 1.06. Such polymers with nearly monodisperse molecular-weight distributions are useful as molecular-weight standards for the determination of molecular weights and molecular-weight distributions of commercial polymers (see Section 3.3.4).
Example 1.1
A polydisperse sample of polystyrene is prepared by mixing three monodisperse samples in the following proportions:
1 g |
10,000 molecular weight |
2 g |
50,000 molecular weight |
2 g |
100,000 molecular weight |
Using this information, calculate the number-average molecular weight, weight-average molecular weight, and PDI of the mixture.
Solution
Using eqs. (1.3) and (1.5), we obtain the following:
)
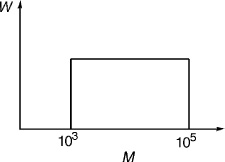
Example 1.2
A polymer is fractionated and is found to have the continuous molecular-weight distribution shown below as a plot of the weight, W, of molecules having molecular weight, M, versus M. Given this molecular-weight distribution, calculate 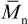and .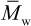
Solution
Using eqs. (1.4) and (1.6), we obtain the following:
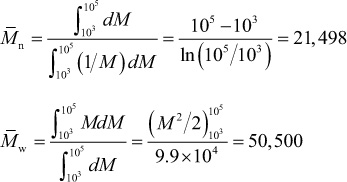
Example 1.3
The single-parameter Flory distribution is given as
W(X) = X(ln p)2 px
where X is the degree of polymerization and p is the fractional monomer conversion in a step-growth polymerization. Using this equation, obtain expressions for the number-average and weight-average degrees of polymerization* in terms of X and p.†
Solution
Using the following geometric series:
)
Since it can be shown that B(1 – p) = A(1 + p), it follows that
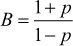, and then
)