MSD string sort
To implement a general-purpose string sort, where strings are not necessarily all the same length, we consider the characters in left-to-right order. We know that strings that start with a should appear before strings that start with b, and so forth. The natural way to implement this idea is a recursive method known as most-significant-digit-first (MSD) string sort. We use key-indexed counting to sort the strings according to their first character, then (recursively) sort the subarrays corresponding to each character (excluding the first character, which we know to be the same for each string in each subarray). Like quicksort, MSD string sort partitions the array into subarrays that can be sorted independently to complete the job, but it partitions the array into one subarray for each possible value of the first character, instead of the two or three partitions in quicksort.
Figure 5.8 Sorting a card deck with MSD string sort
End-of-string convention.
We need to pay particular attention to reaching the ends of strings in MSD string sort. For a proper sort, we need the subarray for strings whose characters have all been examined to appear as the first subarray, and we do not want to recursively sort this subarray. To facilitate these two parts of the computation we use a private two-argument toChar() method to convert from an indexed string character to an array index that returns -1 if the specified character position is past the end of the string. Then, we just add 1 to each returned value, to get a nonnegative int that we can use to index count[]. This convention means that we have R+1 different possible character values at each string position: 0 to signify end of string, 1 for the first alphabet character, 2 for the second alphabet character, and so forth. Since key-indexed counting already needs one extra position, we use the code int count[] = new int[R+2]; to create the array of frequency counts (and set all of its values to 0). Note: Some languages, notably C and C++, have a built-in end-of-string convention, so our code needs to be adjusted accordingly for such languages.

Figure 5.9 Overview of MSD string sort
With these preparations, the implementation of MSD string sort, in Algorithm 5.2, requires very little new code. We add a test to cutoff to insertion sort for small subarrays (using a specialized insertion sort that we will consider later), and we add a loop to key-indexed counting to do the recursive calls. As summarized in the table at the bottom of this page, the values in the count[] array (after serving to count the frequencies, transform counts to indices, and distribute the data) give us precisely the information that we need to (recursively) sort the subarrays corresponding to each character value.

Figure 5.10 Typical candidate for MSD string sort
Specified alphabet.
The cost of MSD string sort depends strongly on the number of possible characters in the alphabet. It is easy to modify our sort method to take an Alphabet as argument, to allow for improved efficiency in clients involving strings taken from relatively small alphabets. The following changes will do the job:
- Save the alphabet in an instance variable alpha in the constructor.
- Set R to alpha.R() in the constructor.
- Replace s.charAt(d) with alpha.toIndex(s.charAt(d)) in charAt().
In our running examples, we use strings made up of lowercase letters. It is also easy to extend LSD string sort to provide this feature, but typically with much less impact on performance than for MSD string sort.
|
at completion of phase for dth character |
value of count[r] is |
||||
|
r = 0 |
r = 1 |
r between 2 and R-1 |
r = R |
r = R+1 |
|
|
count frequencies |
0 (not used) |
number of strings of length d |
number of strings whose |
||
|
transform |
start index of subarray for strings of length d |
start index of subarray for strings whose |
not |
||
|
distribute |
start index of subarray for strings |
not |
|||
|
1 + end index of subarray for strings of length d |
1 + end index of subarray for strings whose dth character value is r-1 |
not |
|||
Interpretation of count[] values during MSD string sort
The code in Algorithm 5.2 is deceptively simple, masking a rather sophisticated computation. It is definitely worth your while to study the trace of the top level at the bottom of this page and the trace of recursive calls on the next page, to be sure that you understand the intricacies of the algorithm. This trace uses a cutoff-for-small-subarrays threshold value (M) of 0, so that you can see the sort to completion for this small example. The strings in this example are taken from Alphabet.LOWERCASE, with R = 26; bear in mind that typical applications might use Alphabet.EXTENDED.ASCII, with R = 256, or Alphabet.UNICODE, with R = 65536. For large alphabets, MSD string sort is so simple as to be dangerous—improperly used, it can consume outrageous amounts of time and space. Before considering performance characteristics in detail, we shall discuss three important issues (all of which we have considered before, in Chapter 2) that must be addressed in any application.
In our running examples, we use strings made up of lowercase letters. It is also easy to extend LSD string sort to provide this feature, but typically with much less impact on performance than for MSD string sort.
The code in Algorithm 5.2 is deceptively simple, masking a rather sophisticated computation. It is definitely worth your while to study the trace of the top level at the bottom of this page and the trace of recursive calls on the next page, to be sure that you understand the intricacies of the algorithm. This trace uses a cutoff-for-small-subarrays threshold value (M) of 0, so that you can see the sort to completion for this small example. The strings in this example are taken from Alphabet.LOWERCASE, with R = 26; bear in mind that typical applications might use Alphabet.EXTENDED_ASCII, with R = 256, or Alphabet.UNICODE16, with R = 65536. For large alphabets, MSD string sort is so simple as to be dangerous—improperly used, it can consume outrageous amounts of time and space. Before considering performance characteristics in detail, we shall discuss three important issues (all of which we have considered before, in Chapter 2) that must be addressed in any application.

Figure 5.11 Trace of MSD string sort: top level of sort(a, 0, 13, 0)
Small subarrays.
The basic idea behind MSD string sort is quite effective: in typical applications, the strings will be in order after examining only a few characters in the key. Put another way, the method quickly divides the array to be sorted into small subarrays. But this is a double-edged sword: we are certain to have to handle huge numbers of tiny subarrays, so we had better be sure that we handle them efficiently. Small subarrays are of critical importance in the performance of MSD string sort. We have seen this situation for other recursive sorts (quicksort and mergesort), but it is much more dramatic for MSD string sort. For example, suppose that you are sorting millions of ASCII strings (R = 256) that are all different, with no cutoff for small subarrays. Each string eventually finds its way to its own subarray, so you will sort millions of subarrays of size 1. But each such sort involves initializing the 258 entries of the count[] array to 0 and transforming them all to indices. This cost is likely to dominate the rest of the sort. With Unicode (R = 65536) the sort might be thousands of times slower. Indeed, many unsuspecting sort clients have seen their running times explode from minutes to hours on switching from ASCII to Unicode, for precisely this reason. Accordingly, the switch to insertion sort for small subarrays is a must for MSD string sort. To avoid the cost of reexamining characters that we know to be equal, we use the version of insertion sort given at the top of the page, which takes an extra argument d and assumes that the first d characters of all the strings to be sorted are known to be equal. The efficiency of this code depends on substring() being a constant-time operation. As with quicksort and mergesort, most of the benefit of this improvement is achieved with a small value of the cutoff, but the savings here are much more dramatic. The diagram at right shows the results of experiments where using a cutoff to insertion sort for subarrays of size 10 or less decreases the running time by a factor of 10 for a typical application.
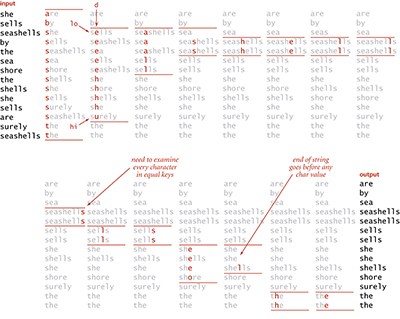
Figure 5.12 Trace of recursive calls for MSD string sort (no cutoff for small subarrays, subarrays of size 0 and 1 omitted)
public static void sort(String[] a, int lo, int hi, int d)
{ // Sort from a[lo] to a[hi], starting at the dth character.
for (int i = lo; i <= hi; i++)
for (int j = i; j > lo && less(a[j], a[j-1], d); j--)
exch(a, j, j-1);
}
private static boolean less(String v, String w, int d)
{ return v.substring(d).compareTo(w.substring(d)) < 0; }
Insertion sort for strings whose first d characters are equal
Equal keys.
A second pitfall for MSD string sort is that it can be relatively slow for subarrays containing large numbers of equal keys. If a substring occurs sufficiently often that the cutoff for small subarrays does not apply, then a recursive call is needed for every character in all of the equal keys. Moreover, key-indexed counting is an inefficient way to determine that the characters are all equal: not only does each character need to be examined and each string moved, but all the counts have to be initialized, converted to indices, and so forth. Thus, the worst case for MSD string sorting is when all keys are equal. The same problem arises when large numbers of keys have long common prefixes, a situation often found in applications.
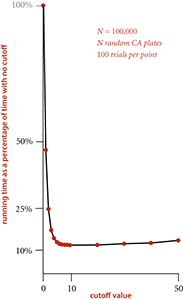
Figure 5.13 Effect of cutoff for small subarrays in MSD string sort
Extra space.
To do the partitioning, MSD uses two auxiliary arrays: the temporary array for distributing keys (aux[]) and the array that holds the counts that are transformed into partition indices (count[]). The aux[] array is of size N and can be created outside the recursive sort() method. This extra space can be eliminated by sacrificing stability (see Exercise 5.1.17), but it is often not a major concern in practical applications of MSD string sort. Space for the count[] array, on the other hand, can be an important issue (because it cannot be created outside the recursive sort() method) as addressed in Proposition D below.
Random string model.
To study the performance of MSD string sort, we use a random string model, where each string consists of (independently) random characters, with no bound on their length. Long equal keys are essentially ignored, because they are extremely unlikely. The behavior of MSD string sort in this model is similar to its behavior in a model where we consider random fixed-length keys and also to its performance for typical real data; in all three, MSD string sort tends to examine just a few characters at the beginning of each key, as we will see.

Figure 5.14 Characters examined by MSD string sort
Performance.
The running time of MSD string sort depends on the data. For compare-based methods, we were primarily concerned with the order of the keys; for MSD string sort, the order of the keys is immaterial, but we are concerned with the values of the keys.
- For random inputs, MSD string sort examines just enough characters to distinguish among the keys, and the running time is sublinear in the number of characters in the data (it examines a small fraction of the input characters).
- For nonrandom inputs, MSD string sort still could be sublinear but might need to examine more characters than in the random case, depending on the data. In particular, it has to examine all the characters in equla keys, so the running time is nearly linear in the number of characters in the data when significant numbers of equal keys are present.
- In the worst case, MSD string sort examines all the characters in the keys, so the running time is linear in the number of characters in the data (like LSD string sort). A worst-case input is one with all strings equal.
Some applications involve distinct keys that are well-modeled by the random string model; others have significant numbers of equal keys or long common prefixes, so the sort time is closer to the worst case. Our license-plate-processing application, for example, can fall anywhere between these extremes: if our engineer takes an hour of data from a busy interstate, there will not be many duplicates and the random model will apply; for a week’s worth of data on a local road, there will be numerous duplicates and performance will be closer to the worst case.
Proposition C. To sort N random strings from an R-character alphabet, MSD string sort examines about N log R N characters, on average.
Proof sketch: We expect the subarrays to be all about the same size, so the recurrence CN = RCN/R + N approximately describes the performance, which leads to the stated result, generalizing our argument for quicksort in Chapter 2. Again, this description of the situation is not entirely accurate, because N/R is not necessarily an integer, and the subarrays are the same size only on the average (and because the number of characters in real keys is finite). These effects turn out to be less significant for MSD string sort than for standard quicksort, so the leading term of the running time is the solution to this recurrence. The detailed analysis that proves this fact is a classical example in the analysis of algorithms, first done by Knuth in the early 1970s.
As food for thought and to indicate why the proof is beyond the scope of this book, note that key length does not play a role. Indeed, the random-string model allows key length to approach infinity. There is a nonzero probability that two keys will match for any specified number of characters, but this probability is so small as to not play a role in our performance estimates.
As we have discussed, the number of characters examined is not the full story for MSD string sort. We also have to take into account the time and space required to count frequencies and turn the counts into indices.
Proposition D. MSD string sort uses between 8N 1 3R and ~7wN 1 3WR array accesses to sort N strings taken from an R-character alphabet, where w is the average string length.
Proof: Immediate from the code, Proposition A, and Proposition B. In the best case MSD sort uses just one pass; in the worst case, it performs like LSD string sort.
When N is small, the factor of R dominates. Though precise analysis of the total cost becomes difficult and complicated, you can estimate the effect of this cost just by considering small subarrays when keys are distinct. With no cutoff for small subarrays, each key appears in its own subarray, so NR array accesses are needed for just these subarrays. If we cut off to small subarrays of size M, we have about N/M subarrays of size M, so we are trading off NR/M array accesses with NM/4 compares, which tells us that we should choose M to be proportional to the square root of R.
Proposition D (continued). To sort N strings taken from an R-character alphabet, the amount of space needed by MSD string sort is proportional to R times the length of the longest string (plus N ), in the worst case.
Proof: The count[] array must be created within sort(), so the total amount of space needed is proportional to R times the depth of recursion (plus N for the auxiliary array). Precisely, the depth of the recursion is the length of the longest string that is a prefix of two or more of the strings to be sorted.
As just discussed, equal keys cause the depth of the recursion to be proportional to the length of the keys. The immediate practical lesson to be drawn from Proposition D is that it is quite possible for MSD string sort to run out of time or space when sorting long strings taken from large alphabets, particularly if long equal keys are to be expected. For example, with Alphabet.UNICODE and more than M equal 1,000-character strings, MSD.sort() would require space for over 65 million counters!
The main challenge in getting maximum efficiency from MSD string sort on keys that are long strings is to deal with lack of randomness in the data. Typically, keys may have long stretches of equal data, or parts of them might fall in only a narrow range. For example, an information-processing application for student data might have keys that include graduation year (4 bytes, but one of four different values), state names (perhaps 10 bytes, but one of 50 different values), and gender (1 byte with one of two given values), as well as a person’s name (more similar to random strings, but probably not short, with nonuniform letter distributions, and with trailing blanks in a fixed-length field). Restrictions like these lead to large numbers of empty subarrays during the MSD string sort. Next, we consider a graceful way to adapt to such situations.

