- 2-1 Manipulating Rightmost Bits
- 2-2 Addition Combined with Logical Operations
- 2-3 Inequalities among Logical and Arithmetic Expressions
- 2-4 Absolute Value Function
- 2-5 Average of Two Integers
- 2-6 Sign Extension
- 2-7 Shift Right Signed from Unsigned
- 2-8 Sign Function
- 2-9 Three-Valued Compare Function
- 2-10 Transfer of Sign Function
- 2-11 Decoding a "Zero Means 2 **n" Field
- 2-12 Comparison Predicates
- 2-13 Overflow Detection
- 2-14 Condition Code Result of Add, Subtract, and Multiply
- 2-15 Rotate Shifts
- 2-16 Double-Length Add/Subtract
- 2-17 Double-Length Shifts
- 2-18 Multibyte Add, Subtract, Absolute Value
- 2-19 Doz, Max, Min
- 2-20 Exchanging Registers
- 2-21 Alternating among Two or More Values
- 2-22 A Boolean Decomposition Formula
- 2-23 Implementing Instructions for All 16 Binary Boolean Operations
This chapter is from the book
This chapter is from the book
This chapter is from the book
2–5 Average of Two Integers
The following formula can be used to compute the average of two unsigned integers, ⌊(x + y)/2⌋ without causing overflow [Dietz]:
)
The formula below computes ⌈(x + y)/2⌉ for unsigned integers:
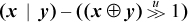
To compute the same quantities (“floor and ceiling averages”) for signed integers, use the same formulas, but with the unsigned shift replaced with a signed shift.
For signed integers, one might also want the average with the division by 2 rounded toward 0. Computing this “truncated average” (without causing overflow) is a little more difficult. It can be done by computing the floor average and then correcting it. The correction is to add 1 if, arithmetically, x + y is negative and odd. But x + y is negative if and only if the result of (3), with the unsigned shift replaced with a signed shift, is negative. This leads to the following method (seven instructions on the basic RISC, after commoning the subexpression x ⊕ y):
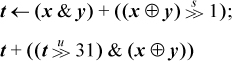
Some common special cases can be done more efficiently. If x and y are signed integers and known to be nonnegative, then the average can be computed as simply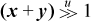 
. The sum can overflow, but the overflow bit is retained in the register that holds the sum, so that the unsigned shift moves the overflow bit to the proper position and supplies a zero sign bit.
If x and y are unsigned integers and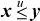 
, or if x and y are signed integers and x ≤ y (signed comparison), then the average is given by x + 
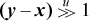. These are floor averages, for example, the average of −1 and 0 is −1.