- 2-1 Manipulating Rightmost Bits
- 2-2 Addition Combined with Logical Operations
- 2-3 Inequalities among Logical and Arithmetic Expressions
- 2-4 Absolute Value Function
- 2-5 Average of Two Integers
- 2-6 Sign Extension
- 2-7 Shift Right Signed from Unsigned
- 2-8 Sign Function
- 2-9 Three-Valued Compare Function
- 2-10 Transfer of Sign Function
- 2-11 Decoding a "Zero Means 2 **n" Field
- 2-12 Comparison Predicates
- 2-13 Overflow Detection
- 2-14 Condition Code Result of Add, Subtract, and Multiply
- 2-15 Rotate Shifts
- 2-16 Double-Length Add/Subtract
- 2-17 Double-Length Shifts
- 2-18 Multibyte Add, Subtract, Absolute Value
- 2-19 Doz, Max, Min
- 2-20 Exchanging Registers
- 2-21 Alternating among Two or More Values
- 2-22 A Boolean Decomposition Formula
- 2-23 Implementing Instructions for All 16 Binary Boolean Operations
This chapter is from the book
This chapter is from the book
This chapter is from the book
2–23 Implementing Instructions for All 16 Binary Boolean Operations
The instruction sets of some computers include all 16 binary Boolean operations. Many of the instructions are useless in that their function can be accomplished with another instruction. For example, the function f(x, y) = 0 simply clears a register, and most computers have a variety of ways to do that. Nevertheless, one reason a computer designer might choose to implement all 16 is that there is a simple and quite regular circuit for doing it.
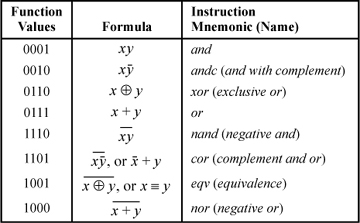
Refer to Table 2–1 on page 17, which shows all 16 binary Boolean functions. To implement these functions as instructions, choose four of the opcode bits to be the same as the function values shown in the table. Denoting these opcode bits by c0, c1, c2, and c3, reading from the bottom up in the table, and the input registers by x and y, the circuit for implementing all 16 binary Boolean operations is described by the logic expression
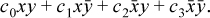
For example, with c0 = c1 = c2 = c3 = 0, the instruction computes the zero function, f(x, y) = 0. With c0 = 1 and the other opcode bits 0 it is the and instruction. With c0 = c3 = 0 and c1 = c2 = 1 it is exclusive or, and so forth.
This can be implemented with n 4:1 MUXs, where n is the word size of the machine. The data bits of x and y are the select lines, and the four opcode bits are the data inputs to each MUX. The MUX is a standard building block in today’s technology, and it is usually a very fast circuit. It is illustrated below.
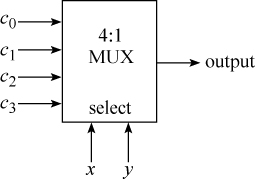
The function of the circuit is to select c0, c1, c2, or c3 to be the output, depending on whether x and y are 00, 01, 10, or 11, respectively. It is like a four-position rotary switch.
Elegant as this is, it is somewhat expensive in opcode points, using 16 of them. There are a number of ways to implement all 16 Boolean operations using only eight opcode points, at the expense of less regular logic. One such scheme is illustrated in Table 2–3.
Table 2-3. Eight Sufficient Boolean Instructions
)
The eight operations not shown in the table can be done with the eight instructions shown, by interchanging the inputs or by having both register fields of the instruction refer to the same register. See exercise 13.
IBM’s POWER architecture uses this scheme, with the minor difference that POWER has or with complement rather than complement and or. The scheme shown in Table 2–3 allows the last four instructions to be implemented by complementing the result of the first four instructions, respectively.
Historical Notes
The algebra of logic expounded in George Boole’s An Investigation of the Laws of Thought (1854) 7 is somewhat different from what we know today as “Boolean algebra.” Boole used the integers 1 and 0 to represent truth and falsity, respectively, and he showed how they could be manipulated with the methods of ordinary numerical algebra to formalize natural language statements involving “and,” “or,” and “except.” He also used ordinary algebra to formalize statements in set theory involving intersection, union of disjoint sets, and complementation. He also formalized statements in probability theory, in which the variables take on real number values from 0 to 1. The work often deals with questions of philosophy, religion, and law.
Boole is regarded as a great thinker about logic because he formalized it, allowing complex statements to be manipulated mechanically and flawlessly with the familiar methods of ordinary algebra.
Skipping ahead in history, there are a few programming languages that include all 16 Boolean operations. IBM’s PL/I (ca. 1966) includes a built-in function named BOOL. In BOOL(x, y, z), z is a bit string of length four (or converted to that if necessary), and x and y are bit strings of equal length (or converted to that if necessary). Argument z specifies the Boolean operation to be performed on x and y. Binary 0000 is the zero function, 0001 is xy, 0010 is x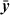
, and so forth.
Another such language is Basic for the Wang System 2200B computer (ca. 1974), which provides a version of BOOL that operates on character strings rather than on bit strings or integers [Neum].
Still another such language is MIT PDP-6 Lisp, later called MacLisp [GLS1].
Exercises
David de Kloet suggests the following code for the snoob function, for x ≠ 0, where the final assignment to y is the result:
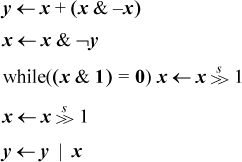
This is essentially the same as Gosper’s code (page 15), except the right shift is done with a while-loop rather than with a divide instruction. Because division is usually costly in time, this might be competitive with Gosper’s code if the while-loop is not executed too many times. Let n be the length of the bit strings x and y, k the number of 1-bits in the strings, and assume the code is executed for all values of x that have exactly k 1-bits. Then for each invocation of the function, how many times, on average, will the body of the while-loop be executed?
The text mentions that a left shift by a variable amount is not right-to-left computable. Consider the function x << (x & 1) [Knu8]. This is a left shift by a variable amount, but it can be computed by
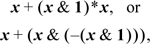
which are all right-to-left computable operations. What is going on here? Can you think of another such function?
Derive Dietz’s formula for the average of two unsigned integers,
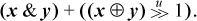
- Give an overflow-free method for computing the average of four unsigned integers, ⌊(a + b + c + d)/4⌋.
- Many of the comparison predicates shown on page 23 can be simplified substantially if bit 31 of either x or y is known. Show how the seven-instruction expression for
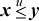can be simplified to three basic RISC, non-comparison, instructions if y31 = 0. - Show that if two numbers, possibly distinct, are added with “end-around carry,” the addition of the carry bit cannot generate another carry out of the high-order position.
- Show how end-around carry can be used to do addition if negative numbers are represented in one’s-complement notation. What is the maximum number of bit positions that a carry (from any bit position) might be propagated through?
- Show that the MUX operation, (x & m) | (y & ~m), can be done in three instructions on the basic RISC (which does not have the and with complement instruction).
- Show how to implement x ⊕ y in four instructions with and-or- not logic.
- Given a 32-bit word x and two integer variables i and j (in registers), show code to copy the bit of x at position i to position j. The values of i and j have no relation, but assume that 0 ≤ i, j ≤ 31.
- How many binary Boolean instructions are sufficient to evaluate any n-variable Boolean function if it is decomposed recursively by the method of the theorem?
- Show that alternative decompositions of Boolean functions of three variables are
(a) f(x, y, z) = g(x, y) ⊕
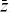h (x, y) (the “negative Davio decomposition”), and
(b) f(x, y, z) = g (x, y) ⊕ (z + h (x, y)). - It is mentioned in the text that all 16 binary Boolean operations can be done with the eight instructions shown in Table 2–3, by interchanging the inputs or by having both register fields of the instruction refer to the same register. Show how to do this.
- Suppose you are not concerned about the six Boolean functions that are really constants or unary functions, namely f(x, y) = 0, 1, x, y,
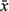, and 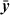, but you want your instruction set to compute the other ten functions with one instruction. Can this be done with fewer than eight binary Boolean instruction types (opcodes)? - Exercise 13 shows that eight instruction types suffice to compute any of the 16 two-operand Boolean operations with one R-R (register-register) instruction. Show that six instruction types suffice in the case of R-I (register-immediate) instructions. With R-I instructions, the input operands cannot be interchanged or equated, but the second input operand (the immediate field) can be complemented or, in fact, set to any value at no cost in execution time. Assume for simplicity that the immediate fields are the same length as the general purpose registers.
- Show that not all Boolean functions of three variables can be implemented with three binary logical instructions.