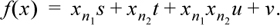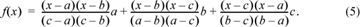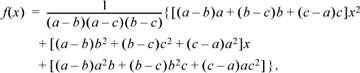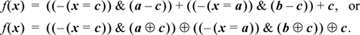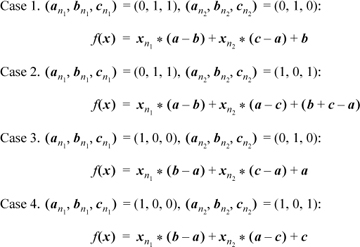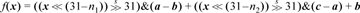- 2-1 Manipulating Rightmost Bits
- 2-2 Addition Combined with Logical Operations
- 2-3 Inequalities among Logical and Arithmetic Expressions
- 2-4 Absolute Value Function
- 2-5 Average of Two Integers
- 2-6 Sign Extension
- 2-7 Shift Right Signed from Unsigned
- 2-8 Sign Function
- 2-9 Three-Valued Compare Function
- 2-10 Transfer of Sign Function
- 2-11 Decoding a "Zero Means 2 **n" Field
- 2-12 Comparison Predicates
- 2-13 Overflow Detection
- 2-14 Condition Code Result of Add, Subtract, and Multiply
- 2-15 Rotate Shifts
- 2-16 Double-Length Add/Subtract
- 2-17 Double-Length Shifts
- 2-18 Multibyte Add, Subtract, Absolute Value
- 2-19 Doz, Max, Min
- 2-20 Exchanging Registers
- 2-21 Alternating among Two or More Values
- 2-22 A Boolean Decomposition Formula
- 2-23 Implementing Instructions for All 16 Binary Boolean Operations
2–21 Alternating among Two or More Values
Suppose a variable x can have only two possible values a and b, and you wish to assign to x the value other than its current one, and you wish your code to be independent of the values of a and b. For example, in a compiler x might be an opcode that is known to be either branch true or branch false, and whichever it is, you want to switch it to the other. The values of the opcodes branch true and branch false are arbitrary, probably defined by a C #define or enum declaration in a header file.
The straightforward code to do the switch is
if (x == a) x = b; else x = a;
or, as is often seen in C programs,
x = x == a ? b : a;
A far better (or at least more efficient) way to code it is either
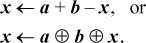
If a and b are constants, these require only one or two basic RISC instructions. Of course, overflow in calculating a + b can be ignored.
This raises the question: Is there some particularly efficient way to cycle among three or more values? That is, given three arbitrary but distinct constants a, b, and c, we seek an easy-to-evaluate function f that satisfies
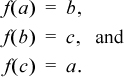
It is perhaps interesting to note that there is always a polynomial for such a function. For the case of three constants,
(The idea is that if x = a, the first and last terms vanish, and the middle term simplifies to b, and so on.) This requires 14 arithmetic operations to evaluate, and for arbitrary a, b, and c, the intermediate results exceed the computer’s word size. But it is just a quadratic; if written in the usual form for a polynomial and evaluated using Horner’s rule,5 it would require only five arithmetic operations (four for a quadratic with integer coefficients, plus one for a final division). Rearranging Equation (5) accordingly gives
This is getting too complicated to be interesting, or practical.
Another method, similar to Equation (5) in that just one of the three terms survives, is
f(x) = ((−(x = c)) & a) + ((−(x = a)) & b) + ((−(x = b)) & c).
This takes 11 instructions if the machine has the equal predicate, not counting loads of constants. Because the two addition operations are combining two 0 values with a nonzero, they can be replaced with or or exclusive or operations.
The formula can be simplified by precalculating a – c and b – c, and then using [GLS1]:
Each of these operations takes eight instructions, but on most machines these are probably no better than the straightforward C code shown below, which executes in four to six instructions for small a, b, and c.
if (x == a) x = b; else if (x == b) x = c; else x = a;
Pursuing this matter, there is an ingenious branch-free method of cycling among three values on machines that do not have comparison predicate instructions [GLS1]. It executes in eight instructions on most machines.
Because a, b, and c are distinct, there are two bit positions, n1 and n2, where the bits of a, b, and c are not all the same, and where the “odd one out” (the one whose bit differs in that position from the other two) is different in positions n1 and n2. This is illustrated below for the values 21, 31, and 20, shown in binary.
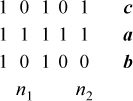
Without loss of generality, rename a, b, and c so that a has the odd one out in position n1 and b has the odd one out in position n2, as shown above. Then there are two possibilities for the values of the bits at position n1, namely (an1, bn1, cn1) = (0, 1, 1) or (1, 0, 0). Similarly, there are two possibilities for the bits at position n2, namely (an2, bn2, cn2) = (0, 1, 0) or (1, 0, 1). This makes four cases in all, and formulas for each of these cases are shown below.
In these formulas, the left operand of each multiplication is a single bit. A multiplication by 0 or 1 can be converted into an and with a value of 0 or all 1’s. Thus, the formulas can be rewritten as illustrated below for the first formula.
Because all variables except x are constants, this can be evaluated in eight instructions on the basic RISC. Here again, the additions and subtractions can be replaced with exclusive or.
This idea can be extended to cycling among four or more constants. The essence of the idea is to find bit positions n1, n2, …, at which the bits uniquely identify the constants. For four constants, three bit positions always suffice. Then (for four constants) solve the following equation for s, t, u, and v (that is, solve the system of four linear equations in which f(x) is a, b, c, or d, and the coefficients xni are 0 or 1):
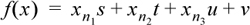
If the four constants are uniquely identified by only two bit positions, the equation to solve is