- 2-1 Manipulating Rightmost Bits
- 2-2 Addition Combined with Logical Operations
- 2-3 Inequalities among Logical and Arithmetic Expressions
- 2-4 Absolute Value Function
- 2-5 Average of Two Integers
- 2-6 Sign Extension
- 2-7 Shift Right Signed from Unsigned
- 2-8 Sign Function
- 2-9 Three-Valued Compare Function
- 2-10 Transfer of Sign Function
- 2-11 Decoding a "Zero Means 2 **n" Field
- 2-12 Comparison Predicates
- 2-13 Overflow Detection
- 2-14 Condition Code Result of Add, Subtract, and Multiply
- 2-15 Rotate Shifts
- 2-16 Double-Length Add/Subtract
- 2-17 Double-Length Shifts
- 2-18 Multibyte Add, Subtract, Absolute Value
- 2-19 Doz, Max, Min
- 2-20 Exchanging Registers
- 2-21 Alternating among Two or More Values
- 2-22 A Boolean Decomposition Formula
- 2-23 Implementing Instructions for All 16 Binary Boolean Operations
This chapter is from the book
This chapter is from the book
This chapter is from the book
2–2 Addition Combined with Logical Operations
We assume the reader is familiar with the elementary identities of ordinary algebra and Boolean algebra. Below is a selection of similar identities involving addition and subtraction combined with logical operations.
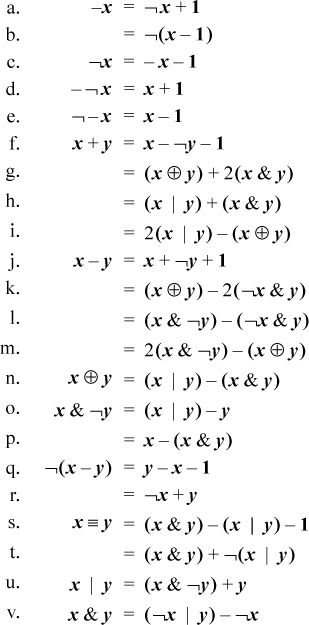
Equation (d) can be applied to itself repeatedly, giving –¬–¬x = x + 2, and so on. Similarly, from (e) we have ¬–¬– x = x – 2. So we can add or subtract any constant using only the two forms of complementation.
Equation (f) is the dual of (j), where (j) is the well-known relation that shows how to build a subtracter from an adder.
Equations (g) and (h) are from HAKMEM memo [HAK, item 23]. Equation (g) forms a sum by first computing the sum with carries ignored (x ⊕ y), and then adding in the carries. Equation (h) is simply modifying the addition operands so that the combination 0 + 1 never occurs at any bit position; it is replaced with 1 + 0.
It can be shown that in the ordinary addition of binary numbers with each bit independently equally likely to be 0 or 1, a carry occurs at each position with probability about 0.5. However, for an adder built by preconditioning the inputs using (g), the probability is about 0.25. This observation is probably not of value in building an adder, because for that purpose the important characteristic is the maximum number of logic circuits the carry must pass through, and using (g) reduces the number of stages the carry propagates through by only one.
Equations (k) and (l) are duals of (g) and (h), for subtraction. That is, (k) has the interpretation of first forming the difference ignoring the borrows (x ⊕ y), and then subtracting the borrows. Similarly, Equation (l) is simply modifying the subtraction operands so that the combination 1 – 1 never occurs at any bit position; it is replaced with 0 – 0.
Equation (n) shows how to implement exclusive or in only three instructions on a basic RISC. Using only and-or-not logic requires four instructions ((x | y) & ¬(x & y)). Similarly, (u) and (v) show how to implement and and or in three other elementary instructions, whereas using DeMorgan’s laws requires four.