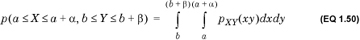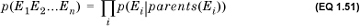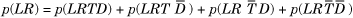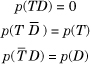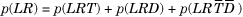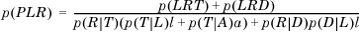This chapter is from the book
This chapter is from the book
This chapter is from the book
1.8. Jointly Distributed Random Variables
So far, we have considered distributions of one random variable. We now consider the distribution of two random variables simultaneously.
We call the distribution of X alone as the marginal distribution of X and denote it pX. Similarly, the marginal distribution of Y is denoted pY. Generalizing from the preceding example, we see that to obtain the marginal distribution of X, we should set X to each value in its domain and then sum over all possible values of Y. Similarly, to obtain the marginal distribution of Y, we set Y to each value in its domain and sum over all possible values of X.
An important special case of a joint distribution is when the two variables X and Y are independent. Then, pXY(xy) = p(X = x AND Y = y) = p(X = x) * p(Y = y) = pX(x)pY(y). That is, each entry in the joint distribution is obtained simply as the product of the marginal distributions corresponding to that value. We sometimes denote this as = pX(x)pY(y).
Given the joint distribution, we define the conditional probability mass function of X, denoted by pX|Y(x|y) by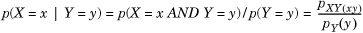 
.
We can generalize the notion of joint probability in three ways. We outline these generalizations next. Note that the concepts we have developed for the simple preceding case continue to hold for these generalizations.
- Instead of having only two values, 0 and 1, X and Y could assume any number of finite discrete values. In this case, if there are n values of X and m values of Y, we would need to specify, for the joint distribution, a total of nm values. If X and Y are independent, however, we need to specify only n + m values to completely specify the joint distribution.
- We can generalize this further and allow X and Y to be continuous random variables. Then, the joint probability distribution pXY(xy) is implicitly defined by
Intuitively, this is the probability that a randomly chosen two-dimensional vector will be in the vicinity of (a,b).
- As a further generalization, consider the joint distribution of n random variables, X1, X2,..., Xn, where each variable is either discrete or continuous. If they are all discrete, we need to define the probability of each possible choice of each value of Xi. This grows exponentially with the number of random variables and with the size of each domain of each random variable. Thus, it is impractical to completely specify the joint probability distribution for a large number of variables. Instead, we exploit pairwise independence between the variables, using the construct of a Bayesian network, which is described next.
)
1.8.1. Bayesian Networks
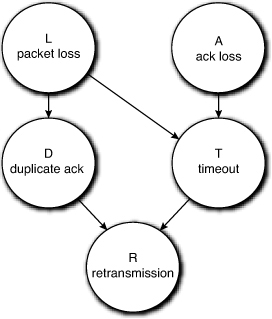
Bayes’s rule allows us to compute the degree to which one of a set of mutually exclusive prior events contributes to a posterior condition. Suppose that the posterior condition was itself a prior to yet another posterior, and so on. We could then imagine tracing this chain of conditional causation back from the final condition to the initial causes. This, in essence, is a Bayesian network. We will study one of the simplest forms of a Bayesian network next.
A Bayesian network with n nodes is a directed acyclic graph whose vertices represent random variables and whose edges represent conditional causation between these random variables: There is an edge from a random variable Ei, called the parent, or cause, to every random variable Ej whose outcome depends on it, called its children, or effects. If there is no edge between Ei and Ej, they are independent.
Each node in the Bayesian network stores the conditional probability distribution p(Ej|parents(Ej)), also called its local distribution. Note that if the node has no parents, its distribution is unconditionally known. The network allows us to compute the joint probability p(E1E2...En) as
)
That is, the joint distribution is simply the product of the local distributions. This greatly reduces the amount of information required to describe the joint probability distribution of the random variables. Choosing the Bayesian graph is a nontrivial problem and one that we will not discuss further. An overview can be found in the text by Russell and Norvig cited in Sections 1.9.
Note that, because the Bayesian network encodes the full joint distribution, we can in principle extract any probability we want from it. Usually, we want to compute something much simpler. A Bayesian network allows us to compute probabilities of interest without having to compute the entire joint distribution, as the next example demonstrates.
Example 1.42. Bayesian network
Consider the Bayesian network in Figure 1.10. Each circle shows a discrete random variable that can assume only two values: true or false. Each random variable is associated with an underlying event in the appropriate sample space, as shown in the figure. The network shows that if L, the random variable representing packet loss event, has the value true (the cause), this may lead to a timeout event at the TCP transmitter (effect), so that the random variable representing this T, has a higher probability of having the value true. Similarly, the random variable denoting the loss of an acknowledgment packet may also increase the probability that T assumes the value true. The node marked T, therefore, stores the probabilty that it assumes the value true conditional on the parents, assuming the set of values {(true, true), (true, false), (false, true), (false, false)}.
){kind=link}
Figure 1.10. A Bayesian network to represent TCP retransmissions
The network also represents the fact that a packet loss event affects the likelihood of a duplicate acknowledgment event. However, packet and ack loss events are mutually exclusive, as are duplicate acks and timeouts. Finally, if there is either a duplicate ack or a timeout at the transmitter, it will surely retransmit a packet.
The joint distribution of the random variables (L, A, D, T, R) would assign a probability to every possible combination of the variables, such as p(packet loss AND no ack loss AND no duplicate ack AND timeout AND no retransmission). In practice, we rarely need the joint distribution. Instead, we may be interested only in computing the following probability: p(packet loss | retransmission) = p(L|R). That is, we observe the event that the transmitter has retransmitted a packet. What is the probability that the event packet loss occurred: What is p(L|R)?
For notational simplicity, let p(R = true) = p(R) = r, p(L = true) = p(L) = l, p(T = true) = p(T) = t, p(A = true) = p(A) = a and p(D = true) = p(D) = d. From the network, it is clear that we can write p(R) as p(R|T)t + p(R|D)d. Similarly, t = p(T|L)l + p(T|A)a and d = p(D|L)l. Therefore,
- p(R) = r = p(R|T)(p(T|L)l + p(T|A)a) + p(R|D)p(D|L)l
If we know a and l and the conditional probabilities stored at each node, we can therefore compute r.
From the definition of conditional probabilities:
We have already seen how to compute the denominator. To compute the numerator, we sum across all possibilities for L and R as follows:
where the overbar represents the probability that the random variable assumes the value false. However, note that T and D are mutually exclusive, so
Thus,
The last term is 0 because we do not have a retransmission unless there is either a timeout or a duplicate ack. Thus, p(LR) = P(LRT) + P(LRD).
Replacing this in Equation 1.52, we get
All these variables can be computed by observations over sufficiently long durations of time. For instance, to compute p (LRT), we can compute the ratio of all retransmissions where there was both a packet loss and timeout event to the number of transmissions. Similarly, to compute p(R|T), we can compute the ratio of the number of times a retransmission happens due to a timeout to the number of times a timeout happens. This allows us to compute p(L|R) in practice.