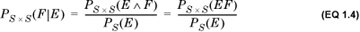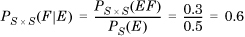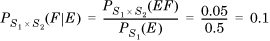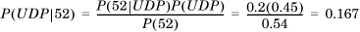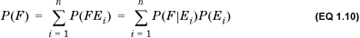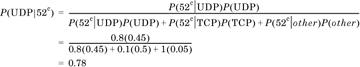1.2. Joint and Conditional Probability
Thus far, we have defined the terms used in studying probability and considered single events in isolation. Having set this foundation, we now turn our attention to the interesting issues that arise when studying sequences of events. In doing so, it is very important to keep track of the sample space in which the events are defined: A common mistake is to ignore the fact that two events in a sequence may be defined on different sample spaces.
1.2.1. Joint Probability
Consider two processes with sample spaces S1 and S2 that occur one after the other. The two processes can be viewed as a single joint process whose outcomes are the tuples chosen from the product space S1 × S2. We refer to the subsets of the product space as joint events. Just as before, we can associate probabilities with outcomes and events in the product space. To keep things straight, in this section, we denote the sample space associated with a probability as a subscript, so that PS1(E) denotes the probability of event E defined over sample space S1, and PS1 × S2 (E) is an event defined over the product space S1 × S2.
We will return to the topic of joint processes in Sections 1.8. We now turn our attention to the concept of conditional probability.
1.2.2. Conditional Probability
Common experience tells us that if a sky is sunny, there is no chance of rain in the immediate future but that if the sky is cloudy, it may or may not rain soon. Knowing that the sky is cloudy, therefore, increases the chance that it may rain soon, compared to the situation when it is sunny. How can we formalize this intuition?
To keep things simple, first consider the case when two events E and F share a common sample space and occur one after the other. Suppose that the probability of E is PS(E) and the probability of F is PS (F). Now, suppose that we are informed that event E actually occurred. By definition, the conditional probability of the event F conditioned on the occurrence of event E is denoted PS × S(F|E) (read “the probability of F given E”) and computed as
If knowing that E occurred does not affect the probability of F, E and F are said to be independent and
PS × S (EF) = PS(E)PS(F)
The notion of conditional probability generalizes to the case in which events are defined on more than one sample space. Consider a sequence of two processes with sample spaces S1 and S2 that occur one after the other. (This could be the condition of the sky now, for instance, and whether it rains after 2 hours.) Let event E be a subset of S1 and event F a subset of S2. Suppose that the probability of E is PS1(E) and the probability of F is PS2(F). Now, suppose that we are informed that event E occurred. We define the probability PS1 × S2 (F|E) as the conditional probability of the event F conditional on the occurrence of E as
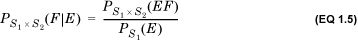
If knowing that E occurred does not affect the probability of F, E and F are said to be independent and
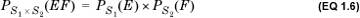
It is important not to confuse P(F|E) and P(F). The conditional probability is defined in the product space S1 × S2 and the unconditional probability in the space S2. Explicitly keeping track of the underlying sample space can help avoid apparent contradictions such as the one discussed in Example 1.14.
1.2.3. Bayes’s Rule
One of the most widely used rules in the theory of probability is due to an English country minister: Thomas Bayes. Its significance is that it allows us to infer “backwards” from effects to causes rather than from causes to effects. The derivation of his rule is straightforward, though its implications are profound.
We begin with the definition of conditional probability (Equation 1.4):
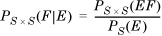
If the underlying sample spaces can be assumed to be implicitly known, we can rewrite this as

We interpret this to mean that the probability that both E and F occur is the product of the probabilities of two events: first, that E occurs; second, that conditional on E, F occurs.
Recall that P(F|E) is defined in terms of the event F following event E. Now, consider the converse: F is known to have occurred. What is the probability that E occurred? This is similar to the problem: If there is fire, there is smoke, but if we see smoke, what is the probability that it was due to a fire? The probability we want is P(E|F). Using the definition of conditional probability, it is given by

Substituting for P(F) from Equation 1.7, we get

which is Bayes’s rule. One way of interpreting this is that it allows us to compute the degree to which some effect, or posterior F, can be attributed to some cause, or prior E.
We can generalize Bayes’s rule when a posterior can be attributed to more than one prior. Consider a posterior F that is due to some set of n priors Ei such that the priors are mutually exclusive and exhaustive: That is, at least one of them occurs, and only one of them can occur. This implies that 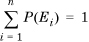 . Then,
. Then,
This is also called the law of total probability.
The law of total probability allows one further generalization of Bayes’s rule to obtain Bayes’s theorem. From the definition of conditional probability, we have
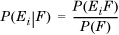
From Equation 1.7, we have
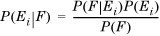
Substituting Equation 1.10, we get
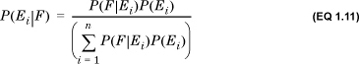
This is called the generalized Bayes’s rule, or Bayes’s theorem. It allows us to compute the probability of any one of the priors Ei, conditional on the occurrence of the posterior F. This is often interpreted as follows: We have some set of mutually exclusive and exhaustive hypotheses Ei. We conduct an experiment, whose outcome is F. We can then use Bayes’s formula to compute the revised estimate for each hypothesis.
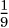 . Let E = {1,2} be an event in S1 and F = {b} be an event in S2. Then, the event EF is given by the tuples {(1, b), (2, b)} and has probability
. Let E = {1,2} be an event in S1 and F = {b} be an event in S2. Then, the event EF is given by the tuples {(1, b), (2, b)} and has probability 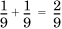 .
.