- Getting a Feel for Your Attributes
- Determining the Granularity for Numbers
- The Tension Trick
- Searching for the Right Numbers
- Further Steps
Determining the Granularity for Numbers
After you come up with attributes for game objects, you need to assign numbers to the attributes. Because you are making up all the attributes and numbers for your game, technically you could use any numbers you want. The granularity of the numbers you use can have a dramatic impact on how a player perceives the game. The following sections provide some to help you determine the granularity of your numbers.
Numbers Should Relate to Probability
Numbers should have a visible impact on the game. The larger the possible outcome of a random event, the larger the corresponding numbers of the game must be. For example, if a character has 10 HP, it doesn’t matter if the character receives 11 damage or 5,000 damage, as either one will be a one-hit kill. Say that you know a character is rolling 1D6 (a single six-sided die) for damage, and you always want the character to survive at least three hits. In this case, the minimum hit point value would be 111.
Let’s consider backgammon as an example. (Do a search for “official backgammon rules” if you need to familiarize yourself.) In backgammon, the maximum number of moves a piece can take at one time is 24. The maximum is 24 because even the largest roll possible can have a use and not be wasted. In addition, 24 is the number of spaces on the board (see Figure 11.1). The relationships between the number of needed movement spaces and the potential outcomes of the dice are intertwined. If you were to expand the board, you would likely need larger potential rolls to keep the game moving. Conversely, if you were to shrink the board, you would want to reduce the amount of possible movement.

Figure 11-1 Backgammon board
Some Numbers Need to Relate to Real-World Measurements
Some numbers, such as height, weight, and speed, are analogs of the real world. The scale of those numbers has already been decided for you. Even if it is better for your game to use three-digit numbers than to use smaller numbers, you can’t decide that every person in your game is going to be measured in hundreds of feet (or meters) in height. Players have incoming knowledge of fixed scales and expect you to play along with the real world. So, if being taller in your game is better, then you will need to adjust your scale. There are a few ways to do this:
Use a smaller unit of measurement so you get larger numbers.
Adjust your scale of numbers to fit a fixed attribute.
Convert the real-world scale to a game scale.
For example, you might list attributes for a basketball player as follows:
Example 1
Strength: 150
Height: 6 (feet)
Speed: 220
Dexterity: 180
This looks odd because the height attribute is a single digit, while the rest of the attributes are triple-digit numbers. In addition to looking odd, this would create the need to use fractions or decimals. Here’s another example of attributes for a basketball player:
Example 2
Strength: 150
Height: 182 (centimeters)
Speed: 220
Dexterity: 180
This scale is much better. All the attribute numbers are triple-digit numbers and within a similar range.
Here’s another example of attributes for a basketball player:
Example 3
Strength: 50
Height: 72 (inches)
Speed: 73
Dexterity: 60
This scale is also better than the first one. Changing to a more granular measurement of inches and switching all attributes to be two-digit numbers makes them line up nicely.
Now consider this final example of attributes for a basketball player:
Example 4
Strength: 150
Height: 165 (game units)
Speed: 220
Dexterity: 180
This scale also works because you have ditched reality and made your own scale that enables the attributes to all be three-digit numbers in a similar range. Making up your own units may lead to a bit of confusion as a player won’t initially know how to picture a height of 165 game units, but you can overcome this difficulty with art.
User Smaller Numbers for Easier Calculations
A player needs clear numbers for each individual calculation and for repeated calculations. If you are asking players to do calculations in their head in the game, then you need to limit the complexity of the numbers. Further, if you are asking players to do many calculations or frequently recurring calculations, you need to further restrict the complexity of those calculations. It is easiest for players to process simple numbers—that is, small whole numbers.
In very old games, attribute numbers are all very small. The number of pieces a player has, the faces of the dice, and total points for a game tend to be no more than two digits. Often they are single digits. Old games use small whole numbers to make the numbers easier for players to remember and use in calculations in their heads. The more frequently a player is required to do calculations, the simpler the calculations tend to be and the smaller the numbers involved are.
Think again about backgammon, for example. Players need to be able to calculate rolls and results in their heads, and complex systems of multiplication or addition would cause unneeded confusion. For each turn in backgammon, a player rolls 2D6 to determine how much movement their pieces get for that turn. A player gets double that movement with a roll of doubles. (Rolling double 6s, for example, allows the player to move a total of 24 spaces.) On every turn, the player uses the individual rolls of the dice, or adds together the rolls of two six-sided dice, and turns go by in a matter of seconds. Fortunately, adding together the rolls of two six-sided dice is a very easy calculation and does not slow the pace of the game. In addition, the results are all small numbers. The results also tie into the physical space of the game. The board contains only 24 spaces, so any more movement than that would be useless.
Let’s now consider scoring in the game spades. Spades has a rather sophisticated scoring system, where players guess their score at the beginning of the game and then, at the end of the game, compare their final results to their initial guess. They then use a scoring system to interpret their results and calculate the final score. This is a somewhat complex calculation, and players often use paper or a calculator to do the scoring—but it is only done once during a game. The numeric results are also much larger than in backgammon, with scores in the hundreds or even up over 1,000. Because this calculation occurs only once a game, it’s an event and can even build some tension as a game is calculated, but if it were done every turn, it would completely bog down the game.
Early and even many modern tabletop games and pen-and-paper RPGs continue to use attribute numbers in the single digits and low double digits. For example, a sample fifth edition Dungeons & Dragons character could start with the following attribute scores:
STR 10 DEX 13 CON 14 WIS 19 CHA 14
Note that all of these numbers are in the low two-digit range. Also, while this is a modern, fairly sophisticated game, it is working under the same limitations as backgammon in that the players are needing to do calculations in their head. Whereas in backgammon, players do calculations every few seconds, in an RPG they do calculations every few minutes.
As you can see from these examples, the less frequently calculations are made, the more complex they can be and the larger the numbers involved can be. When assigning numbers to attributes, you should think about how much calculation you expect your players to do in their heads. The more calculations, the smaller the numbers should be for attributes. The more frequent the calculations, the smaller and simpler the calculation and numbers must be.
Use Larger Numbers for More Granularity
If small numbers are easier for players to understand, why not use single-digit numbers for everything? Small numbers do not allow for much granularity or variety. Say that you are assigning strength to five fantasy characters. These are the five characters, and the feeling you want to convey through the strength attribute for each of them:
Human: Middle-of-the-road guy
Ogre: Much stronger than anyone else
Ork: Stronger than humans but significantly weaker than ogres
Goblin: Weakest by far, but not so weak that they can be ignored
Dwarf: Stronger than humans but notably weaker than orks
Here’s how you might turn these feelings into numbers if you want to constrain the numbers to 10 and below:
Human: Middle of the road leads you to choose the halfway point, which is 5.
Ogre: Because this is the strongest character, it is 10. Note that there is no longer room on the scale for stronger characters like dragons or giants. While this might be fine within the scope of your game, it does limit your ability to expand the game.
Ork: You might assign an ork a strength of 7 because an ork is much weaker than an ogre but is not that much stronger than a human.
Goblin: A goblin is the weakest character, so you assign it 2, but 2 might be too weak.
Dwarf: You are now stuck. If you assigned a dwarf 6, then this character would be stronger than a human but not notably weaker than an ork.
As you can see, even with just five characters and a few criteria, you start running out of space in the scale to properly translate your feelings about character strengths into numbers. As you add more characters and more criteria, the scale will get even more crowded, and characters will start to feel too similar. To fix this, it is tempting to make all the values considerably larger, allowing more granularity to work with.
Very Large Numbers Are Confusing
Given the problems discussed so far with small numbers, it might seem like a good idea to go to the opposite extreme in a computer game. If you were to use four- or five-digit numbers, you would have plenty of space to make a large variety without ever crowding your range. Further, given that the computer will be doing all the calculations, you don’t need to worry about players doing lots of math on big numbers, as they would need to do with a board game. But calculations are not limited to just what a player must do to make the game progress; they also tie in to how well the player can understand what is going on in the game. We humans are, in general, not designed to calculate large numbers in our heads. For example, try to calculate the final hit point score for each of the following scenarios in your head:
5 hit points, taking 2 points of damage
100 hit points, taking 27 points of damage
34863298 hit points, taking 456321 points of damage
It’s clear that the smaller the numbers, the easier the calculations.
The takeaway is that you need to find the right amount of granularity for your game. In general, you want to use numbers that are just large enough to accommodate all needed variety but no larger than absolutely necessary.
Humans Hate Decimals and Fractions, but Computers Don’t Mind Them
It is exceedingly rare, outside of educational math games, to ever show a player a decimal score or a fraction. It’s not that they aren’t valid numbers, but people just don’t like seeing or (worse) calculating them. Games typically show players only whole numbers.
However, behind the scenes, computers have absolutely no problem calculating decimals. This means you can feel free to use as many decimal places as you want for computer calculations as long as you can present whole (rounded) numbers to the player in a way that is not confusing.
Numbering Example
Figure 11.2 provides an example in which each column presents a pair of values: one for Attribute A and one for Attribute B. In each pair, the ratio of A to B is the same: 94%. Because each pair has the same ratio, for a computer, they would all work exactly the same way. However, players would be able to comprehend some of these numbers easily and others with great difficulty. If the players are going to see the numbers, you should use just the two-digit numbers, if possible, or the three-digit ones.
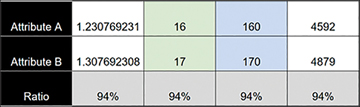
Figure 11-2 Number granularity example
