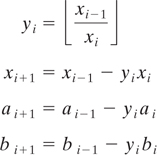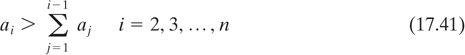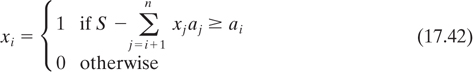This chapter is from the book
This chapter is from the book
This chapter is from the book
17.5 Public Key Cryptosystems
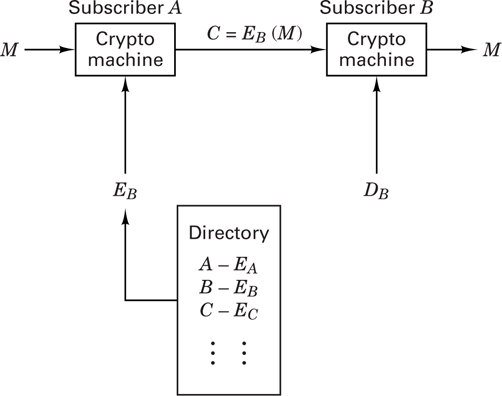
The concept of public key cryptosystems was introduced in 1976 by Diffie and Hellman [12]. In conventional cryptosystems the encryption algorithm can be revealed since the security of the system depends on a safeguarded key. The same key is used for both encryption and decryption. Public key cryptosystems utilize two different keys, one for encryption and the other for decryption. In public key cryptosystems, not only the encryption algorithm but also the encryption key can be publicly revealed without compromising the security of the system. In fact, a public directory, much like a telephone directory, is envisioned, which contains the encryption keys of all the subscribers. Only the decryption keys are kept secret. Figure 17.17 illustrates such a system. The important features of a public key cryptosystem are as follows:
)
The encryption algorithm EK and the decryption algorithm DK are invertible transformations on the plaintext M, or the ciphertext C, defined by the key K. That is, for each K and M, if C = EK(M), then M = DK(C) = DK[EK(M)].
For each K, EK and DK are easy to compute.
For each K, the computation of DK from EK is computationally intractable.
Such a system would enable secure communication between subscribers who have never met or communicated before. For example, as seen in Figure 17.17, subscriber A can send a message, M, to subscriber B by looking up B’s encryption key in the directory and applying the encryption algorithm, EB, to obtain the ciphertext C = EB(M), which he transmits on the public channel. Subscriber B is the only party who can decrypt C by applying his decryption algorithm, DB, to obtain M = DB(C).
17.5.1 Signature Authentication Using a Public Key Cryptosystem
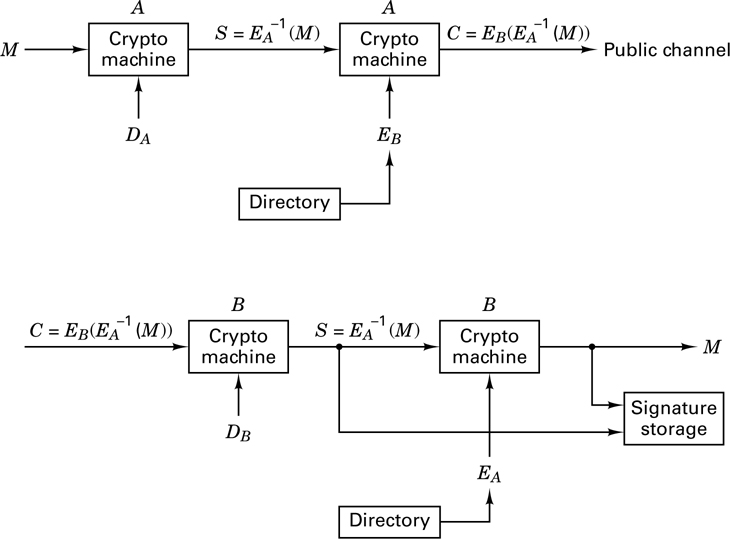
Figure 17.18 illustrates the use of a public key cryptosystem for signature authentication. Subscriber A “signs” his message by first applying his decryption algorithm, DA, to the message, yielding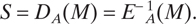 
. Next, he uses the encryption algorithm, EB, of subscriber B to encrypt S, yielding 
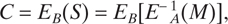, which he transmits on a public channel. When subscriber B receives C, he first decrypts it using his private decryption algorithm, DB, yielding 
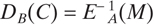. Then he applies the encryption algorithm of subscriber A to produce 
.
)
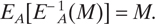If the result is an intelligible message, it must have been initiated by subscriber A, since no one else could have known A’s secret decryption key to form S = DA(M). Notice that S is both message dependent and signer dependent, which means that while B can be sure that the received message indeed came from A, at the same time A can be sure that no one can attribute any false messages to him.
17.5.2 A Trapdoor One-Way Function
Public key cryptosystems are based on the concept of trapdoor one-way functions. Let us first define a one-way function as an easily computed function whose inverse is computationally infeasible to find. For example, consider the function y = x5 + 12x3 + 107x + 123. It should be apparent that given x, y is easy to compute, but given y, x is relatively difficult to compute. A trapdoor one-way function is a one-way function whose inverse is easily computed if certain features, used to design the function, are known. Like a trapdoor, such functions are easy to go through in one direction. Without special information the reverse process takes an impossibly long time. We will apply the concept of a trapdoor in Section 17.5.5, when we discuss the Merkle–Hellman scheme.
17.5.3 The Rivest–Shamir–Adelman Scheme
In the Rivest–Shamir–Adelman (RSA) scheme, messages are first represented as integers in the range (0, n − 1). Each user chooses his own value of n and another pair of positive integers e and d, in a manner to be described below. The user places his encryption key, the number pair (n, e), in the public directory. The decryption key consists of the number pair (n, d), of which d is kept secret. Encryption of a message M and decryption of a ciphertext C are defined as follows:
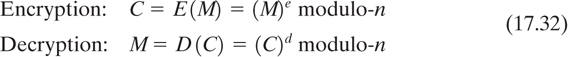
They are each easy to compute and the results of each operation are integers in the range (0, n - 1). In the RSA scheme, n is obtained by selecting two large prime numbers p and q and multiplying them together:
Although n is made public, p and q are kept hidden, due to the great difficulty in factoring n. Then
called Euler’s totient function, is formed. The parameter ϕ(n) has the interesting property [12] that for any integer X in the range (0, n - 1) and any integer k,
Therefore, while all other arithmetic is done modulo-n, arithmetic in the exponent is done modulo-ϕ(n). A large integer, d, is randomly chosen so that it is relatively prime to ϕ(n), which means that (n) and d must have no common divisors other than 1, expressed as
where gcd means “greatest common divisor.” Any prime number greater than the larger of (p, q) will suffice. Then the integer e, where 0 < e < (n), is found from the relationship
which, from Equation (17.35), is tantamount to choosing e and d to satisfy
Therefore,
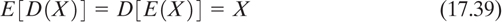
and decryption works correctly. Given an encryption key (n, e), one way that a cryptanalyst might attempt to break the cipher is to factor n into p and q, compute (n) = (p - 1)(q - 1), and compute d from Equation (17.37). This is all straightforward except for the factoring of n.
The RSA scheme is based on the fact that it is easy to generate two large prime numbers, p and q, and multiply them together, but it is very much more difficult to factor the result. The product can therefore be made public as part of the encryption key, without compromising the factors that would reveal the decryption key corresponding to the encryption key. By making each of the factors roughly 100 digits long, the multiplication can be done in a fraction of a second, but the exhaustive factoring of the result should take billions of years [2].
17.5.3.1 Use of the RSA Scheme
Using the example in Reference [13], let p = 47, q = 59. Therefore, n = pq = 2773 and ϕ(n) = (p - 1)(q - 1) = 2668. The parameter d is chosen to be relatively prime to ϕ(n). For example, choose d = 157. Next, the value of e is computed as follows (the details are shown in the next section):
Therefore, e = 17. Consider the plaintext example
ITS ALL GREEK TO ME
By replacing each letter with a two-digit number in the range (01, 26) corresponding to its position in the alphabet, and encoding a blank as 00, the plaintext message can be written as
0920 1900 0112 1200 0718 0505 1100 2015 0013 0500
Each message needs to be expressed as an integer in the range (0, n -1); therefore, for this example, encryption can be performed on blocks of four digits at a time since this is the maximum number of digits that will always yield a number less than n - 1 = 2772. The first four digits (0920) of the plaintext are encrypted as follows:
C = (M)e modulo-n = (920)17 modulo-2773 = 948
Continuing this process for the remaining plaintext digits, we get
C = 0948 2342 1084 1444 2663 2390 0778 0774 0219 1655
The plaintext is returned by applying the decryption key, as follows:
M = (C)157modulo-2773
17.5.3.2 How to Compute e
A variation of Euclid’s algorithm [14] for computing the gcd of ϕ(n) and d is used to compute e. First, compute a series x0, x1, x2, . . . , where x0 = ϕ(n), x1 = d, and xi + 1 = xi − 1 modulo-xi, until an xk = 0 is found. Then the gcd (x0, x1) = xk − 1. For each xi compute numbers ai and bi such that xi = ai x0 + bix1. If xk − 1 = 1, then bk − 1 is the multiplicative inverse of x1 modulo-x0. If bk − 1 is a negative number, the solution is bk − 1 + ϕ(n).
EXAMPLE 17.5 COMPUTATION OF E FROM D AND (N)
For the previous example, with p = 47, q = 59, n = 2773, (n) = 2688, and d chosen to be 157, use the Euclid algorithm to verify that e = 17.
Solution
i |
xi |
ai |
bi |
yi |
|---|---|---|---|---|
0 |
2668 |
1 |
0 |
|
1 |
157 |
0 |
1 |
16 |
2 |
156 |
1 |
–16 |
1 |
3 |
1 |
–1 |
17 |
where
Hence
e = b3 = 17
17.5.4 The Knapsack Problem
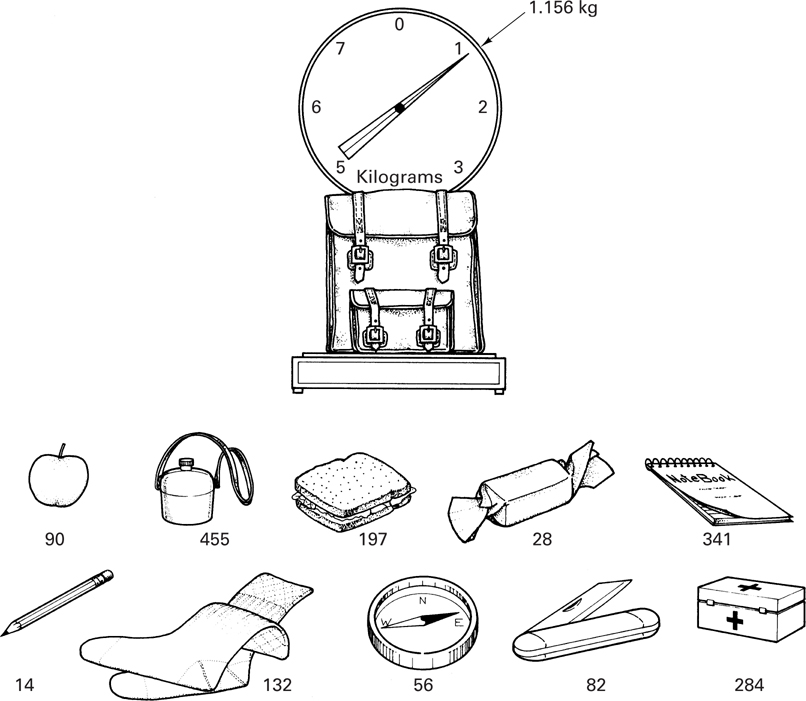
The classic knapsack problem is illustrated in Figure 17.19. The knapsack is filled with a subset of the items shown with weights indicated in grams. Given the weight of the filled knapsack (the scale is calibrated to deduct the weight of the empty knapsack), determine which items are contained in the knapsack. For this simple example, the solution can easily be found by trial and error. However, if there are 100 possible items in the set instead of 10, the problem may become computationally infeasible.
)
Let us express the knapsack problem in terms of a knapsack vector and a data vector. The knapsack vector is an n-tuple of distinct integers (analogous to the set of possible knapsack items)
a = a1, a2, … , an
The data vector is an n-tuple of binary symbols
x = x1, x2, … , xn
The knapsack, S, is the sum of a subset of the components of the knapsack vector:
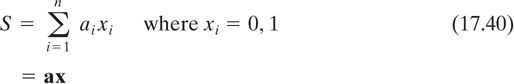
The knapsack problem can be stated as follows: Given S and knowing a, determine x.
EXAMPLE 17.6 KNAPSACK EXAMPLE
Given a = 1, 2, 4, 8, 16, 32 and S = ax = 26, find x.
Solution
In this example x is seen to be the binary representation of S. The decimal-to-binary conversion should appear more familiar with a expressed as 20, 21, 22, 23, 24, 25. The data vector x is easily found since a in this example is super-increasing, which means that each component of the n-tuple a is larger than the sum of the preceding components. That is,
When a is super-increasing, the solution of x is found by starting with xn = 1 if S ≥ an (otherwise xn = 0) and continuing according to the relationship
where i = n − 1, n − 2, . . . , 1. From Equation (17.42) it is easy to compute x = 0 1 0 1 1 0.
17.5.5 A Public Key Cryptosystem Based on a Trapdoor Knapsack
This scheme, also known as the Merkle–Hellman scheme [15], is based on the formation of a knapsack vector that is not super-increasing and is therefore not easy to solve. However, an essential part of this knapsack is a trapdoor that enables the authorized user to solve it.
First, we form a super-increasing n-tuple a′. Then we select a prime number M such that
We also select a random number W, where 1 < W < M, and we form W−1 to satisfy the following relationship:
the vector a′ and the numbers M, W, and W−1 are all kept hidden. Next, we form a with the elements from a′, as follows:
The formation of a using Equation (17.45) constitutes forming a knapsack vector with a trapdoor. When a data vector x is to be transmitted, we multiply x by a, yielding the number S, which is sent on the public channel. Using Equation (17.45), S can be written as follows:
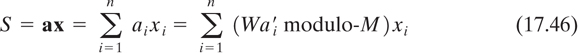
The authorized user receives S and, using Equation (17.44), converts it to S′:
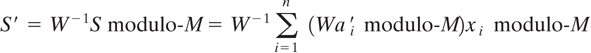
Since the authorized user knows the secretly held super-increasing vector a′, he or she can use S′ to find x.
17.5.5.1 Use of the Merkle–Hellman Scheme
Suppose that user A wants to construct public and private encryption functions. He first considers the super-increasing vector a′ = (171, 197, 459, 1191, 2410, 4517)
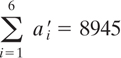
He then chooses a prime number M larger than 8945, a random number W, where 1 ≤ W < M, and calculates W−1 to satisfy WW−1 = 1 modulo-M.
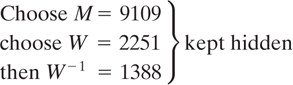
He then forms the trapdoor knapsack vector as follows:
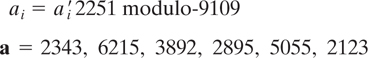
User A makes public the vector a, which is clearly not super-increasing. Suppose that user B wants to send a message to user A.
If x = 0 1 0 1 1 0 is the message to be transmitted, user B forms
S = ax = 14,165 and transmits it to user A
User A, who receives S, converts it to S′:
Using S′ = 3798 and the super-increasing vector a′ , user A easily solves for x.
The Merkle–Hellman scheme is now considered broken [16], leaving the RSA scheme (as well as others discussed later) as the algorithms that are useful for implementing public key cryptosystems.