17.4 Stream Encryption
Earlier, we defined a one-time pad as an encryption system with a random key, used one time only, that exhibits unconditional security. One can conceptualize a stream encryption implementation of a one-time pad using a truly random key stream (the key sequence never repeats). Thus, perfect secrecy can be achieved for an infinite number of messages, since each message would be encrypted with a different portion of the random key stream. The development of stream encryption schemes represents an attempt to emulate the one-time pad. Great emphasis was placed on generating key streams that appeared to be random, yet could easily be implemented for decryption, because they could be generated by algorithms. Such stream encryption techniques use pseudorandom (PN) sequences, which derive their name from the fact that they appear random to the casual observer; binary
pseudorandom sequences have statistical properties similar to the random flipping of a fair coin. However, the sequences, of course, are deterministic (see Section12.2). These techniques are popular because the encryption and decryption algorithms are readily implemented with feedback shift registers. At first glance it may appear that a PN key stream can provide the same security as the one-time pad, since the period of the sequence generated by a maximum-length linear shift register is 2n - 1 bits, where n is the number of stages in the register. If the PN sequence were implemented with a 50-stage register and a 1-MHz clock rate, the sequence would repeat every 250 - 1 microseconds, or every 35 years. In this era of large-scale integrated (LSI) circuits, it is just as easy to provide an implementation with 100 stages, in which case the sequence would repeat every 4 × 1016 years. Therefore, one might suppose that since the PN sequence does not repeat itself for such a long time, it would appear truly random and yield perfect secrecy. There is one important difference between the PN sequence and a truly random sequence used by a one-time pad. The PN sequence is generated by an algorithm; thus, knowing the algorithm, one knows the entire sequence. In Section 17.4.2 we will see that an encryption scheme that uses a linear feedback shift register in this way is very vulnerable to a known plaintext attack.
17.4.1 Example of Key Generation Using a Linear Feedback Shift Register
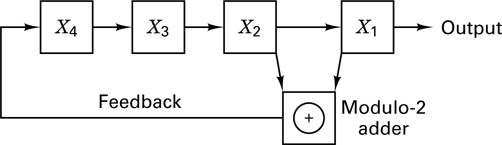
Stream encryption techniques generally employ shift registers for generating their PN key sequence. A shift register can be converted into a pseudorandom sequence generator by including a feedback loop that computes a new term for the first stage based on the previous n terms. The register is said to be linear if the numerical operation in the feedback path is linear. The PN generator example from Section 12.2 is repeated in Figure 17.13. For this example, it is convenient to number the stages as shown in Figure 17.13, where n = 4 and the outputs from stages 1 and 2 are modulo-2 added (linear operation) and fed back to stage 4. If the initial state of stages (x4, x3, x2, x1) is 1 0 0 0, the succession of states triggered by clock pulses would be 1 0 0 0, 0 1 0 0, 0 0 1 0, 1 0 0 1, 1 1 0 0, and so on. The output sequence is made up of the bits shifted out from the rightmost stage of the register, that is, 1 1 1 1 0 1 0 1 1 0 0 1 0 0 0, where the rightmost bit in this sequence is the earliest output and the leftmost bit is the most recent output. Given any linear feedback shift register of degree n, the output sequence is ultimately periodic.
17.4.2 Vulnerabilities of Linear Feedback Shift Registers
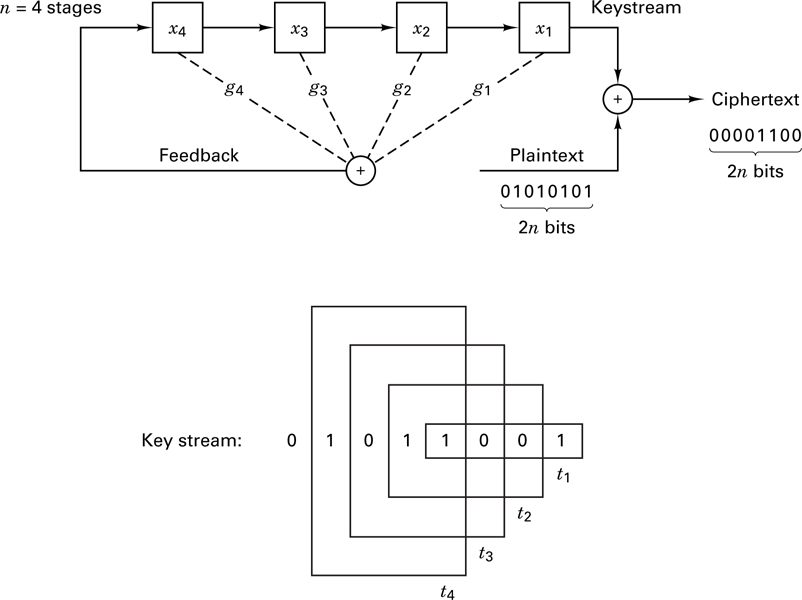
An encryption scheme that uses a linear feedback shift register (LFSR) to generate the key stream is very vulnerable to attack. A cryptanalyst needs only 2n bits of plaintext and its corresponding ciphertext to determine the feedback taps, the initial state of the register, and the entire sequence of the code. In general, 2n is very small compared with the period 2n − 1. Let us illustrate this vulnerability with the LFSR example illustrated in Figure 17.13. Imagine that a cryptanalyst who knows nothing about the internal connections of the LFSR manages to obtain 2n = 8 bits of ciphertext and its plaintext equivalent:
Plaintext: 0 1 0 1 0 1 0 1
Ciphertext: 0 0 0 0 1 1 0 0
where the rightmost bit is the earliest received and the leftmost bit is the most recent that was received.
The cryptanalyst adds the two sequences together, modulo-2, to obtain the segment of the key stream, 0 1 0 1 1 0 0 1, illustrated in Figure 17.14. The key stream sequence shows the contents of the LFSR stages at various times. The rightmost border surrounding four of the key bits shows the contents of the shift register at time t1. As we successively slide the “moving” border one digit to the left, we see the shift register contents at times t2, t3, t4,.... From the linear structure of the four-stage shift register, we can write
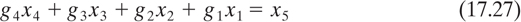
where x5 is the digit fed back to the input and gi (= 1 or 0) defines the ith feedback connection. For this example, we can thus write the following four equations with four unknowns, by examining the contents of the shift register at the four times shown in Figure 17.14:
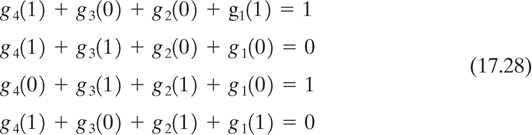
The solution of Equations (17.28) is g1 = 1, g2 = 1, g3 = 0, g4 = 0, corresponding to the LFSR shown in Figure 17.13. The cryptanalyst has thus learned the connections of the LFSR, together with the starting state of the register at time t1. He can therefore know the sequence for all time [3]. To generalize this example for any n-stage LFSR, we rewrite Equation (17.27) as follows:

We can write Equation (17.29) as the matrix equation

where
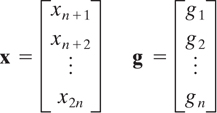
and
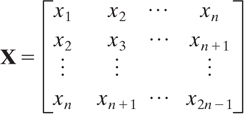
It can be shown [3] that the columns of X are linearly independent; thus X is non-singular (its determinant is nonzero) and has an inverse. Hence,

The matrix inversion requires at most on the order of n3 operations and is thus easily accomplished by computer for any reasonable value of n. For example, if n = 100, n3 = 106, and a computer with a 1- μs operation cycle would require 1 s for the inversion. The weakness of a LFSR is caused by the linearity of Equation (17.31). The use of nonlinear feedback in the shift register makes the cryptanalyst’s task much more difficult, if not computationally intractable.
17.4.3 Synchronous and Self-Synchronous Stream Encryption Systems
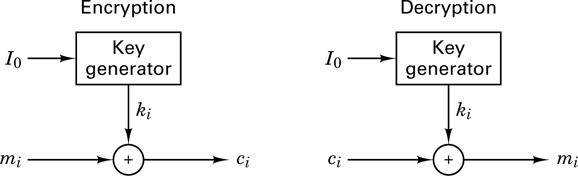
We can categorize stream encryption systems as either synchronous of self-synchronous. In the former, the key stream is generated independently of the message, so that a lost character during transmission necessitates a resynchronization of the transmission and receiver key generators. A synchronous stream cipher is shown in Figure 17.15. The starting state of the key generator is initialized with a known input, I0. The ciphertext is obtained by the modulo addition of the ith key character, ki, with the ith message character, m i. Such synchronous ciphers are generally designed to utilize confusion (see Section 17.3.1) but not diffusion. That is, the encryption of a character is not diffused over some block length of message. For this reason, synchronous stream ciphers do not exhibit error propagation.
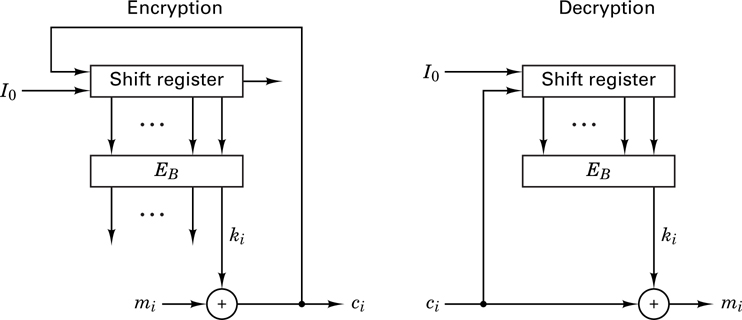
In a self-synchronous stream cipher, each key character is derived from a fixed number, n, of the preceding ciphertext characters, giving rise to the name cipher feedback. In such a system, if a ciphertext character is lost during transmission, the error propagates forward for n characters, but the system resynchronizes itself after n correct ciphertext characters are received.
In Section 17.1.4 we looked at an example of cipher feedback in the Vigenere auto key cipher. We saw that the advantages of such a system are that (1) a nonrepeating key is generated, and (2) the statistics of the plaintext message are diffused throughout the ciphertext. However, the fact that the key was exposed in the ciphertext was a basic weakness. This problem can be eliminated by passing the ciphertext characters through a nonlinear block cipher to obtain the key characters. Figure 17.16 illustrates a shift register key generator operating in the cipher feedback mode. Each output ciphertext character, ci (formed by the modulo addition of the message character, mi, and the key character, ki), is fed back to the input of the shift register. As before, initialization is provided by a known input, I0. At each iteration, the output of the shift register is used as input to a (nonlinear) block encryption algorithm EB. The low-order output character from EB becomes the next key character, ki + 1, to be used with the next message character, mi + 1. Since, after the first few iterations, the input to the algorithm depends only on the ciphertext, the system is self-synchronizing.